Chapter 3. Discrete Random Variables and Their Probability Distributions

[Mathematical Statistics with Applications 7th Edition, Wackerly, Mendenhall, Scheaffer]

이산확률변수와 이산확률분포

3.1 Basic Definition

확률변수(random variable) $Y$는 유한하거나, 셀 수 있는 무한한 개별로 나타낼 수 있으면 discrete(이산 변수)라고 한다.

 

 

3.2 The Probability Distribution for a Discrete Random Variable

$y$일 때의 $Y$의 확률은 $P(Y=y)$로 표기하고, 표본공간 $S$의 확률의 합으로 정의한다.

$P(Y=y)$는 $p(y)$로 표기하기도 한다

$Y$의 확률 분포는 공식, 표, 그래프로 표현할 수 있다.

Example 3.1

공장에 3명의 남자와 3명의 여자 근로자가 있다. 감독관은 2명의 근로자를 뽑아 특별한 작업을 하려고 한다. 감독관은 random하게 2명의 근로자를 선택하려고 한다. $Y$가 감독관이 뽑은 근로자의 여자 근로자 수라고 할 때, $Y$의 확률 분포를 구하라.

Solution

6명 중에서 2명을 뽑는 경우의 수는 $C^{6}_{2}=15$이다. 따라서 15개의 표본이 있고, 이 표본들은 균등한 기댓값을 갖는다. 

여성이 0명인 경우 $p(0) = P(Y = 0) = \frac{C^6_0 C^3_2}{15} = \frac{3}{15} = \frac{1}{5}$

여성이 1명인 경우 $p(1) = \frac{3}{5}$

여성이 2명인 경우 $p(2) = \frac{1}{5}$

 

확률분포를 표, 히스토그램으로 나타내면 다음과 같다

그리고 공식으로 나타내면 $p(y) = \frac{C^3_{y} C^3_{2-y}}{C^6_2}$

풀이 끝

 

모든 이산 확률 분포(discrete probability distribution)에서 다음과 같은 성질을 만족한다

1) $0 \leq p(y) \leq 1$ for all $y$

2) $\sum_{y} p(y) = 1$

 

3.3 The Expected Value of a Random Variable or a Function of a Random Variable

확률변수 $Y$의 확률 함수를 $p(y)$라 하자. 이때 $Y$의 기댓값(expected value)을 $E(Y)$라 하고 다음과 같이 정의한다.

$$E(Y) = \sum_{y}yp(y)$$

$p(y)$가 모집단의 빈도 분포를 나타낸다면, $E(Y)=\mu$라고 하고 모평균(population mean)이라 한다.

 

확률변수 $Y$가 이산확률변수고, 확률함수를 $p(y)$, 그리고 실수 함수 $g(Y)$가 있다고 하자. 이때  $g(Y)$

의 기댓값은 다음과 같이 계산한다.

$$ E[g(Y)] = \sum_{y}g(y)p(y)$$

 

확률변수 $Y$에 대하여 평균이 $E(Y) = \mu$일 때, 분산은 $(Y - \mu)^2$의 평균으로 정의한다. 즉

$$V(Y) = E[(Y - \mu)^2] = \sigma^2$$

Example 3.2

다음 표과 같이 확률변수 $Y$가 정의되어있을때, $Y$의 평균, 분산, 표준편차를 구하라.

Solution

$\mu = E(Y) = (0)(1/8) + (1)(1/4) + (2)(3/8) + (3)(1/4) = 1.75$

$\sigma^2 = (0 - 1.75)^2 (1/8) + (1 - 1.75)^2(1/4) + (2 - 1.75)^2(3/8) + (3 - 1.75)^2(1/4) = .935$

$\sigma = \sqrt{.9375} = .97$

풀이 끝

 

확률변수 $Y$, 확률함수 $p(y), g(Y)$에 대하여 다음이 성립한다

1) $E(c) = c$, $c$는 상수

2) $E[cg(Y)] = cE[g(Y)]$

3) $E[g_1(Y) + g_2(Y)] = E[g_1(Y)] + E[g_2(Y)]$

 

그리고 확률변수 $Y$, 확률함수 $p(y)$, 평균 $E(Y)=\mu$에 대하여 다음이 성립한다

$$V(X) = \sigma^2 = E(Y^2) - \mu^2$$

 

Example 3.3

공장 매니저는 2개의 새 타입($A, B$)의 기계를 사려고 한다. $t$가 하루 가동 시간(hour), $Y_1$이 기계 A의 하루 수리 횟수, $Y_2$가 기계 B의 하루 수리 횟수라 하고 각각 평균과 분산이 $.10t, .12t$이다. 하루 총 비용은 A. B 각각

$C_A(t) = 10t + 30Y_1^2$

$C_B(t) = 8t + 30Y_2^2$

각 경우가 비용의 기댓값이 작은 기계는?

(a) 10시간

(b) 20시간

Solution

분산 공식에서 $E(Y^2) = V(Y) + E(Y)^2$을 이용한다.

$E[C_A(t)] = E[10t + 30Y_1^2] = 10t + 30{V(Y_1) + E(Y_1)^2} = 10t + 30{.10t + (.10t)^2} = 13t + .3t^2$

$E[C_B(t) = 11.6t + .432t^2$

 

$t=10$일 때는 B가, $t=20$일 때에는 A가 더 비용이 적다.

풀이 끝

 

 

3.4 The Binomial Probability Distribution

이항 실행(binomial experiment)는 다음과 같은 성질을 갖는다

1) 각 실행은 고정된 수 $n$으로 이루어져있고 각 시행이다.

2) 각 시행은 2개의 결과를 갖는다; 성공과 실패($S, F$)

3) 각 시행마다 성공할 확률을 동일하다. 성공/실패할 확률을 $p, q$라 하고, $q = 1 - p$이다

4) 각 시행은 독립이다

5) 확률변수 $Y$는 시행 중 성공한 횟수이다.

 

확률변수 $Y$는 성공확률이 $p$이고 $n$번의 시행을 할 때 이항분포(binomial distribution)이고, 공식은 다음과 같다

$$p(y) = C^n_y=p^yq^{n - y}, y = 0, 1, 2, ..., n$$

그리고 $\mu = E(Y) = np, \sigma^2 = V(Y) = npq$ 이다.

 

 

 

Example 3.10

20명의 설문조사를 통해 새로운 퇴직금 정책에 우호적인지 조사하였다. 우리의 표본에서 6명이 우호적이라 했을 때, 확률 $p$를 구하시오.

Solution

$P(Y = 6) = C^{20}_{6}p^6(1 - p)^{14}$이고, $P(Y = 6)$을 최대화 하자.

양변에 로그를 합성하면

$$\ln(P) = 6\ln(p) + 14\ln(1 - p)$$

$$d\frac{6\ln(p) + 14\ln(1 - p)}{dp} = \frac{6}{p} - \frac{14}{1 - p}$$

위 식이 $0$이 되는 $p$는 $p = 6/20$

(이 풀이 방법은 9장에서 최대우도법(maximum likelihood estimation)을 이용한 것이다)

풀이 끝

 

3.5 The Geometric Probability Distribution

기하분포를 따르는 확률변수는 이항분포와 몇가지 특징을 공유한다. 성공확률 $p$는 시행마다 변하지 않는다. 하지만 기하분포에서느 확률변수 $Y$는 첫번째 성공이 일어날때까지의 시행 횟수로 정의한다. (이항분포와 정의가 다르다!)

$p(y) = P(Y = y) = P(E_y) = P(FFFFF...FS) = qqq \dots qp = q^{y - 1}p$. $0 \le p \le 1$

$p=.5$일 때 기하분포

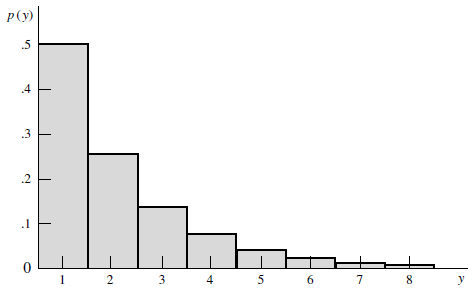
기하분포는 대기시간의 길이 분포에 자주 사용된다. 

Example 3.11

엔진이 한시간동안 오작동할 확률이 $p.2$라고 한다. 이때, 엔진이 2시간 동작할 확률을 구하시오.

Solution

$Y$가 첫 오작동때까지 한시간 구간의 개수라 하자. 구해야하는 건

$$P(Y \ge 3) = \sum_{y=3}^{\infty}p(y) = 1 - \sum_{y = 1}^{2}p(y) = 1 - {p + qp} = .9604$$

풀이 끝.

 

기하분포의 평균과 분산은$\mu = \frac{1}{p}, \sigma^2 = \frac{1 - p}{p^2}$이다.

 

Example 3.13

3.10번에서 한 인터뷰를 연속적으로 시행하고, 처음으로 긍정적으로 인터뷰한 사람에서 인터뷰를 멈추려고 한다. 만약 5번째 사람이 처음으로 긍적적으로 답한 사람이라면, p를 예측해보라.

Solution

$P(Y = 5) = (1 - p)^4p$이고 로그를 씌우로 $p$에 대하여 미분하여 $0$이 되는 $p$를 구하면 $p = 1/5$이다.

 

풀이 끝.

 

3.6 The Negative Binomial Probability Distribution

음이항분포. 기하분포를 조금 확장하여 $n$번의 시행 동안 2번, 3번, ..., $r$번 성공할 확률은?

즉 $n$번 시행하여 $r$번 성공할 확률의 분포를 음이항분포라 한다.

$$p(y) = C^{y - 1}_{r - 1}p^{r}q^{y - r}, y = r, r + 1, r + 2, ..., 0 \le p \le 1$$

$$\mu = \frac{r}{p}, \sigma^2 = \frac{r(1 - p)}{p^2}$$

 

Example 3.15

펌프 재고창고에서 20% 정도는 수리가 필요하다고 한다. 유지보수 근로자는 3개의 수리키트를 보내려고 한다. 근로자는 임의로 펌프를 고르고 한번에 테스트를 한다. 만약 펌프가 동작하면 나중에 사용하기 위해 따로 보관한다. 만약 펌프가 동작하지 않으면, 그녀는 수리키트를 사용한다. 

정상펌프를 테스트하는데 10분이 걸리고, 고장난 펌프를 테스트하는데는 수리시간을 포함하여 30분이 걸린다고 하자. 3개의 수리키트를 사용하는데 소요되는 시간의 평균과 분산을 구하라.

Solution

$Y$를 3번 고장난 펌프를 찾는 시행횟수라 하면 $Y$는 $r = 3, p = .2$인 음이항분포를 따른다.

즉 $E(Y) = 3 / (0.2) = 15, V(Y) = 60$이다. 고장난 펌프는 20분의 수리시간이 더 덜기 때문에 전체 시간은 $T = 10Y + 3(20)$이므로 $E(T) = 210, V(T) = 6000$이다.

풀이 끝.

3.7 The Hypergeometric Probability Distribution

초기하분포

(표본공간에는 2가지의 표본만 존재한다)

전체 표본 개수가 $N$, 추출할 표본 개수를 $n$, 타겟 표본의 전체 개수를 $r$, 뽑을 타겟 표본의 개수를 $y$라 하면

$$p(y) = \frac{C^{r}_{y} C^{N - r}_{n - y}}{C^{N}_{n}}$$

$$\mu = \cfrac{nr}{N}, \sigma^2 = n\left(\cfrac{r}{N}\right) \left(\cfrac{N - r}{N}\right) \left(\cfrac{N - n}{N - 1}\right) = npq\left(\frac{N - n}{N - 1}\right)$$

3.8 The Poisson Probability Distribution

포아송 분포(푸아송 분포)

일주일 동안 자동차 사고의 횟수의 확률분포를 알아보자. 먼저 구간(일주일)을 작은 구간(subinterval)으로 쪼개서 해당 구간에는 사고가 딱 한번(혹은 0번) 발생할 수 있다고 하자. subinterval에서 2번 이상 사고가 날 확률은 $0$이고, 1번 사고가 날 확률은 $p$, 사고가 일어나지 않을 확률은 $q(= 1 - p)$이다. 이제 작은 구간들의 합을 구하면 우리가 구하고자 하는 사고 횟수의 확률분포가 된다. $\lambda = np$라 하고 작은 구간을 한없이 작게 해야하므로 이 식을 유도하면

포아송 분포 유도

$$p(y) = \cfrac{\lambda^y}{y!}e^{-\lambda}, \mu = \lambda, \sigma^2 = \lambda$$

Example 3.22

한달에 3번 발생하고 포아송 과정을 따르는 산업재해가 있다. 지난 2달 동안 재해는 10번 발생했다.

만약 한달 평균 사고 발생 횟수가 3($\mu$)이라면 이는 평균보다 많이 발생한 것인가? 

Solution

2달동안 사고가 발생했으므로 $\lambda^* = (2)(3) = 6$이므로 $Y$가 $10$이상일 확률은

$$P(Y \ge 10) = \sum_{y=10}^{\infty}\cfrac{6^{y} e^{-6}}{y!}$$

(표, 프로그램을 이용하면) $Y$는 구간 $\mu \pm 2\sigma$에 있을 확률이 높다. $\mu + 2\sigma = 10.90$이므로 $Y = 10$에 있는 것은 경계에 있다. 이런 일이 일어날 확률이 아주 높은 것은 아니지만 충분히 발생할 수 있다고 판단할 수 있다.

3.9 The Moments and Moment-Generating Functions

적률, 적률생성함수

모수 $\mu, \sigma$는 확률변수의 중심과 흩어진 정도(산포도)를 잘 설명해준다.