[Mathematical Statistics with Applications 7th Edition, Wackerly, Mendenhall, Scheaffer]
통계적 추정
8.1 Introduction
관심있는 파라미터를 target parameter라고 부르고, 이는 $p, \mu, \sigma^2$ 등이 될 수 있다.
point estimate(점추정): 단일 값, 단일 점에 대한 추정(예. $\mu$)
interval estimate(구간추정): 구간에 대한 추정 ($(.07, .19)$)
estimator(추정량): 추정값에 대한 공식이나 표현
표본평균(sample mean, $\bar{Y} = \cfrac{1}{n} \sum_{i = 1}^{n}Y_i$)은 estimator의 한 예이다.
같은 모수를 추정할 때에 다른 estimator를 활용할 수 있으며, 좋을 수도, 나쁠 수도 있다.
8.2 The Bias and Mean Square Error of Point Estimators
점추정은 리볼버로 과녁을 맞추는 것에 비유할 수 있다. 사격수가 한발을 과녁에 발사했다고 하자. 그것이 좋은 발사였는가? 만약에 100발을 과녁에 맞았다면, 사격수가 다음에 좋은 사격을 할 지 알수 있을 것이다.
즉, 우리는 점추정을 할 때 단번의 추정으로는 그 추정량이 좋은지 나쁜지 알 수 없다. 그렇기 때문에 수많은 추정을 해야 한다.
우리가 모수 $\theta$를 점추정을 하고 싶다고 하자. 그 추정량은 $\hat{\theta}$이고 세타 햇으로 읽는다. 리볼버 사격에서, 표본들이 그림8.1처럼 분포되기를 원한다. 즉 $E(\hat{\theta}) = \theta$ 인 것이다. 점추정이 이를 만족하면 우리는 unbiased 라고 부른다. 만약 표본 분포가 biased되어 $E(\hat{\theta}) > \theta$ 라면 그림 8.2처럼 될 것이다.

$\hat{\theta}$가 $\theta$의 점추정량이라 하자. $E(\hat{\theta}) = \theta$를 만족하면 $\hat{\theta}$은 불편추정량(unbiased estimator)라 하고, $E(\hat{\theta}) \neq \theta$라면 $\hat{\theta}$는 편의추정량(biased)라고 한다.
$\hat{\theta}$의 bias는 $B(\hat{\theta}) = E(\hat{\theta}) - \theta$ 이다.
우리는 분산이 작으면 $\hat{\theta}$가 $\theta$에 가까울 것임을 보장할 수 있다. 즉 $V(\hat{\theta})$가 작기를 원한다. 우리는 가능한 작은 분산을 가진 불편추정량을 고를 것이다.
분산을 직접 계산하는 대신에, 우리는 $E(\hat{\theta} - \theta)^2$를 이용하고 mean square error라 부른다. 즉 $MSE(\hat{\theta}) = V(\hat{\theta}) + [ B(\hat{\theta})]^2$이다.
8.3 Some Common Unbiased Point Estimators
대표적인 불편추정량들을 알아보자

표본분산($S^2$)의 기댓값이 모분산($\sigma^2$)이 되어야 함을 이용하여 표본분산의 불편추정량이
$$S^2 = \cfrac{1}{n-1} \sum_{i=1}^{n}(Y_i - \bar{Y})^2$$
임을 알 수 있다.
위에 적힌 4가지 parameter들은 large sample인 경우에 정규분포를 따른다.(중심극한정리) 일반적으로 $n=30$이상이면 충분이 큰 표본(large samples)이라 한다.
8.4 Evaluating the Goodness of a Point Estimator
점추정을 평가하는 법
error of estimation: $\epsilon = |\hat{\theta} - \theta|$
error bound: $P(|\hat{\theta} - \theta|) < b = 0.90$

Example 8.2
표본의 크기가 $n=1000$인 유권자들 중에서 $560$명이 후보 Jones에게 투표했다고 한다. Jones에게 투표한 비율 $p$를 추정하고, 2-standard-error bound를 구하라.
표본의 크기가 충분히 크기 때문에 표본비율을 사용한다.
$\hat{p} = 560/1000 = 0.56, b = 2\sigma_{\hat{p}}=2\sqrt{\cfrac{pq}{n}} \approx 2\sqrt{\cfrac{(0.56)(0.44)}{1000}} = 0.03$
추정량 $.56$은 $.03$ 오차 이내에 모비율 $p$가 있다고 확신할 수 있다.
Example 8.3
두 종류의 자동차 타이어의 내구도를 비교하려고 한다. $n_1 = n_2 = 100$의 표본을 구했다. 두 타이어는 독립적으로 기록했고 다음과 같은 평균과 분산을 구하였다.
$$\bar{y_1} = 26,400, \quad \bar{y_2} = 25,100$$
$$s_1^2 = 1,440,000, \quad s_2^2 = 1,960,000$$
2-standard-error 오차범위에서 평균의 차이를 추정하여라.
$\bar{y_1} - \bar{y_2} = 1300$
$\sigma_{\left(\bar{Y_1} - \bar{Y_2}\right)} = \sqrt{\cfrac{\sigma_1^2}{n_1} - \cfrac{\sigma_2^2}{n_2}}$
하지만 모표준편차(와 모분산)를 구할 수 있는 방법은 없다. 대신 모분산의 불편추정량을 이용하여
$$\sigma_i^2 = S_i^2 = \cfrac{1}{n_i - 1} \sum_{j=1}^{n_i} \left(Y_{ij} - \bar{Y_{i}}\right)^2, \quad i=1, 2$$
따라서
$$\sigma_{\left(\bar{Y_1} - \bar{Y_2}\right)} = \sqrt{\cfrac{\sigma_1^2}{n_1} - \cfrac{\sigma_2^2}{n_2}} \approx \sqrt{\cfrac{s_1^2}{n_1} + \cfrac{s_2^2}{n_2}} = \sqrt{34,000}=184.4$$
따라서, 차의 평균은 1300으로 추정하고, 184.4 사이에 있을 확률은 95%이다.
8.5 Confidence Intervals
신뢰구간
이상적으로, 2가지 성질은 갖는다. target parameter $\theta$를 가지면서 상대적으로 좁아햐 한다. 우리의 목표는 높은 확률로 $\theta$를 포함하면서 좁은 구간을 찾는 것이다.
신뢰구간의 하단과 상단을 각각 좌측신뢰한계(lower confidence limit), 우측신뢰한계(upper confidence limit)라 부른다. 그리고 신뢰구간이 $\theta$에 가까운 확률을 신뢰계수(confidence coefficient)라 부른다.
$\hat{\theta_L}$과 $\hat{\theta_U}$를 각각 좌/우측 신뢰한계라 하자. 그러면 $(1-\alpha)$가 신뢰 계수일 때
$$P(\hat{\theta_L} \le \hat{\theta_U}) = 1 - \alpha$$
인 $[\hat{\theta_L}, \hat{\theta_U}]$을 양방향신뢰구간(two-sided confidence interval)이라 부른다.
물론, 단방향 신뢰구간(one-sided confidence interval)도 존재한다.
신괴구간이 $[\hat{\theta_L}, \infty$인 경우에는 신뢰계수가 $P(\hat{\theta_L} \le \theta) = 1 - \alpha$이고,
신뢰구간이 $(-\infty, \hat{\theta_U}]$인 경우에는 신뢰계수가 $P(\theta \le \hat{\theta_U}) = 1 - \alpha$가 된다.
Example 8.4
평균이 $\theta$인 지수분포를 관찰한다고 하자. 신뢰계수가 $0.9$인 신뢰구간을 구하여라.
$Y$의 pdf가 $y$가 음수인 곳에서는 $0$이고 그 외에는 $f(y) = \cfrac{1}{\theta}e^{-y/\theta}$이다.
$U = Y/\theta$로 치환하면 누적함수는 $f_U(u) = e^{-u}$이다. 중심충략(pivotal method)의 성질에 따라 $P(a \le U \le b) = 0.9$인 $a, b$를 찾는 것과 동일한 문제로 치환되었다.
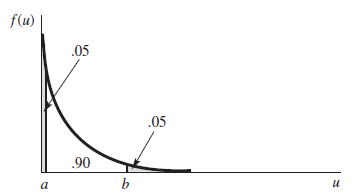
$P(U \le a) = \displaystyle\int_0^a e^{-u}du = 0.5, \quad 1 - e^{-a} = 0.5, \quad a = 0.051$
$P(U > b) = \displaystyle\int_{b}^{\infty}e^{-u}du = 0.5, \quad e^{-b}=0.5, \quad b = 2.996$
따라서 $0.90 = P(0.051 \le \cfrac{Y}{\theta} \le 2.996) = P(\cfrac{Y}{2.996} \le \theta \le \cfrac{Y}{0.051})$
8.6 Large-Scale Confidence Intervals
충분한 표본에서의 신뢰구간
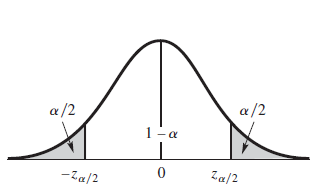
$\theta$가 $\mu, p, \mu_1 - \mu_2, p_1 - p_2$이면서 많은 표본을 가지고 있다면 $Z = \cfrac{\hat{\theta} - \theta}{\sigma_{\theta}}$는 정규분포에 근사하며 pivotal quantity이고 pivotal method를 적용하여 신뢰구간을 구할 수 있다.
Example 8.7
동네 슈퍼에서 사람들의 쇼핑시간을 추출하였고 ($n = 64$), 쇼핑시간의 평균과 분산은 각각 33(분)과 256(분$^2$)이다. 신뢰계수가 $1-\alpha = 0.90$일 때의 $\mu$를 추정하여라.
$\theta = \mu, \hat{\theta} = \bar{y} = 33, s^2 = 256$이고 $n > 30$이므로 $s^2$을 모분산($\sigma^2$)으로 대체한다.
정규분포표를 이용하면
$\bar{y} - z_{\alpha / 2}\left(\cfrac{s}{\sqrt{n}}\right) = 33 - 1.645\left(\cfrac{16}{8}\right) = 29.71$
$\bar{y} + z_{\alpha / 2}\left(\cfrac{s}{\sqrt{n}}\right) = 33 + 1.645\left(\cfrac{16}{8}\right) = 36.29$
따라서 구간 $(29.71, 36.39)$에 $\mu$가 있을 확률은 95%이다.
Example 8.8
두개의 냉장고 브랜드 A, B가 있다. A냉장고에서 50개의 표본을, B냉장고에서 60개의 표본을 추출하고 각각 12, 12개의 보증내 불량이 발견되었다. 98%의 신뢰계수를 갖는 $(p_1 - p_2)$를 추정하여라.
$$(\hat{p_1} - \hat{p_2}) \pm z_{\alpha / 2}\sqrt{\cfrac{p_1q_1}{n_1} + \cfrac{p_2q_2}{n_2}}$$
이고, $n$이 충분히 크기 때문에 모비율 대신에 표본비율을 이용할 수 있다.
$\hat{p_1} = 0.24, \hat{p_2} = 0.2$에서 $\hat{q_1} = 0.76, \hat{q_2} = 0.8$이므로 신뢰구간은 $[-0.1451, 0.2251]$이다.
8.7 Selecting the Sample Size
신뢰계수를 이용하여 특정 신뢰도를 확보하기 위한 표본 개수를 유추할 수 있다. 하지만 $\sigma$를 알 수 없기 때문에 $s^2$로 대체한다 하더라도 상당한 오차가 발생한다. 그럼에도 불구하고, 이 방법은 large-sample estimation에서는 유효하다.
$$P(Z > z_{\alpha / 2}) = \cfrac{\alpha}{2}$$
Example 8.9 (변형)
어떤 심리 실험에 따르면 두개의 결과를 알 수 있다고 한다. $p$는 긍정적인 반응을 일으키는 확률이라 하자. 얼마나 많은 사람들을 실험에 참여해야하는가? 추정량의 오차는 $0.04$ 이하이어야 하고 신뢰도는 90%와 같아댜한다.
$1 - \alpha = 0.9$이므로 $\alpha = 0.1$, $\alpha / 2 = 0.05$이다.
표준정규분포를 이용하면 $z_{\alpha / 2}=1.645$이므로 $1.645\cfrac{pq}{n} = 0.04$인 $n$을 구한다.
$p$를 알 수 없기 때문에 maximum possible value인 $p=0.5$로 하고 계산하면 $n=423$이다.
추정된 $n$이 충분히 크기 때문에 $B = 0.04$이면서 신뢰도 90%를 유지하는데 무리가 없다.
8.8 Small-Sample Confidence Intervlas for $\mu$ and $\mu_1 - \mu_2$
적은 표본에서의 모평균의 신뢰구간과 모평균의 차의 신뢰구간
$Y_1, Y_2, ..., Y_n$가 정규분포에서 추출된 확률변수일 때 $\bar{Y}$와 $S^2$는 표본평균(sample mean)과 표본분산(sample variance)이다. 이때 확률변수 $T$는
$$T = \cfrac{\bar{Y} - \mu}{S / \sqrt{n}}$$
이고 자유도가 $(n-1)$인 t분포를 따른다. 따라서 신뢰구간은 다음과 같이 구한다.
$$P(-t_{\alpha / 2} \le T \le t_{\alpha / 2}) = 1 - \alpha$$
이때 \alpha는 자유도 $(n - 1)$임에 의존함을 주의한다.
모평균의 신뢰구간은 $\bar{Y} = t_{\alpha / 2}\left(\cfrac{S}{\sqrt{n}}\right)$로 구한다.
Example 8.11
한 화약 제조업체가 여덟 개의 껍데기에서 실험된 새로운 화약을 개발했다. 그 결과 초당 피트 단위의 총구 속도는 다음과 같았다고 한다.
$$3005, 2925, 2935, 2965, 2995, 3005, 2937, 2905$$
이때, 95%의 신뢰도를 갖는 $\mu$의 신뢰구간을 구하여라. 총구속도는 정규분포에 근사한다고 가정한다.
$\bar{y}=2959, s = 39.1, n - 1 = 7, \alpha=0.05$이므로 t분포표를 이용하면 $t_{0.025}=2.365$이다. 따라서 모평균 $\mu$의 신뢰구간은 $2959 \pm 32.7$이다.

8.9 Confidence Intervals for $\sigma^2$
모분산의 신뢰구간
$Y_1, Y_2, ..., Y_n$가 정규분포에서 추출된 확률변수이고 $\mu, \sigma^2$ 모두 알 수 없다고 하면 다음을 만족한다.
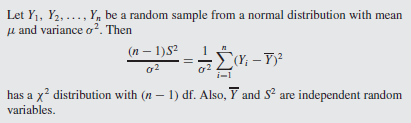
따라서 신뢰구간은
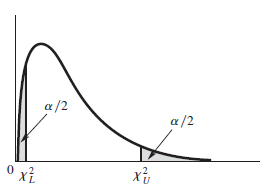
$$P\left[ \chi^2_L \le \cfrac{(n-1)S^2}{\sigma^2}\le \chi^2_U\right] = 1 - \alpha$$
카이제곱분포는 비대칭이므로 $\chi^2_L, \chi^2_U$를 구하는 것이 자유롭다. 우리는 가장 짧은 신뢰구간을 찾기를 원하기 때문에, 경험적으로 아래와 같이 좌측/우측신뢰한계를 구한다.

8.10 Summary
- $MSE(\hat{\theta}) = V(\hat{\theta}) + [ B(\hat{\theta})]^2$
- $n$이 충분히 크다면, CLT(중심극한정리)에 따라 $\mu, p$는 정규분포에 근사한다.
- $n$이 작고 표본이 정규분포를 따른다면, $\mu$의 신뢰구간을 구할때는 $t$분포를 이용한다.
- $n_1 \approx n_2$이고 정규분포를 따를때, $\mu_1 - \mu_2$의 신뢰구간을 구할 수 있다.
- 표본이 정규분포를 따르고 $\sigma^2$의 신뢰구간을 구할때는 카이제곱분포를 이용한다.
(3)과 (5)는 표본이 정규분포를 따르지 않는다면 보장할 수 없다
(4)에서 $n_1$과 $n_2$가 다를 수록, 분산은 치명적이다.
'스터디 > 확률과 통계' 카테고리의 다른 글
| [확률] 베이즈 정리 (Bayes' theorem) (0) | 2023.02.18 |
|---|---|
| Chapter 10. Hypothesis Testing (0) | 2022.08.24 |
| Chapter 9. Properties of Point Estimators and Methods of Estimation (0) | 2022.08.13 |
| Chapter 4. Continuous Variables and Their Probability Distributions (0) | 2022.07.30 |
| Chapter 3. Discrete Random Variables and Their Probability Distributions (0) | 2022.07.30 |



