[Mathematical Statistics with Applications 7th Edition, Wackerly, Mendenhall, Scheaffer]
가설검정
10.1 Introduction
가설검정(Hypothesis testing)은 관측에 반하는 이론을 검증하는 모든 영역에서 행해진다. 가설검정은 관찰된 표본과 이론을 비요하여 의사결정을 내리는 것을 요구한다. 어떤 경우에 가설을 폐기해야하는가? 수용한다면? 잘못된 결정을 내릴 확률은? 이러한 질문들에 대한 답을 배울 것이다.
10.2 Elements of a Statistical Test
가설검정의 요소
$H_0$: 귀무가설, Null hypothesis
$H_a$: 대립가설, Alternative hypothesis (책에 따라 $H_1$이라 표기하기도 한다)
검정 통계량(Test statistic): 통계적 결론에 기반한 표본에 대한 함수
기각역(Rejection region, RR): 귀무가설이 기각되고 대립가설이 채택되는 검정통계량의 값들
1종 오류(type I error): $H_0$가 참 일때 $H_0$가 기각됨. 1종오류가 일어날 확률을 $\alpha$라고 하며 level(유의수준)이라 부른다.
2종 오류(type II error): $H_a$가 참일때 $H_0$를 채택함. 2종오류가 일어날 확률을 $\beta$로 표기한다.
Example 10.1
$n=15$인 Jones의 여론조사를 실시했다. 우리는 $H_0: p=0.5$과 $H_a: p < 0.5$를 검정하려고 한다. 검정통계량은 $Y$이고 Jones에게 호의를 보인 사람들의 수이다. 기각역이 $\textrm{RR} = \{y \le 2\}$일 때, $\alpha$를 구하시오.
$\alpha = P(type I error) = P(Y \le 2$ when $p=0.5$ 이므로
$\alpha = \sum_{y=0}^{2}\binom{15}{y}(0.5)^{y}(0.5)^{15-y} = 0.004$
이는 우리가 정한 기각역 RR이 매우 적은 리스크(0.004)로 jones가 승자임에도 질 것이라고 예측할 리스크가 적다는 뜻이다.
Example 10.4
예제 10.1의 상황에서 기각역을 RR = {$y \le 5$}라고 하자. $p=0.3$일 때, $\alpha, \beta$의 값을 구하시오.
$\alpha = P(Y \le 5$ when $p=0.5 = \sum_{y=0}^{5}\binom{15}{y}(0.5)^{15} = 0.151$
$\beta= P(Y > 5$ when $p=0.3 = \sum_{y=6}^{15}\binom{15}{y}(0.3)^{y}(0.7)^{15-y} = 0.278$
예제를 보다시피, 기각역이 넓어지면 $\alpha$의 값은 증가하고 $\beta$는 감소한다.
어떻게 하면 $\alpha$와 $\beta$ 모두 감소할 수 있을까? 대부분의 통계 검정에서, $\alpha$는 작은 값으로 고정시키고, $\beta$의 값은 sample size가 커지면 작아진다.
10.3 Common Large-Sample Tests
$H_0: \theta = \theta_0$
$H_1: \theta > \theta_0$
검정 통계량: $Z = \cfrac{\hat{\theta} - \theta_0}{\sigma_{\hat{\theta}}}$
RR = {$z > z_{\alpha}$}
만일 $Z$가 표준정규분포의 upper-tail에 충분이 떨어져 있다면 $H_0$를 기각한다.
Example 10.5
한 대기업의 영업 담당 부사장은 영업 사원들이 15건(주당 계약건) 이하의 계약을 한다고 주장한다. (부사장은 이 숫자를 늘리고 싶어한다.) 그의 주장을 확인하기위해, $n=36$인 영업사원들을 랜덤 선택하고, 계약수를 기록하였다. 평균과 분산은 각각 17과 9였다. 부사장의 주장은 모순적인가? $\alpha = 0.5$에서 확인해보라.
부사장의 주장은 $H_a$이고 귀무가설과 대립가설을 작성해보면
$$H_0: \mu = 15, \quad \textrm{against} \quad H_a: \mu > 15$$
$\mu_{\bar{Y}} = \mu, \sigma_{\bar{Y}} = \sigma / \sqrt{n}$이므로 검정 통계량은 $Z = \cfrac{\bar{Y} - \mu_0}{\sigma / \sqrt{n}}$이다. 그리고 기각역은 RR = {$z > z_{0.05} = 1,645$}이다. 모분산은 알 수 없지만 $n=36$은 충분히 큰 수이므로 표본표준편차를 대체할 수 있다. 따라서 $z = \cfrac{17-15}{3/ \sqrt{36}} = 4$.
따라서 $Z$가 RR안에 있으므로 $H_0$를 기각한다. 즉, $\alpha = 0.05$에서는 부사장의 주장이 부정확하다는 근거로 충분하고, 주당계약건수는 15를 초과한다는 의미가 된다.
위에서는 upper-tail alternative의 경우만 보았지만, lower-tail alternative, two-tailed alternative도 존재한다.

Example 10.7
심리학 실험에서 남자와 여자에 대한 자극에 대한 반응시간을 조사했다. 독립 표본으로 50명의 남성과 50명의 여성이 실험에 참여했고 그 결과는 아래 표와 같다. $\alpha = 0.05$ 일때, 남성과 여성의 반응시간이 동일하다고 볼 수 있는가?

$\mu_1, \mu_2$를 각각 남성과 여성의 평균 반응 시간이라 하면 아래와 같이 가설을 세울 수 있다.
$$H_0: (\mu_1 - \mu_2) = 0, \quad H_a: (\mu_1 - \mu_2) \neq 0$$
그러므로 우리는 양측검정(two-sided alternative)을 할 것이다.
$n$이 충분히 크기 때문에 모분산 대신 표본분산을 이용할 것이고, $Z = \cfrac{(\bar{Y_1} - \bar{Y_2}) - (\mu_1 - \mu_2)}{\sqrt{\cfrac{\sigma_1^2}{n_1} + \cfrac{\sigma_2^2}{n_2} }}$
$z = \cfrac{3.6 - 3.8}{\sqrt{\cfrac{(0.18)^2}{50} + \cfrac{(0.14)^2}{50} }}= -2.5$ 이고 기각역은 {$|z| > z_{\alpha / 2} = z_{0.025} = 1.96$} 이므로 기각역에 포함되어 $H_0$를 기각한다. 따라서 우리는 남성과 여성이 반응시간이 다르다는 충분한 증거가 존재한다고 주장할 수 있다.
10.4 Calculating Type II Error Probabilityes and Finding the Sample Size for Z Tests
$\beta$를 계산하는 것은 어렵지만 10.3에서 전개된 검정을 이용하면 쉽다. Z-test를 이용하여 $\beta$와 sample size 모두 계산할 수 있다.
다시 $H_0: \theta = \theta_0, H_a: \theta > \theta_0$, RR = {\hat{\theta}>k}라고 하자. 이때 $\beta$는
$\beta = P(\hat{\theta}$is not in RR when $H_a$ is true) = $P(\hat{\theta} \le k | \theta = \theta_0) = P\left( \cfrac{\hat{\theta} - \theta_a}{\sigma_{\hat{\theta}}} \le \cfrac{k - \theta_a}{\sigma_{\hat{\theta}}} | \theta = \theta_a\right)$
Example 10.8
예제 10.5의 상황에서 가설을 다음과 같이 가정했다고 하자. $H_0: \mu = 15, \quad H_a: \mu = 16$. 10.5와 데이터가 같다고 할 때, $\beta$를 구하시오.
$n=36, \bar{y}=17, s^2=9, \alpha = 0.05$이므로 RR을 구하면 $z = \cfrac{\bar{y} - \mu_0}{\sigma / \sqrt{n}} > 1.645$
이를 전개하면 $\bar{y} > \mu_0 + 1.645\left( \cfrac{\sigma}{\sqrt{n}} \right), \bar{y} > 15.8225$
따라서 $\beta = P(\bar{Y} \le 15.8225) = P\left( \cfrac{\bar{Y} - \mu_a}{\sigma / \sqrt{n}} \le \cfrac{15.8225 - 16}{3 / \sqrt{36}} \right) = P(Z \le -0.36) = 0.3594$
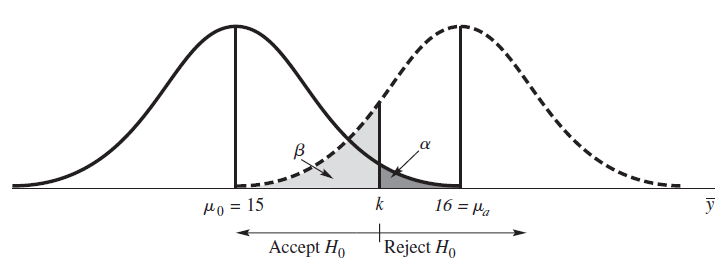
반대로, $\alpha, \beta$가 정해진 경우 sample size $n$을 계산할 수 있다. $\alpha$, $\beta$의 정의를 따라 $z_{\alpha}, z_{\beta}$를 구하고 두 식을 연립하고 $n$을 구한다.
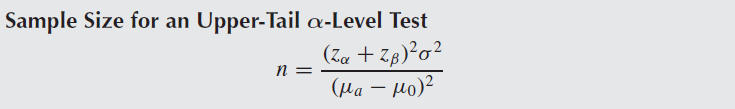
Example 10.8
예제 10.5에서 부사장은 다음과 같이 가설을 검증하려고 한다.
$$H_0: \mu = 15, H_a: \mu = 16$$ with $\alpha = \beta = 0.05$
모분산이 9일때, 이 정확도를 유지하는 표본의 개수(sample size)를 구하시오.
$z_{\alpha} = 1.645, z_{\beta} = 1.645$이므로 $n = \cfrac{(1.645 + 1.645)^{2} (9)}{(16 - 15)^2} = 97.4$
따라서 $n=98$이 $\alpha \approx \beta \approx 0.05$인 표본의 크기가 된다.
10.5 Relationships Between Hypothesis-Testing Procedures and Confidence Intervals
신뢰계수가 $1 - \alpha$일 때 신뢰구간은 $\hat{\theta} \pm z_{\alpha / 2}\sigma_{\hat{\theta}}$ 임을 배웠다.
(이때 $P(Z > z_{\alpha / 2} = \alpha / 2)$를 만족한다)
large-sample에서, $H_0: \theta = \theta_0$, $H_a: \theta \neq \theta_0$, $Z = \cfrac{\hat{\theta} - \theta_0}{\sigma_{\hat{\theta}}}$, RR = {$|z| > z_{\alpha / 2}$} 인 양측검정을 생각하자.
이때 $H_0$가 채택되는(기각되지 않는) 경우는
$$\hat{\theta} - z_{\alpha / 2}\sigma_{\hat{\theta}} \le \theta_0 \le \hat{\theta} + z_{\alpha / 2}\sigma_{\hat{\theta}}$$
이는 $100(1 - \alpha)%$의 신뢰구간 유의수준이 $\alpha$인 양측검정은 동일한 구간을 갖는다.
Exercise 10.21, 10.45
(10.21) 두 종류의 토양의 압축실험에서 얻은 전단강도(shear strength)에 대한 데이터는 아래와 같을 때, 1% 유의수준에서 평균 강도는 다르다고 할 수 있는가?
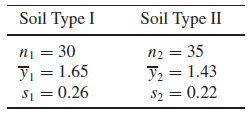
주장하는 가설이 평균이 다르므로, $H_0: \mu_1 - \mu_2 = 0 \quad H_a: \mu_1 - \mu_2 \neq 0$
$Z = \cfrac{(\bar{Y_1} - \bar{Y_2}) - (\mu_1 - \mu_2)}{\sqrt{\cfrac{\sigma_1^2}{n_1} + \cfrac{\sigma_2^2}{n_2} }}$ 에서 large-sample이므로 모분산 대신 표본분산을 사용해도 무방한다.
$z = \cfrac{1.65 - 1.43}{\sqrt{\cfrac{(0.26)^2}{30} + \cfrac{(0.22)^2}{35} }} = 3.648$이고
$z_{\alpha / 2} = z_{0.005} = 2.5758$ 이다
$z$가 기각역에 속하므로 $H_0$를 기각한다. (즉 토양의 전단강도의 평균은 서로 다르다)
(10.45 - a) 두 토양의 전단강도 평균의 차에 대한 99% 신뢰구간을 구성하려고 한다. $\mu_1 - \mu_2$는 이 구간의 안에 있는가, 밖에 있는가?
(10.45 - b) 신뢰구간에 기반하여, 10.21에서 언급된 귀무가설은 기각될 수 있는가?
(10.45 - c) 10.21의 결론과 이번의 결론을 비교하라.
99%의 신뢰구간은 $1.65 - 1.43 \pm 2.576\sqrt{\cfrac{(0.26)^2}{30} + \cfrac{(0.22)^2}{35}} = 0.22 \pm 0.155 (0.065, 0.375)$이다. 이 신뢰구간은 $0$을 포함하지 않으므로 $H_0$은 기각된다. 즉 10.21과 결론이 같다.
10.6 Another Way to Report the Results of a Statistical Test: Attained Significance Levels, or p-Values
획득된 유의수준, p-value, p-값
앞서 보았듯이, 1종오류의 확률 $\alpha$는 유의수준(significance level, level)이라고 불린다. $\alpha$의 값이 적을 수록 좋지만(선호되지만), 그 값을 정하는것은 임의적이다. 누구는 $\alpha = 0.05$라고 하고 누구는 $\alpha = 0.01$이라 할 것이다. 이는 곧 같은 데이터임에도 불구하고 다른 결과(기각 또는 채택)을 야기할 수 있다.
일단 Y나 Z와 같은 검정통계량이 결정되면, p-value 또는 유의확률을 보고하는 것이 일반적이다. 이 값들은 귀무가설이 기각되는 가장 작은 $\alpha$를 나타내는 통계량이다.
p-value는 귀무가설이 기각될 수 있는 가장 작은 $\alpha$의 값이다.
p-value가 작을 수록, 귀무가설을 기각해야한다는 증거가 설득력을 갖는다. p-value가 당신을 설득하기 충분히 작다면, 당신은 귀무가설을 기각해야한다.
p-value는 귀무가설을 기각할 수 있는 $\alpha$의 최솟값이다. 즉, $\alpha$가 p-value보다 크거나 같다면, 귀무가설은 기각되어야한다. 반대로, $\alpha$가 p-value보다 작다면 귀무가설은 기각할 수 없다.
어떤 의미에서, p-value는 데이터가 귀무가설과 일치하는지에 대한 평가로 간주될 수 있다.
p-value를 찾는 과정은 다음 예제처럼 따른다.
Example 10.10
예제 10.1~10.4에서 논의된 정치인 여론조사를 떠올려보자. ($n=15$) $Y$가 Jones에게 투표한 사람들의 수일 때, 가설 $H_0: p=0.5$ 대(versus) $H_a: p < 0.5$ 에 대한 검정을 한다고 하자. 이때 $Y=3$일 때의 p-value는 무엇인가? 그 결과를 해석하라.
$Y$는 $n=15, p=0.5$인 이항분포를 따르고, p-value는 P{Y \le 3}이다. 이항분포표를 이용하면 p-value = 0.018이다.
따라서 $\alpha \ge 0.018$이면 귀무가설 $H_0$를 기각해야 한다.
Excercise 10.56
어떤 제약회사에서 감기가 발병한 후 나타나는 합병증과 회복 평균 시간(단위: 일)을 비교하는 실험을 진행했다. 이 실험은 비타민C를 복용/복용하지 않은 집단 2개로 나눠서 진행하였고, 35명의 성인을 임의로 선택하였다.
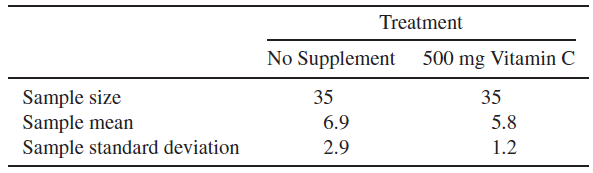
(a) 데이터는 비타민C 복용이 회복시간 단축을 했다고 볼 수 있는가? 획득된 유의수준을 구하여라.
(b) 만약 회사가 $\alpha = 0.05$라 했을 때 어떤 선택을 내릴 것인가?
$H_0: \mu_1 - \mu_2 = 0 \quad H_a: \mu_1 - \mu_2 > 0$
$n_1 = 35, n_2 = 35, \mu_1 = 6.9, \mu_2 = 5.8, \s_1 = 2.9, s_2 = 1.2$ 이므로 $z = \cfrac{6.9 - 5.8}{\sqrt{((2.9)^2 + (1.2)^2) / 35}} = 2.074$
따라서 p-value = $P(Z > 2.074) = 0.0192$이므로 $\alpha$보다 작기 때문에 귀무가설을 기각한다. 따라서 비타민C는 회복시간 감소에 효과가 있다.
10.7 Some Comments on the Theory of Hypothesis Testing
생략
10.8 Small-Sample Hypothesis Testing for $\mu$ and $\mu_1 - \mu_2$
$Y_1, Y_2, ..., Y_n$을 평균과 분산을 알 수 없는 정규분포에서 랜덤 추출한 $n$개의 표본이라 하자. 그리고 $\bar{Y}, S$는 각각 표본평균과 표본표준편자이다. 만일 귀무가설 $H_0: \mu=\mu_0$가 참일 때 확률변수$T$는
$$T = \cfrac{\bar{Y} - \mu_0}{S / \sqrt{n}} ~ t(n-1)$$
이다. (자유도가 $(n-1)$인 t분포를 따른다)
t분포 역시 대칭적이기 때문에 Z-test처럼 기각역을 RR = {$t > t_{\alpha}$} 이다.


Example 10.14, 10.15
데이터가 아래와 같을 때, $\alpha = 0.05$에서 검정을 하시오. 그리고 p-value를 구하시오.
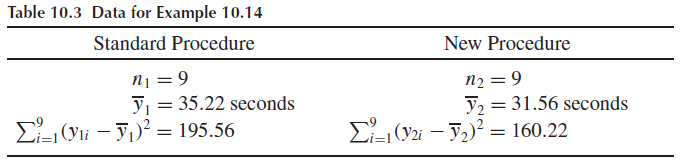
$H_0: (\mu_1 - \mu_2) = 0, \quad H_a: (\mu_1 - \mu_2) \neq 0$ 라 하면 양측검정이 필요하다. 즉 기각역은 {$|t| > t_{\alpha / 2} = t_{0.025} = 2.120$} 이다. (자유도가 $9+9-2 = 16$임에 유의한다)
합동표본분산을 구하면 $s_p = \sqrt{s_p^2} = \sqrt{\cfrac{195.56 + 160.22}{9+9-2}} = \sqrt{22.24} = 4.716$
따라서 $t = \cfrac{35.22 - 31.56}{4.176\sqrt{1/9 + 1/9}} = 1.65$
$t$는 기각역 RR에 포함되지 않으므로 귀무가설은 기각되지 않는다.
또한 p-value는 $P(T > 1.65) + P(T < -1.65) = 2(0.0592) = 0.1184$ 이므로(자유도는 16이다.) $\alpha$보다 크다. 따라서 이 경우에도 귀무가설을 기각할 수 없다.
Exercise 10.77
연습문제 8.90에서봤던, 공학계열과 어문계열 진학을 희망하는 학생들의 SAT 점수 데이터이다.

(a) verbal 점수에서 공학계열과 어문계열 진학 집단의 평균의 차이가 있다는 충분한 근거가 있는가? 유의수준 $\alpha = 0.05$일 때의 p-value의값(또는 영역)을 구하고, 결론을 내려라.
(a - solution)$H_0: \mu_1 - \mu_2 = 0, \ \textrm{vs} \ H_a: \mu_1 - \mu_2 \neq 0$이다. ($\mu_1, \mu_2$는 각각 공학/어문계열의 verbal 점수의 평균이다). 양측검정 이용
$s_p^2 = \cfrac{14(42)^2 + 14(45)^2}{28} = 1894.5$이므로 $s_p = 43.526$.
$t = \cfrac{446 - 534}{(1894.5)(\cfrac{2}{15})} = -5.54$이고, 자유도는 $28$일 때 검정통계량 $t$는 $0 < P(t \le -5.54) < 0.005$ 이고 양측검정에 따라 p-value = $2 \times P(t \le -5.54)$이고 이는 $0.01$보다 작다. 따라서 귀무가설을 기각한다.
(b) 연습문제 8.90(신뢰구간 구하기)와 (a)의 결론이 같은가?
(b - solution) 신뢰구간 CI는 $\bar{y_1} - \bar{y_2} \pm t_{(\alpha/2, \ n_1 + n_2 - 2)} \cdot s_p\sqrt{\cfrac{1}{n_1} + \cfrac{1}{n_2}}$로 구한다. $t_{(\alpha,\ n_1 + n_2 - 2)} = t_{0.001, 28} = 2.467$므로 신뢰구간은 $(-120.56,\ -55.44)$이고, $0$은 신뢰구간에 존재하지 않는다. 따라서 귀무가설을 기각한다. (a)와 결론이 같다.
(c, d) Math에서도 (a)와 동일한 검정을 하여라.
$s_p^2 = \cfrac{14(57)^2 + 14(52)^2}{28} = 2976.5$, $t = \cfrac{548 - 517}{(2976.5)\cfrac{2}{15}}=1.56, \ df = 28$
따라서 p-value는 0.1보다 크고 0.2보다 작다. 귀무가설을 기각할 수 없다. (귀무가설을 채택한다)
10.9 Testing Hypothesis Concerning Variances
모분산 검정

Example 10.16, 10.17
어떤 외사는 기계 엔진 부품을 생산하는데, 지름의 분산은 0.0002(인치) 보다 크지 않아야 한다고 한다. 10개의 랜덤샘플의 표본분산은 0.0003이라고 한다. \
(10.16) 5% 유의수준에서, 가설을 검정하라. $H_0:\ \sigma^2 = 0.0002 \ H_a:\ \sigma^2 > 0.0002$
(10.17) p-value를 구하여라.
지름의 분포를 정규분포를 따른다고 가정한다면, 통계량은 $\chi^2 = \cfrac{(n-1)s^2}{\sigma_0^2} = \cfrac{(9)(0.0003)}{0.0002} = 13.5$ 이고, $\chi^2_{0.05} = 16.919 \ (df=9)$ 이므로 기각역에 포함되지 않는다. 따라서 귀무가설을 기각하지 않는다. (귀무가설을 채택한다). 모분산 $\sigma^2$이 5%의 유의수준에서 0.0002를 넘는다는 증거가 충분치 않다.
$\chi^2_{0.1}=14.6837 (df=9)$임을 표를 통해 알 수 있다. 즉 p-value는 0.1보다 크다. 따라서 귀무가설을 기각할 수 없다.
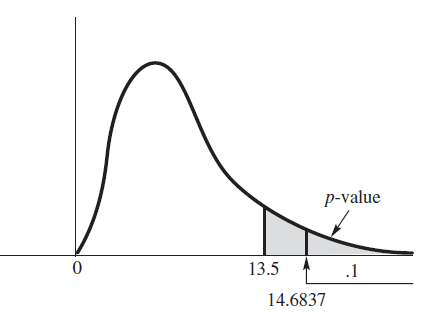
Example 10.18
어떤 학자는 그의 실험 관측의 표준편차가 $2$라고 확신을 가졌다. 16개의 표본에서 표본분산은 $s^2 = 6.1$이라고 한다. 데이터는 학자의 주장을 반대하는가? $\alpha = 0.05$일 때 p-value를 구하여 가설을 검정하여라.
$H_0: \sigma^2 = 4. \ H_a: \sigma^2 \neq 4$ -> 양측검정
분산검정이므로 검정통계량은 카이제곱인 $\chi^2 = \cfrac{(16 - 1)(6.1)}{4} = 22.875$
카이제곱분포표를 이용하면 $\chi^2_{0.05} = 24.9958, \ \chi^2_{0.10} = 22.3072$이므로 이 값은 0.05와 0.1 사이의 값을 갖는다. 즉 $0.1 < 2 \times \textrm{p-value} < 0.2$ 이므로 귀무가설을 기각할 수 없다. (실제로 $P(\chi^2 > 22.875) = 0.0868$이므로 p-value = $2(0.0868) = 0.1736$이다.)
다음은, 2개의 정규분포에서 추출된 경우에서 분산을 검정해보자.
$Y_{11}, Y_{12}, .., Y_{1n_1}$, $Y_{21}, Y_{22}, .., Y_{2n_2}$은 평균과 분산을 모르는 두개의 정규분포에서 추출된 랜덤샘플이라 하자. 그리고 분산은 $V(Y_{1I}) = \sigma_1^2, \ V(Y_{2i}) = \sigma_2^2$이다.
우리의 가설은 $H_0: \sigma_1^2 = \sigma_2^2. \quad H_a: \sigma_1^2 > \sigma_2^2$
표본분산 $S_1^2,\ S_2^2$이 모분산의 추정량이기 때문에, 기각역은 RR = $\{ \cfrac{S_1^2}{S_2^2} > k \}$이고 $k$는 1종오류의 확률인 $\alpha$로 결정되는 수이다.
확률변수 F는 $F = \cfrac{(n_1 - 1)S_1^2}{\sigma_1^2(n_1 - 1)} / \cfrac{(n_2 - 1)S_2^2}{\sigma_2^2(n_2 - 1)} = \cfrac{S_1^2 \sigma_2^2}{S_2^2 \sigma_1^2}$가 되고 자유도는 $(n_1 - 1, n_2 - 1)$로 표기하고 각각 분자, 분모의 자유도를 나타낸다.
귀무가설 $H_0: \sigma_1^2 = \sigma_2^2$에서 $F = S_1^2/S_2^2$이고 기각역 RR = {F > F_{\alpha}}이다. (자유도는 $(n_1 - 1, n_2 - 1)$)
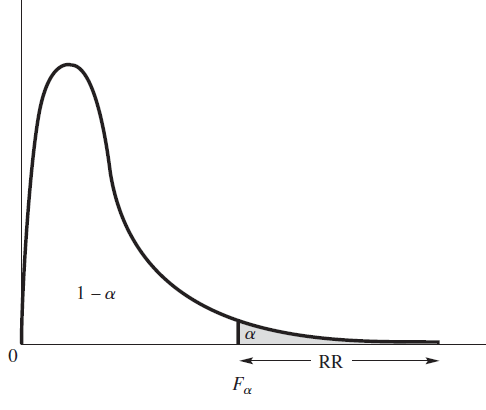
Example 10.19, 10.20
예제 10.16에서 살펴본 어떤 회사에서 생산한 부품의 지름에 대한 분산을 비교하려한다. $n=10$일때 $s_1^2 = 0.0003$이고, $n=20$일 때 $s_2^2 = 0.0001$이었다. 1번은 자사, 2번은 경쟁사이다.
(10.19) $\alpha = 0.05$일 때, 경쟁사는 더 적은 분산을 갖는다고 충분한 근거가 있는가?
가설을 세우면 $H_0: \sigma_1^2 = \sigma_2^2. \quad H_a: \sigma_1^2 > \sigma_2^2$
검정통계량은 $F = 0.0003/0.0001 = 3$이고 자유도는 (9, 19)이다.
$F_{\alpha} = F_{0.05} = 2.42$이고 $F > F_{0.05}$이므로 귀무가설을 기각한다. 따라서 경쟁사의 분산이 더 작다고 말할 수 있다.
(10.20) p-value를 구하여라
자유도가 (9, 19)인 F분포표를 보면 $F_{0.025} = 2.88,\ F_{0.01} = 3.52$이므로 $\alpha = 0.025$일 때는 귀무가설을 기각할 수 있지만 $\alpha = 0.01$일 때에는 귀무가설을 기각할 수 없다. 그러므로 0.01 < p-value < 0.025 이다. 실제 p-value는 0.02096이다.

만일 $H_0: \sigma_1^2 = \sigma_2^2. \quad H_a: \sigma_1^2 < \sigma_2^2$을 검정하고 싶다면, 쉽게 1과 2를 바꾸면 된다. 이 때, 자유도의 순서가 바뀜에 조심한다. 그리고 F분포의 특징을 이용해도 좋다. ($F = S_1^2/S_2^2$ 일 때 $F^{-1} = S_2^2/S_1^2$)
만일 $H_0: \sigma_1^2 = \sigma_2^2. \quad H_a: \sigma_1^2 \neq \sigma_2^2$을 검정하고 싶다면, $F = S_1^2/S_2^2$에 대한 양측검정을 하면 된다. 이때의 기각역은 RR = {$F > F^{(n_1 - 1, n_2 - 1)}_{\alpha / 2} \ \textrm{or} \ F < (F^{(n_2 - 1, n_1 - 1)}_{\alpha / 2})^{-1}$}
Example 10.21
다음은 남녀에 대한 전기자극에 대한 고통의 역치 데이터이다. $\alpha = 0.1$일 때 남성과 여성의 분산이 다르다고 할 수 있는가? p-value(의 값 또는 범위)는 무엇인가?
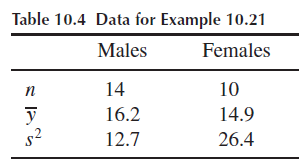
$H_0: \sigma_M^2 = \sigma_F^2. \quad H_a: \sigma_M^2 \neq \sigma_F^2$
표본분산은 여성이 더 크므로 1은 여성, 2는 남성의 데이터로 표기한다.
검정통계량은 $F = \cfrac{26.4}{12.7} = 2.079$이고 자유도는 (9, 13)이다.
양측검정이므로 $F^{(9, 13)}_{\alpha / 2} = F_{0.05} = 2.71$
F가 기각역에 존재하지 않기 때문에 남녀 분산의 차이가 있다고 충분한 근거가 되지 않는다.
자유도가 (9, 13)인 F분포표에서 $F_{0.1} = 2.16$임을 알 수 있다. 따라서 p-value > 2(0.1) = 0.2이다. p-value가 $\alpha$보다 크기 때문에 귀무가설을 기각할 수 없다.
카이제곱검정과 F검정 모두 정규분포라는 가정하에 예민하게 이루어진다. 즉, t검정과 달리, 정규분포라는 가정이 없다면 카이제곱검정과 F검정은 not robust하다.
10.10 Power of Tests and the Neyman-Pearson Lemma
이번 장에서는 좀 더 이론적인 가설검정으로 들어간다. 앞에서 몇가지 가설검정의 방법을 배웠지만 왜 이렇게 해야하는지를 배울 차례이다.
좋은 검정은 $\alpha, \beta$로 결정된다. 일반적으로, $\alpha$는 미리 값이 정해지고 기각역의 위치를 결정한다. 이와 관련된 유용한 개념으로 검정의 지표는 검정력(power of the test)라고 한다. 기본적으로, 검정력은 귀무가설을 기각할 확률이다.
$$\textrm{power}(\theta) = P(W \textrm{in RR when the parameter value is }\theta)$$
$H_0: \theta = \theta_0$이고, $\theta_a$는 $H_a$에서 고른 어떤 값이라고 하자. 이때 $\textrm{power}(\theta_a) = P(\textrm{rejecting }H_0 \textrm{when } \theta=\theta_a)$이다. 즉 1종오류를 범할 확률이다.
반대로, 2종오류를 범할 확률을 구하면 $\beta(\theta_a) = P(\textrm{accepting }H_0 \textrm{when } \theta=\theta_a)$
여기서 검정력(Power)와 $\beta$와의 관계를 알 수 있다.
$$\textrm{power} (\theta_a) = 1 - \beta(\theta_a) \ \textrm{when }\ \theta_a \textrm{ is a value of} \ \theta \textrm{ in the } \ H_a$$
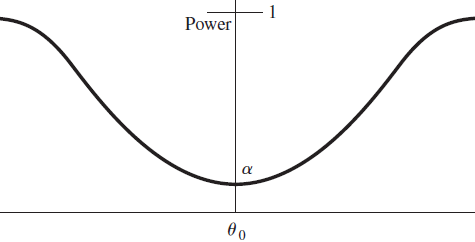
이상적인 경웨, 가설은 $H_0: \theta = \theta_0$로부터 떨어짐을 탐지할 것이다. 즉 power($\theta_a$) = 1 이 될 것이다.
고정된 표본크기일 때 $\alpha, \beta$ 모두 작게 만들 수 없기 때문에, 우리는 작은 $\alpha$를 선택하고, $\beta(\theta_a)$를 최소화하는 기각역 RR을 찾는 절차를 선택한다. 마찬가지로, 우리는 $H_a$에 있는 $\theta$에 대해 $power($\theta$)를 최대화 하는 RR을 선택한다. 유의수준이 $\alpha$인 모든 가설중에서, 우리는 이상적인 검정력함수(power function)에 가장 가까운 검정력함수를 찾을 것이다. 그런데 어떻게 그러한 절차를 찾을 수 있을까?
논의를 진행하기 전에, 우리는 단순가설(simple hypothesis)과 복합가설(composite hypothesis)를 정의해야한다.
$Y_1, ..., Y_n$이 모수가 $\lambda$인 지수분포에서 추출된 랜덤샘플이라고 하자.($f(y) = (1/\lambda)e^{-y/\lambda}$)
그리고 가설 $H: \lambda = 2$는 오로지 한개의 분포 $f(y) = (1/2)e^{-y/2}$를 특정한다. 이때 가설 $H$를 단순가설이라고한다.
반대로, 가설 $H*: \lambda > 2$는 $f(y)$를 하나로 결정할 수 없기 때문에 복합가설이라고 한다. ($\lambda$는 2보다 큰, 예를 들어 3, 15 모두 가능하기 때문)
모수가 $\theta$인 분포에서 랜덤샘플을 추출했을 때,
어떤 가설이 확률분포를 하나로 결정하면 단순가설(simple hypothesis)이라고 하고,
그렇지 않은 경우(단순가설이 아니면) 복합가설(composite hypothesis)라고 한다.
예를 들어, $Y_1, ..., Y_n$가 분산이 $\sigma^2 = 1$이 알려져 있는 정규분포에서 추출된 랜덤샘플이라고 하자.
이때 $H: \mu = 5$는 단순가설이다. 왜냐하면 $H$가 참이면 평균과 분산이 각각 5, 1로 고정된 정규분포가 되기 때문이다.
만약에 분산이 알려져있지 않다면, 이때의 가설 $H: \mu = 5$는 복합가설이다. 왜냐하면 분산이 정해져 있기 때문에 하나의 분포로 확정지을 수 없기 때문이다.
두개의 단순가설을 검정한다고 하자. $H_0: \theta=\theta_0 \ \textrm{vs} \ H_a: \theta = \theta_a$
두개의 $\theta$ (\theta_0, \theta_a)에 대해 고려하기 때문에 우리는 기각역 RR은 $\alpha = \textrm{power}(\theta_0)$는 고정값이고 $\textrm{power}(\theta_a)$는 최대로 하는 기각역 RR을 구할 것이다. 다시말해서, 우리는 유의수준이 $\alpha$인 최강력검정(most powerful $\alpha$ level test)를 찾을 것이다. 뒤에 나오는 네이만-피어슨 정리는 두 단순가설데 대해 최강력검정법을 하는 방법이다.
네이만-피어슨 정리(The Neyman-Pearson Lemma)
모수가 $\theta$인 확률분포에서 추출된 $Y_1, ..., Y_n$에 대하여, 단순 귀무가설($H_0: \theta = \theta_0$)과 단순 대립가설($H_a: \theta = \theta_a$)을 검정하려고 한다. $L(\theta)$가 가능도 함수이고, $\alpha$가 주어졌을 때, $\theta_a$에서 검정력을 최대로 하는 검정은 $\cfrac{L(\theta_0)}{L(\theta_a)} < k$ 에 의해 결정되는 기각역 RR을 갖는다. 이와 같은 검정을 유의수준이 $\alpha$인 $H_0$ 대 $H_a$의 최대검정법이라 한다.
Example 10.22
$f(y | \theta) = \theta y^{\theta - 1},\ (0 < y < 1)$에서 유의수준이 $\alpha=0.05$이고 $H_0: \theta = 2 \ \textrm{vs} \ H_a: \theta=1$에 대한 최강력검정을 구하여라.
$\cfrac{L(\theta_0)}{L(\theta_a)} = \cfrac{f(y|\theta_0}{f(y|\theta_a)} = \cfrac{2y}{(1)(y^0} = 2y, (0 < y < 1)$이므로 $2y < k$, 즉 RR = {$y < k/2$} = {$y < k^*$}
$\alpha=0.05$로 특정되므로 $k$*$를 구하면
$$0.05 = P(Y \textrm{ in RR when}\ \theta=2) = \displaystyle\int_{0}^{k^*}2ydy = (k^*)^2$$
$k^* = \sqrt{0.05}$, 따라서 RR = {$y < \sqrt{0.05} = 0.2236$}
Example 10.23
$Y_1, ..., Y_n$이 평균과 분산이 각각 $\mu, \sigma^2$인 정규분포에서 추출한 랜덤샘플이라 하자. 우리는 가설 $H_0: \mu = \mu_0 \ \textrm{against} \ H_a: \mu > \mu_0$를 검정하려고 한다. (분산은 알려져 있고, 평균은 안알려져있다) 유의수준이 $\alpha$일 때의 최강력검정을 구하시오.
가설을 $H_0: \mu=\mu_0 \ \textrm{vs} \ H_a: \mu=\mu^*\ (\mu^* > \mu)$ 로 세팅하고
$$f(y|\mu) = \left( \cfrac{1}{\sigma \sqrt{2\pi}} \right) \textrm{exp}\left[ \cfrac{-(y - \mu)^2}{2\sigma^2} \right]$$ 이므로
$$L(\mu) = \left( \cfrac{1}{\sigma \sqrt{2\pi}} \right)^{n} \textrm{exp}\left[-\displaystyle\sum_{i=1}^{n} \cfrac{(y - \mu)^2}{2\sigma^2} \right]$$
따라서 $\cfrac{L(\mu_0)}{L(\mu_a)} < k$를 계산하면
$$\textrm{exp} \left\{ -\cfrac{1}{2\sigma^2}\left[ \sum_{i=1}^{n}(y_i - \mu_0)^2 - \sum_{i=1}^{n}(y_i - \mu_a)^2 \right] \right\} < k$$
양변에 자연로그를 취하면
$$\displaystyle\sum_{i=1}^{n}(y_i - \mu_0)^2 - \sum_{i=1}^{n}(y_i - \mu_a)^2 > -2\sigma^2 \ln{(k)}$$
$$\sum_{i=1}^{n}y_i^2 -2n\bar{y}\mu_0 + n\mu_0^2 - \sum_{i=1}^{n}y_i^2 + 2n\bar{y}\mu_a - n\mu_a^2 > -2\sigma^2\ln{(k)}$$
$$\bar{y} > \cfrac{-2\sigma^2\ln{(k)} -n\mu_0^2 +n\mu_a^2 }{2n(\mu_a-\mu_0)} = k^{'}$$
따라서 RR = { $\bar{y} > k^{'}$ }
$k^{'}$의 값을 구하기 위해 $\alpha$를 고정하면
$\alpha = P(\bar{Y} \textrm{ in RR when }\mu = \mu_0) = P(\bar{Y} > k^{'} \textrm{ when }\mu=\mu_0) = P\left( \cfrac{\bar{Y} - \mu_0}{\sigma / \sqrt{n}} > \cfrac{k^{'} - \mu_0}{\sigma / \sqrt{n}} \right) = P(Z > \sqrt{n}(k^{'}-\mu_0)/ \sigma)$
$\sqrt{n}(k^{'}-\mu_0)/ \sigma = z_{\alpha}$라고 하면 $k^{'} = \mu_0 + z_{\alpha}\sigma / \sqrt{n}$
식을 살펴보면, $\mu_a$의 값과는 상관없다는 것을 알 수 있다. 따라서 $\mu_a > \mu_0$이기만 한다면, 항상 동일한 기각역 RR을 얻게 된다는 뜻이다. 이는 균일최강력검정법(the uniformly most powerful test)이라고 부른다.
10.11 Likelihood Ratio Tests
10.12 Summary
'스터디 > 확률과 통계' 카테고리의 다른 글
| [확률] 생일문제 (0) | 2023.03.02 |
|---|---|
| [확률] 베이즈 정리 (Bayes' theorem) (0) | 2023.02.18 |
| Chapter 9. Properties of Point Estimators and Methods of Estimation (0) | 2022.08.13 |
| Chapter 8. Estimation (0) | 2022.08.05 |
| Chapter 4. Continuous Variables and Their Probability Distributions (0) | 2022.07.30 |



