1. Introduction
ICLR 2023에 publish된 논문이고 주된 내용은
- interperiod-variation, intraperiod-variation(기간내, 기간 간 변동) 모두 포착하는 모델 아키텍처 제안
- 1차원 시계열 데이터를 2차원 데이터로 변환하여 convolution으로 feature extraction
- ResNet의 residual block을 이용한 TimesBlock 제안
- 파라미터 수를 줄이기 위해 GoogLeNet의 Inception 사용
- 5개의 General Task에 대하여 SOTA 달성
- 장기 예측(long-term forecasting)
- 단기 예측(short-term forecasting)
- 결측치 대입(imputation)
- 분류(classification)
- 이상치 탐지(anomaly detection)
2. Related Work
과거 시계열 모델은 크게 3가지 방법론이 제안되었다.
- Clasical Methods
- ARIMA
- Holt-Winter
- Prophet
- Deep Model
- RNN-based
- MLP-based
- TCN-based
- Transformers: Attention mechanism은 시간적 의존성(temporal dependency)를 잘 포착한다.
- Autoformer
- FEDformer
3. TimesNet
각 시계열 데이터에는 period가 다르고, 각 period는 temporal pattern을 갖는다.
각 period마다 interperiod, intraperiod-variation이 존재한다.
따라서 1차원 데이터를 2차원으로 펼쳐서(?) 패턴을 찾는다.
3.1 Transform 1D-variations into 2D-variations

$T$: length of time series
$C$: the number of recorded variates
$\mathbf{X}_{\text{1D}} \in \mathbb{R}^{T \times C}$
interperiod-variation (FFT analysis)

- $\mathbf{A} = \text{Avg}\left( \text{Amp}(\text{FFT}(\mathbf{X}_{\text{1D}})) \right)$
- $\mathbf{A}$: amplitude of each frequency
- $\mathbf{A} \in \mathbb{R}^T$
- $\{ f_1, \cdots, f_k\} = \underset{f_* \in \set{1, \cdots , [\frac{T}{2}]}}{\text{argTopK}(\mathbf{A})}$
- use top-k frequencies to avoid meaningless high frequencies
- $k$ is hyperparameter; $k=2$ is default in GitHub
- $p_i = \lceil\cfrac{T}{f_i} \rceil, i \in \set{ 1, \cdots, k}$
- Selected frequencies correspond to $k$ period lengths $\set{p_1, \cdots, p_k}$
최종적으로 FFT를 이용하여 얻는 결과는 3개(진폭 $\mathbf{A}$ 집합, 주파수 $f$ 집합, 주기 $p$ 집합)이며, 이를 한줄로 표현하면 다음과 같다.
\[ \mathbf{A}, \{f_1, \cdots, f_k\}, \{p_1, \cdots, p_k\} = \text{Period}(\mathbf{X}_{\text{1D}}) \]
Reshape 1D time sereis into multiple 2D tensors
$$ \mathbf{X}_{\text{2D}}^i = \underset{p_i, f_i}{\text{Reshape}}(\text{Padding}(\mathbf{X}_{\text{1D}})), \quad i \in \set{1, \cdots, k}$$
Padding: Reshape를 하기 위해 zero-padding 적용
$p_i, f_i$는 2D-tensor의 row, column
row는 interperiod-variation을, column은 intraperiod-variation time point끼리 인접한다.
$k$개의 period에 대해 2D-tensor로 reshape하므로 $\set{\mathbf{X}_{\text{2D}}^1, \cdots, \mathbf{X}_{\text{2D}}^k}$를 얻는다.

3. TimesBlock
vision deep learning model 아키텍처에서 사용된 아이디어(residual network, inception 등)를 차용했다.
TimesBlock
- $\mathbf{X}_{\text{1D}}^0 = \text{Embed}(\mathbf{X}_{\text{1D}})$
- $\mathbf{X}_{\text{1D}} \in \mathbb{R}^{T \times C}$를 $\mathbf{X}_{\text{1D}}^0 \in \mathbb{R}^{T \times d_{model}}$로 projection
- embedding layer를 이용하여 projection
- $l$-layer는 아래의 연산을 반복하여 $\mathbf{X}_{\text{1D}}^l \in \mathbb{R}^{T \times d_{model}}$예산
- $\mathbf{X}_{\text{1D}}^l = \text{TimesBlock}(\mathbf{X}_{\text{1D}}^{l-1}) + \mathbf{X}_{\text{1D}}^{l-1}$
- $\text{TimesBlock}$은 2D-variation을 포착하면서 different period의 표현을 aggregate한다.
Capturing temporal 2D-variations
1. $\mathbf{A}^{l-1}, \{f_1, \cdots, f_k\}, \{p_1, \cdots, p_k\} = \text{Period}(\mathbf{X}_{\text{1D}}^{l-1})$
2. $\mathbf{X}_{\text{2D}}^{l, i} = \underset{p_i, f_i}{\text{Reshape}}(\text{Padding}(\mathbf{X}_{\text{1D}}^{l-1})) \quad i \in \set{1, \cdots, k}$
3. $\widehat{\mathbf{{X}}}_{\text{2D}}^{l, i} = \text{Inception}(\mathbf{X}_{\text{2D}}^{l, i}), \quad i \in \set{1, \cdots, k}$
4. $\widehat{\mathbf{{X}}}_{\text{1D}}^{l, i} = \text{Trunc}(\underset{1, (p_i \times f_i)}{\text{Reshape}}(\widehat{\mathbf{{X}}}_{\text{2D}}^{l, i})), \quad i \in \set{1, \cdots, k}$
5. 최종적으로 $k$개의 1D-representation $\set{\widehat{\mathbf{X}}_{\text{1D}}^{l, 1}, \cdots, \widehat{\mathbf{X}}_{\text{1D}}^{l, k}}$을 얻는다.

Adaptive aggregation
Auto-Correlation의 아이디어: amplitude $\mathbf{A}$는 relative importance를 반영한다.
$$\widehat{\mathbf{A}}_{f_1}^{l-1}, \cdots, \widehat{\mathbf{A}}_{f_k}^{l-1} = \text{Softmax}\left(\mathbf{A}_{f_1}^{l-1}, \cdots, \mathbf{A}_{f_k}^{l-1} \right)$$
$$\mathbf{X}_{\text{1D}}^l = \sum_{i=1}^{k} \widehat{\mathbf{A}}_{f_i}^{l-1} \times \widehat{\mathbf{X}}_{\text{1D}}^{l, i}$$
Generality in 2D vision backbones
저자들은 (2D kernel을 이용하므로) vision task의 아키텍처들을 다양한 백본으로 삼는 것을 추천했다.
- Inception block
- ResNet
- ResNeXt
- ConvNeXt
- attention-based mode
More powerful 2D backbones will bring better performance
성능이나 효율성(파라미터 수 등)을 고려했을 때, Inception 을 이용한 backbone이 가장 좋다고 한다.
4. Experiments
다양한 time series dataset과 다양한 모델들과 성능을 비교하였다.
그리고 각 task별로 당시 SOTA 모델 역시 비교 대상이다.
- RNN-based: LSTM, LSTNet, LSSL
- CNN-based: TCN
- MLP-based: LightTS, DLinear
- Transformer-based: Reformer, Informer, ETSformer
- SOTA for each tasks
- short-term forecasting: N-HiTS, N-BEATS
- anomaly detection: AnomalyTransformer
- Classification: Rocket, Flowformer
자세한 실험결과는 포스팅에서 생략한다. 5개 영역(장기 예측, 단기 예측, 결측치 보강, 분류, 이상치탐지) 모두 SOTA를 달성했다고 한다.

Representation analysis
성능은 검증되었고, 이제 TimesNet이 정말로 제대로 학습을 한 것인지 알아보자. (representation learning 관점에서)
CKA similarity를 살펴보면, 예측, 이상치 탐지는 높은 CKA similarity일 수록 높은 성능을 가졌고, 결측치 보강, 분류 task에세는 반대의 경향을 보인다.
낮은 CKA similarity는 각 layer마다 구별되는 representationn을 갖는다는 뜻이고 곧 hierarchial representation을 갖는다고 볼 수 있다.

위 figure를 살펴보면, TimesNet은 다른 task마다 적절히 represent하는 것을 알 수 있다.
forecasting, anomaly detection에서는 low-level representation
imputation, classification에서는 hierarchical representation
반면에, FEDformer는 평가지표에서 성능은 우수하지만, hierarchical representation learning에는 실패했다. 이때문에 FEDformer는 imputation과 classification에서 성능이 저조한 것이다.
Representation learning이 적절하게 학습되어 task-generality가 검증되었기에, 저자들은 TimesNet이 foundation model이라고 주장한다.
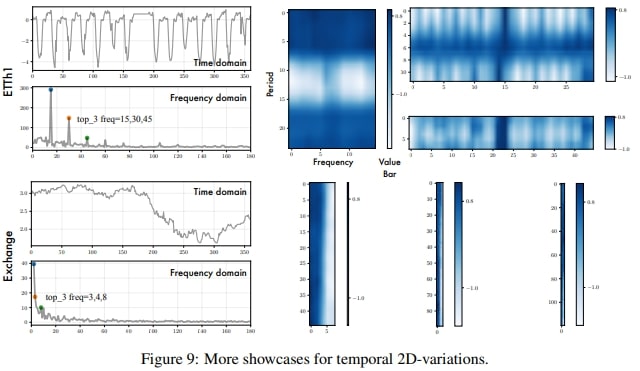
Temporal 2D-variations
Figure 7을 살펴보면, TimesNet은 multi-periodicity를 정확하게 포착하는 것을 알 수 있다. 게다가 2D-tensor는 column과 row가 locality를 잘 반영하고 있음을 알 수 있다.

Appendix-D에 더 자세히 설명되어있다.
interperiod-variation은 long-term trends를 표현할 수 있다.
심지어 명확한 periodicity가 없는 경우에도 2D-tensor는 여전히 informative하다. (FFT analysis로 얻은) frequency가 하나밖에 없다면, intraperiod-variation은 그 자체로 raw series가 된다.
2D-tensor는 2가지 종류의 locality를 보여준다. column은 intraperiod-variation을 표현하는 time point끼리 거리가 가깝고, row의 경우 interperiod-variation을 표현하는 time point끼리 거리가 가깝다.
반면에 인접하지 않는 time point끼리는 서로 꽤 다르고 이는 gloval trend에 의한 영향으로 볼 수 있다. Exchange 데이터셋을 보면 잘 알 수 있다.
5. Conclusion and Future Work
저자들이 제안한 TimesNet은 시계열 분석에 특화된 task-general foundation model임을 보였다. multi-periodicy를 포착하기 위해 TimesNet은 2D-공간에서 intraperiod, interperiod-variation을 표현한다.
실험적으로, TimesNet은 다양한 데이터셋에서 5개의 task에 대하여 SOTA를 달성하였다.
후속 연구로, 저자들은 large-scale pre-training method를 연구하여 TimesNet을 backbone으로 하고 downstream task로 확장하기 위한 연구를 할 것이라 한다.
'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| GAT, GraphSAGE (0) | 2023.04.19 |
|---|---|
| [GCN] Graph Convolutional Network (0) | 2023.04.18 |
| [CS224w] Colab 2 - PyG, OGB, GNN (0) | 2023.03.21 |
| [CS224w] 5. A General Perspective on GNNs (1), 이론편 (0) | 2023.03.11 |
| [CS224w] 5. A General Perspective on GNNs (2), 아키텍처 (0) | 2023.03.10 |



