앞서 Node Embedding을 할 때는 임베딩 벡터를 이용하여 문제를 해결했다.
이제 딥러닝 방법으로 node/edge/graph를 encoding하는 방법으로 나아가자.
그래프 데이터이므로 Grapn Neural Networks(GNN, GNNs)라 부른다.
기존 MLP가 적합하지 않은 이유
Naive하게 인접행렬$\mathbf{A}$을 concat하여 MLP에 적용해보자.
MLP의 결과는 임베딩된 벡터 $\mathbf{z}_{\mathcal{G}}$가 output으로 나온다고 하면
\[ \mathbf{z}_{\mathcal{G}} = \mathrm{MLP}(\mathbf{A}[1] \oplus \mathbf{A}[2] \oplus \dots \oplus \mathbf{A}|\mathcal{V}| ]) \]
그런데, 굳이 계산해보지 않아도 예상되는 문제점이 있다. 그래프는 위상적으로 동일한데 노드의 이름 순서에 따라 입력이 달라지는 문제가 발생한다.

Permutation Invariance & Equivariance
permutation invariance: 인접행렬의 row/column의 순서가 바뀌어도 $f$의 순서가 바뀌지 않는다.
permutation equivariance: 인접행렬의 순서가 바뀌는 대로 $f$의 결과도 같은 순서로 바뀐다.
수학적으로 인접행렬 $\mathbf{A}$, 순열행렬 $mathbf{P}$, 임의의 함수 $f$에 대하여 아래 식을 만족해야 한다.
\[ f(\mathbf{PAP}^\top) = f(\mathbf{A}) \quad \text{(Permutation Invariance)} \]
\[ f(\mathbf{PAP}^\top) = \mathbf{P}f(\mathbf{A}) \quad \text{(Permutation Equivariance)} \]
따라서 같은 그래프 $G = (\mathbf{A}, \mathbf{X})$ 에 대해서 permutation invariance하고 permutation equivariance한 함수 $f$가 필요하다.
Graph Neural Networks consist of multiple permutation invariant/equivariant functions.
이런 이유로, 기존 신경망인 MLP는 사용할 수 없다.
Graph Convolutional Networks
Idea: 이웃 노드들이 그래프의 구조를 결정한다. -> 어떻게 node feature를 전파시킬 것인가?
Aggregate Neighbors
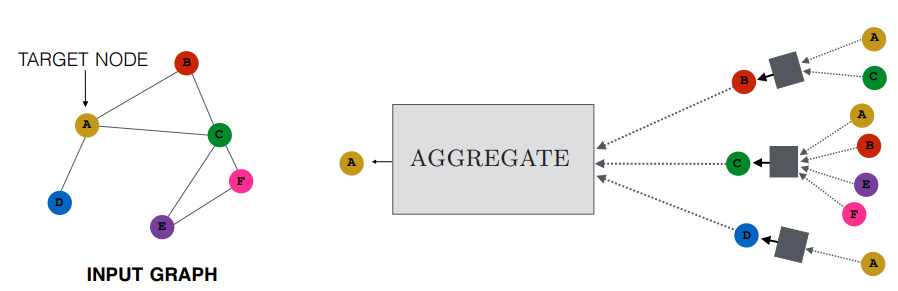
Figure 2의 회색 박스는 일종의 neural networks라고 할 수 있다. 그리고 그 depth는 정하기 나름이다.
$\mathbf{h}_{u}^{(k)}$를 노드 $u$의 $k$번째 hidden embedding이라 하자. 이때 $u$는 그의 이웃노드들 $\mathcal{N}(u)$로부터 정보(아직 정의하지 않음)들을 반복적으로 업데이트하여 $k=K$까지 반복한다.
(AGGREGATE가 $\mathbf{m}$ (Messaging)이 되는 과정은 나중에 설명한다.)
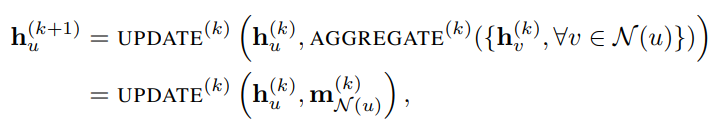
이렇게 학습된 임베딩 노드의 최종 노드는
\[ \mathbf{z}_{u} = \mathbf{h}_{u}^{(K)}, \forall{u} \in \mathcal{V} \]
다시 hidden embedding으로 돌아와서, GNN을 자세히 풀어 써보자.
\[ \mathbf{h}_{u}^{(k)}=\sigma \left( \mathbf{W}_{\text{self}}^{(k)}\mathbf{h}_{u}^{(k-1)} + \mathbf{W}_{\text{neigh}}^{(k)} \sum_{v \in \mathcal{N}(u)}\mathbf{h}_{v}^{(k-1)} + \mathbf{b}^{(k)} \right) \]
이때
$\mathbf{W}$는 $\mathbb{R}^{d^{(k)} \times d^{(k-1)}}$ 인 trainable parameter matrix
$\sigma$: 비선형함수, $\mathrm{tanh}$, $\mathrm{ReLU}$ 등
$\mathbf{b}$: $\mathbb{R}^{d^{(k)}}$: bias
Neighborhood Normalization
neighbor embeddings를 다 더하게 되면 node degree가 높은 노드는 매우 불안정하게 학습될 것이다. 따라서 정규화가 필요하다. 가장 단순한 방법은 이웃하는 노드 수 만큼 나눠주는 것이다.

Kipf and Welling에 따르면 symmetric normalization이 더 좋다고 한다. 그러므로 메시지 $\mathbf{m}$의 형태는 아래와 같다.
\[ \mathbf{m}_{\mathcal{N}(u)} = \sum_{v \in \mathcal{N}(u)} \cfrac{\mathbf{h}_{v}}{|\mathcal{N}(u)| |\mathcal{N}(u)|} \]
Matrix Formulation
Aggregation 연산은 sparse matrix operation을 효율적으로 할 수 있다.
$\mathbf{H}^{(k)} = [\mathbf{h}_1^{(k)}, \dots, \mathbf{h}_{V}^{(k)}]^\top$ 이라 하면
$\sum_{u \in N(v)}\mathbf{h}_u^{(k)} = \mathbf{AH}^{(k)}$
대각행렬 $\mathbf{D}$가 $\mathbf{D} = Degree(v) = |N(v)|$이므로 $\mathbf{D}^{-1} = \cfrac{1}{|N(v)|}$
따라서
\[ \sum_{u \in N(v)} \cfrac{h_u^{(k-1)}}{|N(v)|} = H^{(k+1)} = D^{-1}AH^{(k)} \]

최종적으로 matrix form 으로 update function을 재작성하면
\[ H^{(k+1)} = \sigma \left( \tilde{A}H^{(k)}W_k^\top + H^{(k)}B_k^\top \right) \quad \text{where} \tilde{A} = D^{-1}A \]
실제 컴퓨팅 연산에서 $\tilde{A}$가 sparse matrix이므로 효율적으로 동작한다.
Note: 모든 GNN이 matrix form으로 작성할 수 있는 것은 아니다. aggregation function이 단순한 경우에만 가능하다.
Supervised Training
우리가 잘 아는 방법대로 training 하면 된다.
\[ \min_{\theta} \mathcal{L}(\mathbf{y}, f(\mathbf{z}_v)) \]
\[ \mathcal{L} = - \sum_{v \in V}y_v \log{(\sigma(z_v^\top \theta))} + (1-y_v)\log{(1-\sigma(z_v^\top \theta))} \]
e.g. drug-drug interaction network에서 이 drug(node)가 safe/toxic 한가? (node classification)
Unsupervised Training
similiar nodes have similar embeddings
\[ \mathcal{L} = \sum_{z_u, z_v}\mathrm{CE}(y_{u, v}, \mathrm{DEC}(z_u, z_v) ) \]
$u, \ v$가 similar하다면 $y_{u, v}=1$이다.
CE는 Cross Entropy이고 DEC는 Decoder이다. (e.g. inner product)
CNN vs GNN
CNN은 GNN의 특별한 구조로 생각할 수 있다. GNN에서 고정된 크기의 neighbor와 ordering을 가진 모델이라 할 수 있다.
그러나 CNN은 permutation invariant/equivariant 하지 않다.
'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| [CS224w] 5. A General Perspective on GNNs (1), 이론편 (0) | 2023.03.11 |
|---|---|
| [CS224w] 5. A General Perspective on GNNs (2), 아키텍처 (0) | 2023.03.10 |
| [CS224w] Colab 1 - Node Embeddings (1) | 2023.03.06 |
| [CS224W] 3. Node Embeddings (0) | 2023.01.28 |
| [CS224W] 2. Feature Engineering for ML in Graphs (0) | 2023.01.23 |



