출처: http://web.stanford.edu/class/cs224w/index.html
CS224W: Machine Learningn with Graphs
Complex domains (Social networks, internet, Knowledge Graphs, 3D shapes, etc) have a rich relational sturcture, whic can be represented as a relational graph.
Modern deep learning toolbox is designed for simple sequences and grids.
Not everything can be represented as a sequence or a grid.

NN을 이용하여 node의 이웃 node로부터 정보를 모은다(aggreate)
Representation Learning
node $u$ 를 $d$-차원으로 임베딩하여 비슷한 node는 $\mathbb{R}^d$ 공간에서 가까이 있게 한다.

Course Outline
- Traditional methods: Graphlets, Graph Kernels
- Node Embedding: DeepWalk, Node2Vec
- Graph Neural Network: GCN, GraphSAGE, GAT, Theroy of GNNs
- Knowledge graphs and reasoning: TransE, BetaE
- Deep generative models for graph: GraphRNN
- Applications to Biomedicin, Science, Technology
Classic Graph ML Tasks
크게 node-level, edge-level, subgraph(community)-level, graph-level 문제로 분류할 수 있다.
- Node classification
- user/item 유형화(categorize)
- Link prediction
- 두 node의 link가 있는지 예측
- Knowledge graph completion
- Graph classification
- 분자의 물성 예측
- Clustering
- Social circle detection
- Others
- Graph generation: 신약개발
- Graph evolution: 시뮬레이션
Examples of tasks
- Node-level: protain folding
- 아미노산의 배열만으로 3차원 단백질 구조를 예측
- DeepMind의 AlphaFold라는 AI 모델은 Spatial graph라는 아이디어
- node: 아미노산의 배열, edge: 두 아미노산의 유사성
- Edge-level: Recommender Systems
- user는 item과 상호작용한다는 아이디어에서 출발. 두 노드의 연관성을 예측
- node: user, items, edge: user-item interaction
- Edge-level: Drug Side Effects
- 많은 환자들은 여러 약을 동시에 복용한다. 약의 쌍이 주어지면 부작용을 예측해보자
- node: drug, protein. edge: interaction, query: 2개의 node(약, 단백직)이 주어지면 edge가 생성되는가?
- 부작용의 De novo를 예측하였고, 이중 몇개는 실제로 후대 연구에 밝혀짐
- Subgraph-level: Traffic Prediction
- ETA(Estimated Time of Arrival) 예측
- node: road segments, edge: connectivity
- 구글맵에서 사용된다고 알려져있다.
- Graph-level: Drug Discovery
- 항체는 작은 분자 그래프로 해석
- node: 원자. edge: 화학결합
- 신약 가능성이 높은 분자 구조 생성 또는 현존하는 분자들의 속성 최적화(?)
- Graph-level: Physics Simulation
- node: 입자, edge: 입자간 상호작용
- goal: graph가 어떻게 evolve할지 예측 (DeepMind의 기상 예측)
Choice of Graph Representation
$N$: object, node, vertex
$E$: interaction, link, edge
$G(N, E)$: system, network, graph
How to build a grpah?
- node는 무엇인가?
- edge는 무엇인가?
- 주어진 domain이나 문제 정의에 따라 적절한 network representation이 필요하다
| Undirected | Directed |
 |
 |
| symmetrical, reciprocal | arcs |
| collaborations, friendship(facebook) | phone calls, following(twitter) |
Heterogenous Graphs
노드가 다양한 타입을 가질 수 있다.
$$G = (V, E, R, T)$$
Node) $v_i \in V$
Edge) $(v_r, r, v_j) \in E$
Node Type) $T(v_i)$
Relation type) $r \in R$
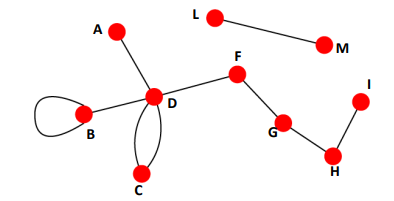
Node Degrees (노드의 차수)
$i$번째 노드의 차수를 $k_i$로 표현한다. directed network의 경우 in-degree, out-degree(진입차수, 진출차수)가 있고 $i$번째 노드의 진입/진출차수를 각각 $k_i^{in}, k_i^{out}$으로 표기한다.
- (무방향그래프) 평균차수 $\bar{k} = \cfrac{2E}{N}$
- (방향그래프) 평균차수 $\bar{k} = \cfrac{E}{N}$
- (방향그래프) $k_i = k_i^{in} + k_i^{out}$
- (방향그래프) $\overline{k^{in}} = \overline{k^{out}}$
- (방향그래프) source: $k^{in}=0$, sink: $k^{out} = 0$
Bipartite Graph (이분그래프)
모든 link에 연결된 두 노드가 각각 두개의 분리집합(disjoint set) $U$와 $V$의 원소일 때때, 주어진 그래프를 이분그래프라고한다. (같은 집합에 속한 노드는 link가 없다)

examples:
- authors-to-papers
- actors-to-movies
- users-to-movies
- recipes-to-ingredients
Representing Graphs: Adjacency Matrix(인접행렬)
$i$와 $j$가 연결괴어있으면 $A_{ij}=1$, 연결되어있지않으면 $A_{ij}=0$이다.
인접행렬은 희소행렬이다. (sparse)
real-world에서 network는 sparse하다. ($E << E_{max}$ OR $k << N-1$)
Connectivity
인접행렬의 몇몇 요소들은 block-diagonal form을 갖는다.
Graph Machine Learning Tools
PyG (Pytorch Geometric)
GraphGym
SNAP.PY
NetworkX
'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| [CS224w] 5. A General Perspective on GNNs (2), 아키텍처 (0) | 2023.03.10 |
|---|---|
| [CS224w] 4. Graph Neural Networks (0) | 2023.03.07 |
| [CS224w] Colab 1 - Node Embeddings (1) | 2023.03.06 |
| [CS224W] 3. Node Embeddings (0) | 2023.01.28 |
| [CS224W] 2. Feature Engineering for ML in Graphs (0) | 2023.01.23 |



