LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation
Motivation
shallow embeddings은 그 자체로 꽤 좋은 표현력(expressive)를 가진다.
노드 개수를 $N$, 임베딩 차원을 $D$라 하면
- shallow embedding: $O(ND)$
- GNN: O(D^2)
GNN의 파라미터는 충분하지 않을 수 있다
그러면 GNN으로 NGCF의 파라미터를 줄일 수 있을까? YES!
게다가 단순화(simplification)은 추천 성능을 향상시킬 수 있다.
LightGCN의 idea는 크게 3가지이다.
- 이분그래프에서의 인접행렬(adjacency matrix)
- GCN의 행렬 곱셈(matrix formulation)
- 비선형성을 제거하여 GCN을 단순화 (SGC for scalabel GNN에 처음 제시된 아이디어임)
Simplifying GCN
$\mathbf{R}$을 user-item의 상호작용이 저장된 행렬(user-item interaction matrix)이라고 하자.
$u$와 $v$가 상호작용이 있으면 $R_{uv}=1$이고, 상호작용이 없으면 $R_{uv}=0$이다.
user 개수와 item 개수를 각각 $M$, $N$이라 하면 $\mathbf{R} \in \mathbb{R}^{M \times N}$이다.
$\mathbf{R}$을 이용하여 adjacency matrix를 구성하면 (NGCF와 동일하게) 다음과 같다.
\[ \mathbf{A} = \begin{bmatrix} \mathbf{0} & \mathbf{R} \\ \bf{R}^\top & \mathbf{0} \end{bmatrix} \]
임베딩 행렬(embedding matrix)를 $\mathbf{E} \in \mathbb{R}^{(M + N) \times T}$라 하자. ($T$는 임베딩 차원)
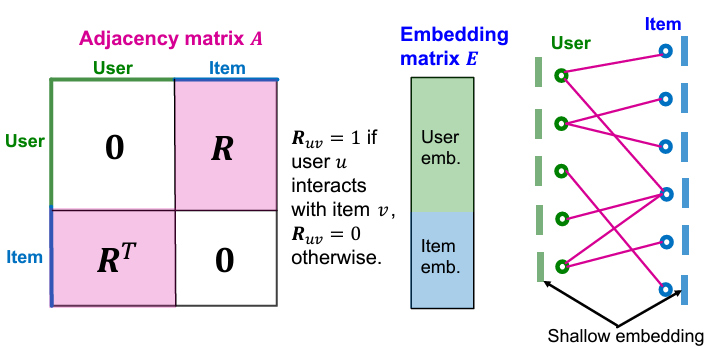
위 그림은 $\mathbf{A}$와 $\mathbf{E}$를 시각화한 것이다.
user를 초록색, item을 파란색으로 표시하였다.
그러면 Light Graph Convolution (LGC)는 다음과 같이 연산할 수 있다.
$\tilde{\mathbf{A}} = \mathbf{D}^{-\frac{1}{2}} \mathbf{AD}^{-\frac{1}{2}} $라 하면
\[ \mathbf{E}^{(k+1)} = \left( \mathbf{D}^{-\frac{1}{2}} \mathbf{AD}^{-\frac{1}{2}} \right) \mathbf{E}^{(k)} = \tilde{\mathbf{A}} \mathbf{E}^{(k)} \]
$\mathbf{D}$는 $\mathbf{A}$의 degree matrix이다. ($\mathbf{D} \in \mathbb{R}^{(M + N) \times (M + N)}$)
마지막으로 최종적으로 얻는 embedding matrix $\mathbf{E}$는 다음과 같다.
\begin{align} \mathbf{E} &= \alpha_0 \mathbf{E}^{(0)} + \alpha_1 \mathbf{E}^{(1)} + \cdots + \alpha_K \mathbf{E}^{(K)} \\ &= \alpha_0 \mathbf{E}^{(0)} + \alpha_1 \tilde{\mathbf{A}} \mathbf{E}^{(0)} + \cdots + \alpha_K \tilde{\mathbf{A}}^K \mathbf{E}^{(0)} \end{align}
$\alpha$는 hyperparameter이고, simplicity를 위해 LightGCN에서 uniform한 계수인 $\alpha_k = \frac{1}{K + 1}$을 사용한다.

Overview of LightGCN
 user-item interaction matrix $\mathbf{R}$로부터 인접행렬 $\mathbf{A}$를 정의한다. $\mathbf{A}$를 정규화하여(self-loop는 제거) $\tilde{\mathbf{A}}=\mathbf{D}^{-1/2} \mathbf{AD}^{-1/2}$를 구한다. 초기 임베딩 행렬 $\mathbf{E}$를 구한다. |
 $k=0, 1, \dots, K$동안 diffuse embedding을 구한다. \[ \mathbf{E}^{(k+1)} = \tilde{\mathbf{A}} \mathbf{E}^{(k)} \] |
 $K+1$개의 각 layer별 임베딩을 평균값을 취해 최종 임베딩 행렬을 구한다. \[ \mathbf{E} = \cfrac{1}{K+1} \left( \mathbf{E}^{(0)} + \mathbf{E}^{(1)} + \cdots + \mathbf{E}^{(K+1)} \right) \] |
 이렇게 구한 final embedding matrix를 통해 score function을 계산한다. |
Loss function은 BPR loss를 이용한다.
모델 파라미터는 $\mathbf{E}^{(0)}$뿐이므로 $\mathbf{E}^{(0)}$에 L2-regularization을 추가한다.

'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| [CS224W] GNN for RecSys (3) - NGCF (Neural Graph Collaborative Filtering) (1) | 2024.11.08 |
|---|---|
| [CS224W] GNN for RecSys (2) - Embedding-Based Models (0) | 2024.11.07 |
| [CS224W] GNN for RecSys (1) - Task and Evaluation (2) | 2024.11.06 |
| [논문리뷰] Deep Graph Infomax (DGI) (0) | 2024.06.18 |
| [Bayesian] Bayesian Linear Regression (베이지안 선형 회귀) (0) | 2024.05.08 |



