Embedding-Based Models, Surrogate Loss Functions, BPR Loss
Notation and Score Function
$U$를 모든 user의 집합, $V$를 모든 item의 집합, 그리고 $E$를 관찰한(observed) user-item 상호작용 집합이라 하자.
top-K item을 추천한다고 하자.
유저 $u$에게 추천할 item은 $\text{score}(u, v)$가 가장 큰 순서대로 $K$개의 item을 추천해주면 된다.
이때, 추천해줄 item은 이미 상호작용한 item은 제외해야한다. (excluding already interacted items)
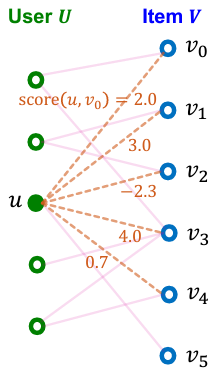
위 그림의 경우, 실선은 already interacted edge이고, 점선은 interaction되지 않은 edge이다.
$K=2$라 할 때 3번째 user $u$에게 추천할 item은 $\{ v_1, v_3 \} $이다.
$v_5$는 이미 상호작용하였으므로 추천에서 제외한다.
Embedding-Based Models
위의 추천시스템의 컨셉을 유지하면서 이제 embedding을 이용한 모델을 생각해보자.
각 $u, v$의 embedding vector를 $\mathbf{u}, \mathbf{v}$라 하고 $D$차원이라고 하자.
즉, $\mathbf{u}, \mathbf{v} \in \mathbb{R}^{D}$
score function은 paramter가 $\theta$이고 두 $D$차원 벡터를 입력받아 스칼라(score)를 출력한다.
즉, $f_{\theta}(\cdot, \cdot): \mathbb{R}^{D} \times \mathbb{R}^{D} \to \mathbb{R}$
이 embedding model은 다음 3개의 parameter를 가져야 한다.
- user embedding을 얻기 위한 encoder
- item embedding을 얻기 위한 encoder
- score function
이 model의 최적화는 Recall@K를 최대화 하는 방향으로 학습한다.
(당연히 미래의 unseen/test interaction에서도 Recall@K가 높기를 원한다)
Surrogate Loss Functions
문제는 recall@K는 미분가능한 함수가 아니기 때문에 gradient descent와 같은 최적화 방법을 이용할 수 없다.
여기서는 미분가능한 다른 함수를 이용하여 모델을 최적화한다. 이 함수를 대리손실함수라한다.
surrogate loss function(대리 손실 함수?)는 미분가능하며 원래 학습 목표와 잘 맞아야 한다.
여기서는 2개만 다룬다
- Binary loss
- Bayesian Personalized Ranking (BPR) loss
Binary Loss
positive/negative edge를 binary classification하는 접근법이다.
이때 positive edge는 observed/training user-item interaction으로 정의한다.
negative edge는 positive edge의 여집합이다.

그리고 training하는 동안 위 loss function은 mini-batch로도 최적화할 수 있다.
binary loss은 positive edge의 score는 높게, negative loss의 score는 낮게 학습한다.
이는 원래 목표인 recall@K의 값을 높이는데 도움이 된다.
그러나 binary loss에는 문제점이 있다.
모든 positive edge를 모든 negative edge보다 높은 score로 강요하기(push) 때문이다.
이는 recall 점수가 높아도 불필요한 패널티 모델 예측로 최적화할 수 있다.
이게 무슨소리? 아래 예시를 보자

2개의 user와 2개의 item이 있는 단순한 이분그래프이다.
Recall@1을 metric이라 하자.
현재 training중인 recall@1은 1.0으로 perfect하다. (최적화할 필요가 없음)
그러나 binary loss는 계속 penalize를 하려고 한다.
왜냐하면 negative edge에서 $(u_1, v_0)$의 score가 $(u_0, v_1)$의 score보다 높기 때문이다.
여기서 알 수 있는 것은 binary loss는 non-personalize한 접근방법이라는 것이다.
recall은 user마다 정의되므로 personalized metric이다.
non-personalized binary loss는 recall에 비해 지나치게 엄격한 metric이다.
따라서 바람직한 surrogate loss는 personalized manner가 있어야 한다.
BPR Loss
여담으로, bayesian이라는 용어는 loss 정의에 필수적인 것은 아니다. Rendle et al. 2009에서 parameter에 대한 Bayesian prior를 고려해야하지만 여기선 생략한다.
각 유저 $u^* \in U$에 대하여 rooted positive/negative edge를 정의하자.
마치 $u^*$를 tree의 root node로 생각하고, positive/negative edges에 속하는 edge만 따로 추출한다.
$E(u^*) \equiv \{ (u^*, v) \mid (u^*, v) \in E \} $
$E_{\text{neg}}(u^*) \equiv \{ (u^*, v) \mid (u^*, v) \in E_{\text{neg}} \}$
각 유저 $u^*$에 대하여 rooted positive edge의 score가 rooted negative edges보다 높도록 최적화한다.

Final BPR loss는 $\cfrac{1}{|U|} \sum_{u^* \in U} \text{Loss}(u^*)$ 이다.
위 식은 전체 gradient descent에서의 최적화 식이다.
그러나 deep learning에서 mini batch training을 적용하는 것이 시간을 절약하므로 식을 변형해보자
$U$의 부분집합 $U_{\text{mini}}$를 생각하자.
$u^*$로부터 1개의 positive item $v_{\text{pos}}$와 sampled negative items $V_{\text{neg}} = \{ v_{\text{neg}} \}$

이렇게 sample을 구한 후에 BPR loss에 넣으면 mini batch BPR loss이다.

Why Embedding Models Work?
사실 이러한 임베딩 방법은 Collaborative Filtering (CF)이 내재되어있다.
similar user는 similar item을 선호한다는 배경은 추천시스템의 기본 방법론중 하나이다.
저차원 임베딩 벡터는 모든 user-item의 상호작용을 모두 기억하지 못한다.
(단순히 모델이 user-item 상호작용을 외워서 예측하는 것이 아니다)
즉 임베딩 벡터는 user/item의 similarity를 capture할 수밖에 없다.
따라서 임베딩은 모델이 관찰하지 않은 unseed user-item 상호작용을 효과적으로 예측할 수 있다.
Limitations of Shallow Encoders
그러나 이러한 임베딩 방법 역시 단점이 있다.
우선 collaborative filtering은 user/item의 고유한 feature를 전혀 사용하지 않는다.
그러므로 model은 graph 구조를 직접적으로 학습하는 것이 아니다.
단순히 model은 implicit한 구조를 학습할 뿐이다.
모델은 오직 first-order graph structure만 capture하고 있다.
따라서 high-order (e.g. k-hop paths)와 같은 graph structure는 명시적으로 학습하지 않는다.
앞으로 이어지는 포스팅은 명시적으로 그래프 구조를 파악하면서 high-order graph structure도 포착하는 모델을 이용한 추천시스템이다.
그리고 이러한 모델은 GNN이 가능함을 앞서 공부했다.
GNN을 이용한 추천시스템 모델중 대표적으로 다음을 공부할 것이다
- Neural Graph Collaborative Filtering (NGCF)
- LightGCN (LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation)
- PinSAGE (Graph Convolutional Neural Networks for Web-Scale Recommender Systems)
'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| [CS224W] GNN for RecSys (4) - LightGCN (0) | 2024.11.09 |
|---|---|
| [CS224W] GNN for RecSys (3) - NGCF (Neural Graph Collaborative Filtering) (1) | 2024.11.08 |
| [CS224W] GNN for RecSys (1) - Task and Evaluation (2) | 2024.11.06 |
| [논문리뷰] Deep Graph Infomax (DGI) (0) | 2024.06.18 |
| [Bayesian] Bayesian Linear Regression (베이지안 선형 회귀) (0) | 2024.05.08 |



