GNN for Recommender Systems: Task and Evaluation
Preliminary
추천시스템은 기본적으로 이분그래프(bipartite graph)의 구조를 갖는다.
이분 그래프는 2개의 노드 종류를 갖는다: users, items
이분 그래프의 edge는 user와 item을 연결한다.
user-item의 상호작용(interaction)일 수도 있고, timestamp와 연관지을 수도 있다.
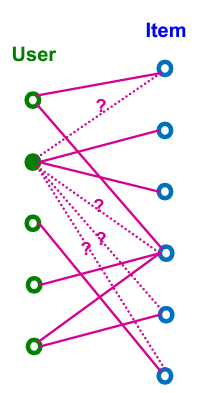
추천시스템의 목적은 다음과 같다.
과거의 user-item 상호작용이 주어질 때, 새로운 user-item 상호작용을 예측한다.
(보통 기존 user가 new item과 상호작용을 할지 말지)
이를 link prediction으로 환원하여 생각할 수 있다.
user와 item의 집합을 $U,\ V$라 하자.
$u \in U$, $v \in V$일 때, 우리는 실수값을 갖는 score function $f(u, v)$를 구현해야한다.
Modern RecSys
현대 추천시스템은 데이터가 너무 많기 때문에 모든 $u-v$ pair를 구할 수 없다.
보통 2-stage process로 추천시스템을 구현한다.
- 후보쌍 생성 (cheap, fast)
- 랭킹 계산 (slow, accurate)
각 user마다 $K$개의 item을 추천해준다고 하자.
추천이 효과적이려면 $K$는 전체 item 개수보다 현저히 적어야 한다.
일반적으로 $10 \le K \le 100$ 이다. (item 개수가 수십억 단위)
이렇게 top-K 추천했을 때, 실제로 얼마나 positive item을 포함하는지가 목표이다.
(positive item: 미래에 실제 user가 상호작용할 item)
이러한 평가지표를 Recall@K라고 한다.
※ Precision@K, Recall@K, F1@K, MAP, NDCG 등 여러가지 metric을 사용할 수 있다.
Recall@K
각 user $u$에 대하여 $P_u$와 $R_u$를 구해보자.
$P_u$: user $u$가 미래에 상호작용할 positive item의 집합
$R_u$: model이 $u$에게 추천해주는 item 집합. top-K 추천시스템이라면 $|R_u|=K$ 이다.
이때, Recall@K는 다음과 같이 계산한다.
\[ \text{Recall@}K = \cfrac{P_u \cap R_u}{|P_u|} \]

final Recall@K는 모든 user의 평균값을 이용한다.
GNN은 user와 item(product)를 embedding한다.
LLM은 textify한 후에 embedding을 한다.
"Do Large Language Models make accurate personalized recommendations?"에 따르면, GNN이 LLM보다 개인화 추천시스템에 더 정확하다고 한다.
※ LLM과 GNN 모두 연구가 활발하므로 앞으로 내용이 바뀔지로 모른다.
'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| [CS224W] GNN for RecSys (3) - NGCF (Neural Graph Collaborative Filtering) (1) | 2024.11.08 |
|---|---|
| [CS224W] GNN for RecSys (2) - Embedding-Based Models (0) | 2024.11.07 |
| [논문리뷰] Deep Graph Infomax (DGI) (0) | 2024.06.18 |
| [Bayesian] Bayesian Linear Regression (베이지안 선형 회귀) (0) | 2024.05.08 |
| Double Descent: new approach of bias-variance trade-off (0) | 2024.03.03 |



