[Clustering] BIRCH Algorithm

 

Basic Concepts of BIRCH

BIRCH (Balanced Iterative Reducing and Clustering Using Hierarchies)

 

Clustering Feature Tree(CF-Tree)를 점진적으로 증가시켜 데이터의 계층을 구성한다.

(1) 데이터를 scan하여 CF tree를 구성한다.

(2) arbitrary clustering 알고리즘을 이용하여 CF-tree의 leaf node를 cluster로 한다.

 

Scales Linearly

single scan만으로도 좋은 클러스터링이 가능하다.

약간의 추가적인 scan으로 더 좋은 퀄리티 향상이 가능하다.

전체적인 시간복잡도는 $O(n)$ 이다.

 

Weakness

numeric data만 적용할 수 있다.

데이터 순서에 민감하다. (sensitive to the order of the data record)

Similarity Metric

$X$ instance를 $\{ \vec{X}_i  \}$라 할 때 다음과 같이 Centroid, Radius, Diameter를 정의하자.

 

Centroid

$\vec{C} = \frac{1}{N}\sum_{i=1}^{N} \vec{X}_i$

Note: 논문에서는 centroid를 $\vec{C}$라 하지 않고 $\vec{X0}$로 표기하였다.

 

Radius: centroid로부터의 평균거리

$R = \left( \frac{1}{N}\sum_{i=1}^{N}(\vec{X}_i - \vec{C})^2 \right)^{1/2} = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(\vec{X}_i - \vec{C})^2}$

 

Diameter: pair-wise의 평균거리

$D = \left( \frac{1}{N(N-1)}\sum_{i=1}^{N} \sum_{j=1}^{N} (\vec{X}_i - \vec{X}_j)^2  \right)^{1/2} = \sqrt{\frac{1}{N(N-1)}\sum_{i=1}^{N} \sum_{j=1}^{N} (\vec{X}_i - \vec{X}_j)^2}$

 

이를 바탕으로 $1$번 클러스터와 $2$번 클러스터의 거리(및 유사도)를 5가지로 정의한다.

 

Centroid Euclidean Distance $D0 = \sqrt{(\vec{C}_1 - \vec{C}_2)^2}$

Centroid Manhattan Distance $D1 = |\vec{C}_1 - \vec{C}_2| = \sum_{i=1}^{d} |\vec{C}_1^{(i)} - \vec{C}_2^{(i)}|$

Average inter-cluster $D2 = \sqrt{\frac{1}{N_1 N_2} \sum_{i=1}^{N_1} \sum_{j=N_1 + 1}^{N_1 + N_2} (\vec{X}_i - \vec{X}_j)^2 }$

Average intra-cluster $D3 = \sqrt{\frac{1}{(N_1+N_2)(N_1 + N_2 - 1)} \sum_{i=1}^{N_1 + N_2} \sum_{j=1}^{N_1 + N_2} (\vec{X}_i - \vec{X}_j)^2 }$

Variance increases $D4 = \sqrt{\sum_{k=1}^{N_1+N_2}(\vec{X}_k - \frac{\sum_{l=1}^{N_1 + N_2}\vec{X}_l}{N_1 + N_2})^2 - \sum_{i=1}^{N_1}(\vec{X}_i - \frac{\sum_{l=1}^{N_1} \vec{X}_l}{N_1})^2 - \sum_{j=N_1+1}^{N_1+N_2}(\vec{X}_j - \frac{\sum_{l=N_1+1}^{N_1+N_2}\vec{X}_l}{N_2} )^2 }$

반응형

Clustering Feature

BIRCH 알고리즘은 data set을 scan할 때 CF tree (Clustering Feature tree)를 만든다.

각 CF tree의 entry는 3-tuple로 이루어져있다. $(N, LS, SS)$ ($LS$는 linear sum을, $SS$는 sum of square이다.)

이때 $N$은 data point의 개수, $LS = \sum_{i=1}{N}\vec{X}_i$, $SS=\sum_{i=1}^{N} \vec{X}_i^2$

Note: $LS$는 벡터고, $SS$는 스칼라가 된다.

Example of Clustering Feature (CF)

Properties of Clustering Feature

CF는 몇가지 성질이 있는데 이는 이후 CF-tree를 만들 때 계산이 용이하다.

(1) CF entry는 compact하다. (storage 측면에서 매우 효율적이다)

(2) CF entry는 $D_0 \sim D_4$를 계산하기에 충분한 정보를 담고 있다.

(3) CF Additivity Theorem: $CF_1 + CF_2 = (N_1 + N_2,\ \vec{LS}_1 + \vec{LS}_2,\ SS_1 + SS_2)$

 

$C = \cfrac{\overrightarrow{LS}}{N},\ R = \sqrt{\cfrac{SS}{N} - (\cfrac{\overrightarrow{LS}}{N})^2},\ D = \sqrt{\cfrac{2N(SS) - 2(LS)^2}{N(N-1)}}$

CF-Tree

• CF-tree는 height-balanced tree이다. (height-balanced tree in which each leaf node contains a sub-cluster)
  • non-leaf node는 children을 갖는다.
  • non-leaf node는 children의 모든 CF의 합이다.
• CF-tree는 2개의 parameter를 갖는다.
  • Branching factor ($B$): children의 최대 개수. (non-leaf node는 최대 $B$개의 entry $[CF_i, child_i]$를 갖는다.)
  • Threshold ($T$): leaf node에 저장되는 sub-cluster의 max diameter. $T$가 커지면 tree는 작아진다.

Example of CF-Tree with $B=7,\ L=6$

BIRCH Algorithm

BIRCH clustering algorithm은 4개의 phase로 구성된다.

BIRCH Algorithm Overview

Phase 1: Building a CF-Tree

main task는 scan all data, build an initial in-memory CF tree, recycling space on disk. 이다.

초기 threshold $T$에 기반하여 데이터를 scan한다. 만일 out of memory 이슈가 발생하면 $T$ 값을 증가하여 다시 CF tree를 구성한다. 이때 기존 tree에 다시 leaf entry를 삽입하기 때문에(re-insertring the leaf entries of the old tree) 데이터를 다시 scan하지 않고도 새로운 tree를 만들 수 있다.

Note: B+-tree를 구성하는 방법과 유사하다.

1. 각 data point에 대하여, CF root node와 비교하여 가장 유사한(distance가 작은) root node를 찾는다. 
2. 해당 root node에서 descend down하여 non-leaf node와도 똑같이 비교한다.
3. 해당 non-leaf node에서 descend down하여 leaf node에서도 똑같이 비교한다.
4. new data point를 포함한 leaf node의 $R$(radius)와 $T$의 관계에 따라 달라진다.
   1. $R \le T$: new data point는 해당 leaf node에 추가되고, leaf와 parent CF의 값 역시 update
   2. $R > T$: 새로운 leaf node가 생성되고 거기에 new data point 추가. parent CF update.
   3. 4-2를 했다면, $B$에 맞추어서 split 할 수도 있다.

Control Flow of Phase 1

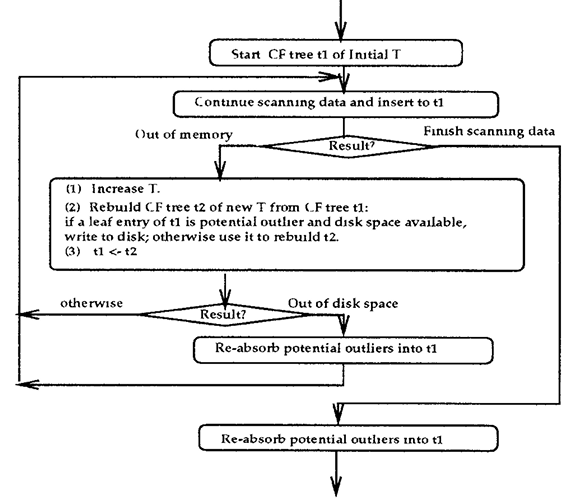
Phase 3: Global Clustering

CF tree의 leaf node가 cluster가 된다.

 

Summary of BIRCH

Concerns

• sensitive to insertion order
• leaf node의 size가 고정되어있기 때문에, cluster는 natural하지 않을 수 있다.
• radius, diameter 때문에 cluster는 spherical할 경향이 있다. (spherical shape가 아니라면 BIRCH가 잘 동작하지 않을 수 있다.)

 

Summary

• data space is usually not uniformly occupied. (not every data is equally importance for clustering)
• I/O cost를 최소화(efficiency 향상)하는 대신에 memory usage는 최대화(accuracy 향상)한다.

 

참고

BIRCH: An Efficient Data Clustering Method for Very Large Databases. Tian Zhang, Raghu Ramakrichnam, Miron Livny.