Setup
# Start from importing necessary packages.
import warnings
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from IPython.display import display
from sklearn import metrics # for evaluations
from sklearn.datasets import make_blobs, make_circles # for generating experimental data
from sklearn.preprocessing import StandardScaler # for feature scaling
from sklearn.cluster import KMeans
from sklearn.cluster import DBSCAN
# make matplotlib plot inline (Only in Ipython).
warnings.filterwarnings('ignore')
%matplotlib inline
앞선 포스팅에서는 파이썬으로 k-means과 k-means++ 알고리즘을 이용한 클러스터링을 살펴봤다.
그러나 이론에서 살펴보았듯이, k-means 알고리즘은 크게 3가지 단점이 있다.
- 직접 적절한 $k$를 지정해야한다.
- Noisy data와 Outlier에 영향을 많이 받는다.
- Non-convex 데이터에서는 global minimum이 보장되지 않는다.
이번 포스트에서는 직접 위 3가지 사례를 살펴보고, 어떻게 (최대한) 해결하는 방법도 소개한다.
Drawback1: Need to choose a right number of clusters
3개의 클러스터 데이터에 대하여 n_clusters=2로 클러스터링해보자.
# Generate data.
X, y = make_blobs(n_samples=1000,
n_features=2,
centers=3,
random_state=170)
# Plot the data distribution.
plt.scatter(X[:,0], X[:,1], c=y)
# Run k-means on non-spherical data.
y_pred = KMeans(n_clusters=2, random_state=170).fit_predict(X)
# Plot the predictions.
plt.scatter(X[:,0], X[:,1], c=y_pred)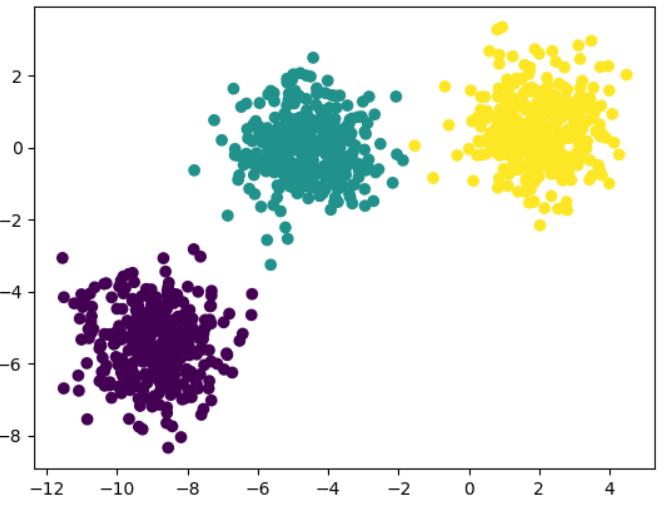
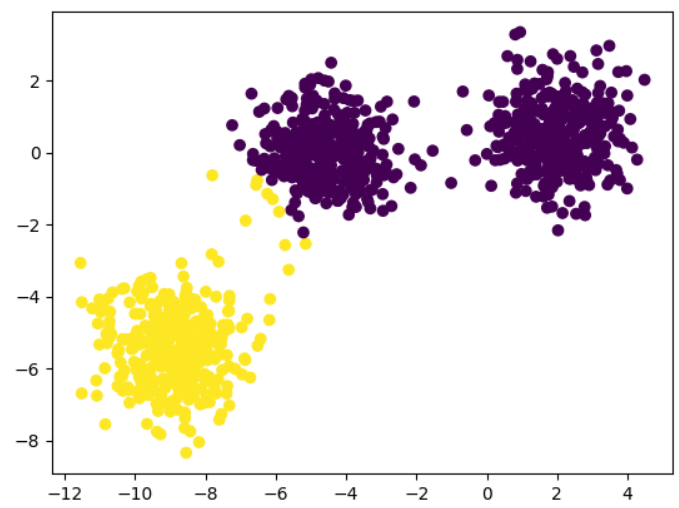
Solution: Measuring cluster quality to determine the number of clusters
잘못된 n_clusters로 인한 클러스터링을 방지하기 위해 cluster quality를 나타내는 지표를 이용할 수 있다.
supervised/unsupervised method가 있다.
Supervised Method
- Homogeneity - 각 클러스터는 하나의 class만을 member로 한다.
- Completeness - 같은 class인 모든 member는 같은 cluster로 매핑되어야 한다.
사이킷런 metrics 안에 이를 계산하는 모듈이 존재한다.
kmeans = KMeans(n_clusters=n_clusters, random_state=10)
y_pred = kmeans.fit_predict(X)
homogeneity = metrics.homogeneity_score(y, y_pred)
completeness = metrics.completeness_score(y, y_pred)
Unsupervised Method (Sihouette Coefficient, 실루엣 계수)
Sihouette Coefficient($s(x_i)$)는 compactness와 separation을 측정하는 지표이다. 실루엣 계수를 이용하면 적절한 개수의 클러스터 수를 구할 수 있다. mean intra-cluster distance($a(x_i)$)와 mean nearest-cluster distance($b(x_i)$) 를 이용한다.
- Mean intra-cluster distance, $a(x_i)$
- 클러스터의 compactness를 평가하는 지표이다. 데이터 포인트 $x_i$에 대하여 자신의 클러스터내의 ($x_i$ 자신을 제외한) 모든 data point와의 평균거리를 계산한다. 작을수록 좋다.
- $a(x_i) = \cfrac{\sum_{x_k \in C_j,\ k \neq i} D(x_i, x_k) }{\left\vert C_j \right\vert - 1}$
- Mean nearest-cluster distance, $b(x_i)$
- $x_i$가 다른 cluster와 얼마나 떨어져 있는지 평가하는 지표이다. $x_i$를 포함하지 않는 모든 클러스터에 대하여 모든 점과의 평균거리를 구한다. 다른 클러스터와의 거리이므로 클수록 좋다.
- $b(x_i) = \underset{C_j:\ 1 \leq j \leq k,\ x_i \notin C_j}{\min} \left\{ \cfrac{\sum_{x_k \in C_j} D(x_i, x_k) }{\left\vert C_j \right\vert } \right\}$
- Silhouette Coefficient
- $s(x_i) = \cfrac{b(x_i) - a(x_i)}{\max \{ a(x_i), b(x_i) \}}, \quad -1 \leq s(x_i) \leq 1$
- $a(x_i)$는 작을수록, $b(x_i)$는 클수록 좋으므로 $s(x_i)$가 $1$에 가까울 수록 cluster quality가 좋다.
사이킷런 metrics 안에 실루엣 계수를 구하는 모듈이 존재한다.
kmeans = KMeans(n_clusters=n_clusters, random_state=10)
y_pred = kmeans.fit_predict(X)
s = metrics.silhouette_samples(X, y_pred)
s_mean = metrics.silhouette_score(X, y_pred)
이제 실루엣 계수를 이용하여 적절한 클러스터 개수 $k$를 구해보자.
# Generate data.
# This particular setting has one distinct cluster and 3 clusters placed close together.
X, y = make_blobs(n_samples=500,
n_features=2,
centers=4,
cluster_std=1,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1)
# Plot the data distribution.
plt.scatter(X[:,0], X[:,1], c=y)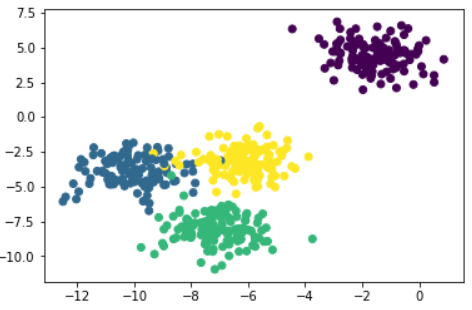
# List of number of clusters
range_n_clusters = [2, 3, 4, 5, 6]
# For each number of clusters, perform Silhouette analysis and visualize the results.
for n_clusters in range_n_clusters:
# Perform k-means.
kmeans = KMeans(n_clusters=n_clusters, random_state=10)
y_pred = kmeans.fit_predict(X)
# Compute the cluster homogeneity and completeness.
homogeneity = metrics.homogeneity_score(y, y_pred)
completeness = metrics.completeness_score(y, y_pred)
# Compute the Silhouette Coefficient for each sample.
s = metrics.silhouette_samples(X, y_pred)
# Compute the mean Silhouette Coefficient of all data points.
s_mean = metrics.silhouette_score(X, y_pred)
# For plot configuration -----------------------------------------------------------------------------------
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(18, 7)
# Configure plot.
plt.suptitle('Silhouette analysis for K-Means clustering with n_clusters: {}'.format(n_clusters),
fontsize=14, fontweight='bold')
# Configure 1st subplot.
ax1.set_title('Silhouette Coefficient for each sample')
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
ax1.set_xlim([-1, 1])
ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])
# Configure 2st subplot.
ax2.set_title('Homogeneity: {}, Completeness: {}, Mean Silhouette score: {}'.format(homogeneity,
completeness,
s_mean))
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
# For 1st subplot ------------------------------------------------------------------------------------------
# Plot Silhouette Coefficient for each sample
cmap = cm.get_cmap("Spectral")
y_lower = 10
for i in range(n_clusters):
ith_s = s[y_pred == i]
ith_s.sort()
size_cluster_i = ith_s.shape[0]
y_upper = y_lower + size_cluster_i
color = cmap(float(i) / n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper), 0, ith_s,
facecolor=color, edgecolor=color, alpha=0.7)
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
# Plot the mean Silhouette Coefficient using red vertical dash line.
ax1.axvline(x=s_mean, color="red", linestyle="--")
# For 2st subplot -------------------------------------------------------------------------------------------
# Plot the predictions
colors = cmap(y_pred.astype(float) / n_clusters)
ax2.scatter(X[:,0], X[:,1], c=colors)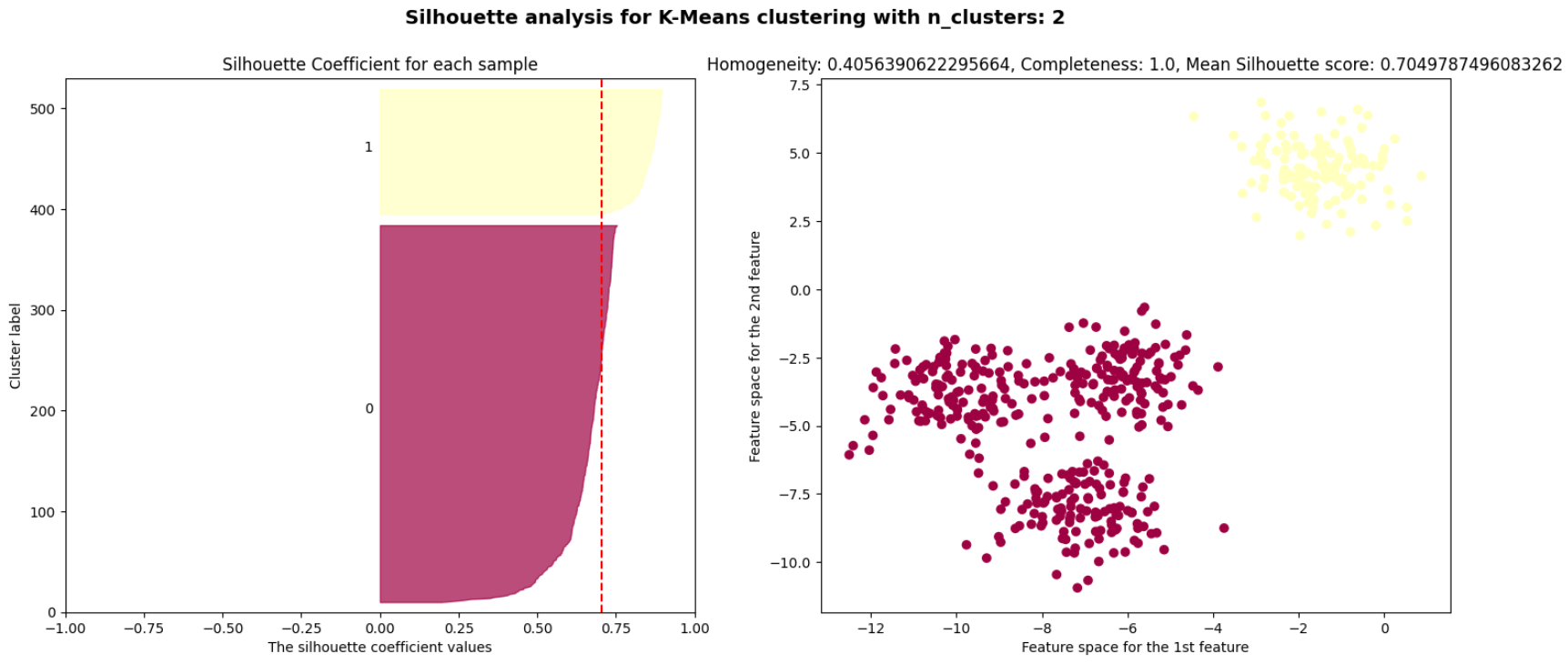
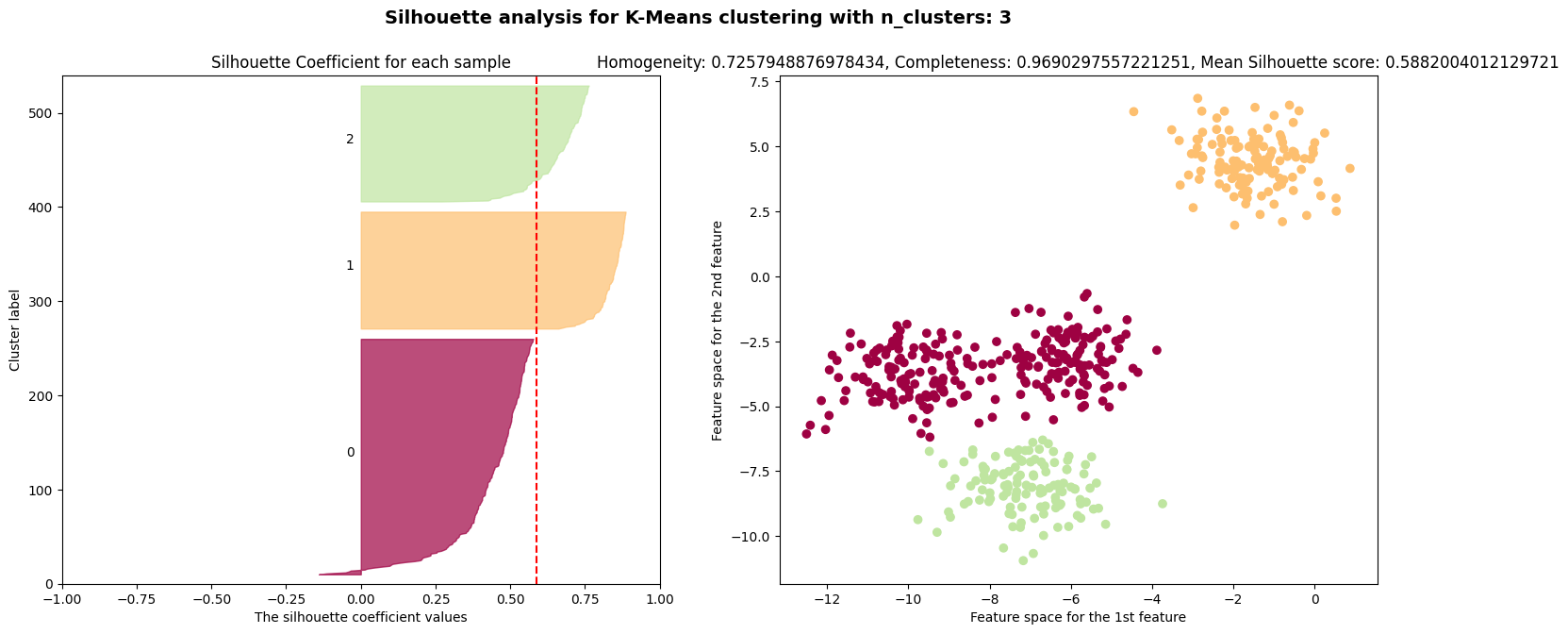
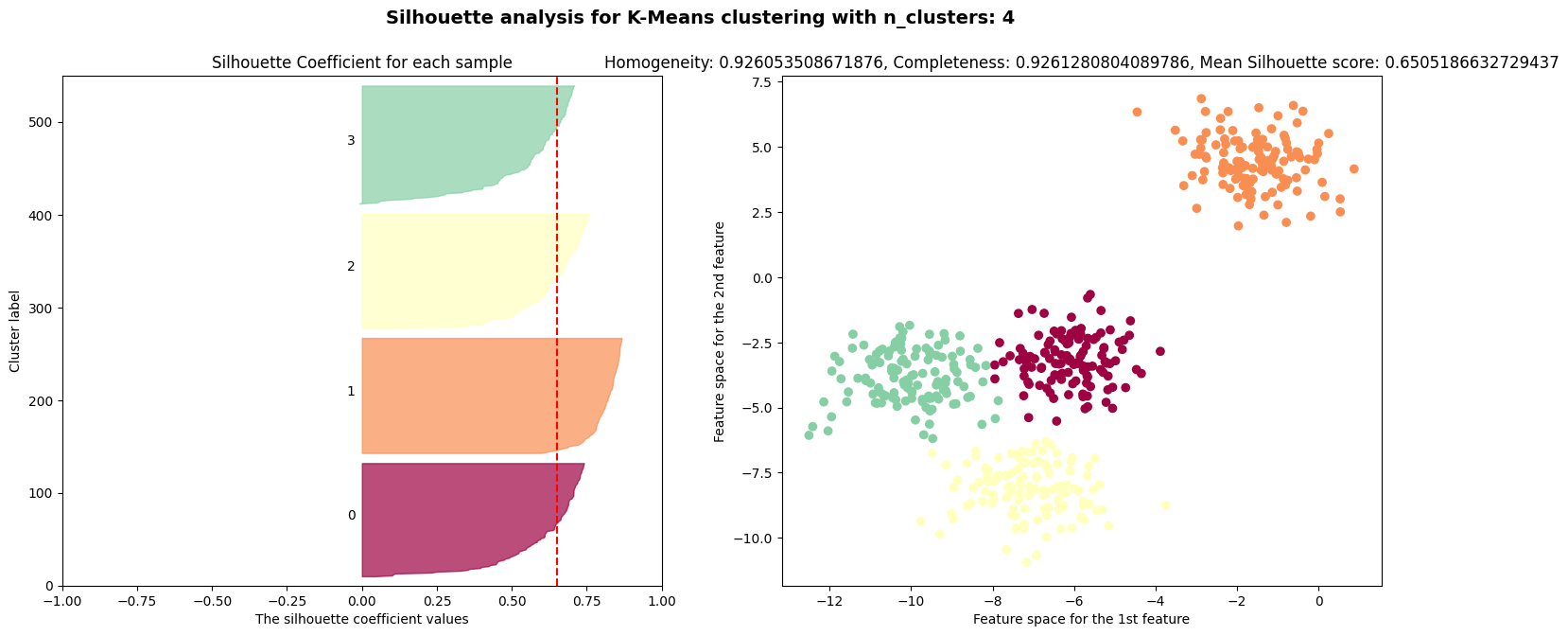
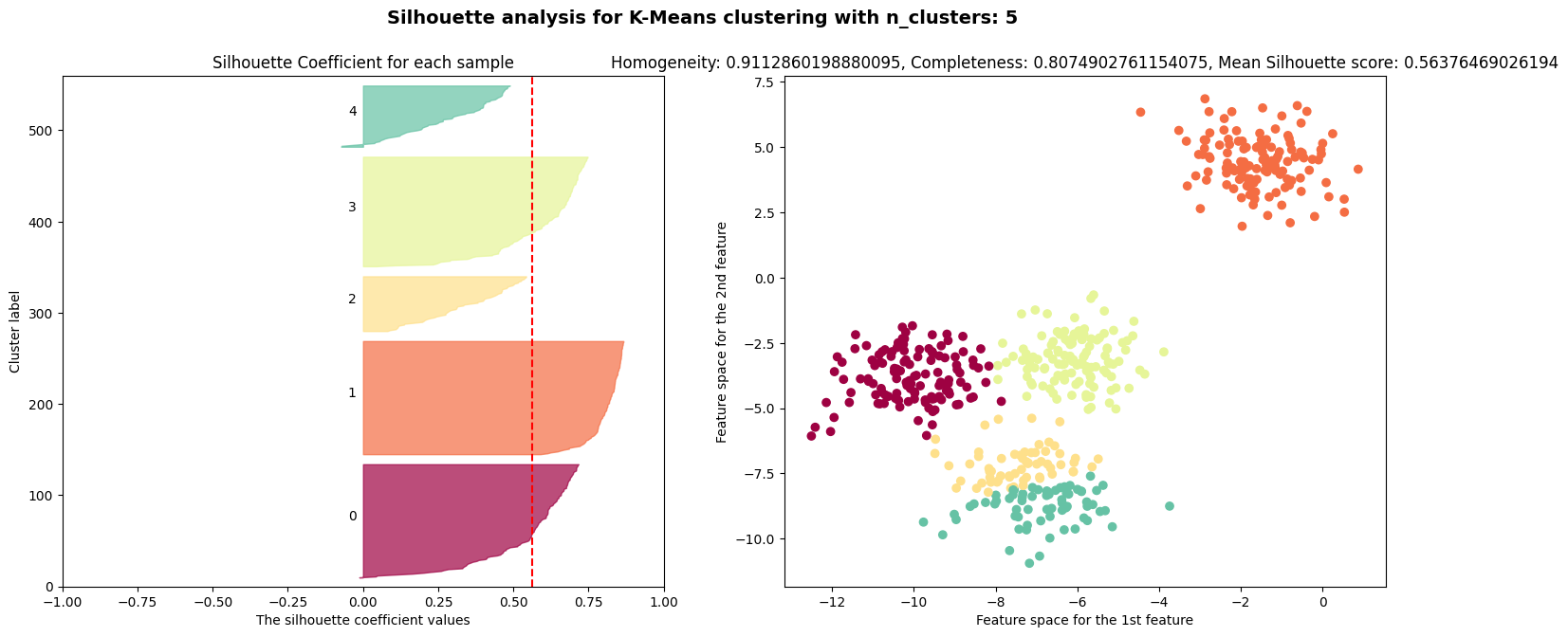
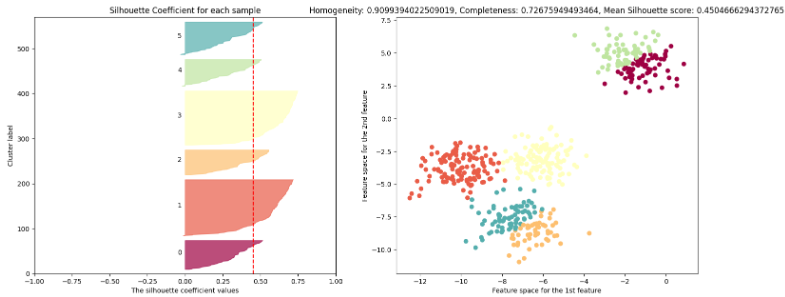
$k=2$인 경우에는 실루엣 계수가 $0.7$, $k=4$인 경우에는 실루엣 계수가 $0.65$로 높은 편이다.
실루엣 계수는 $k=3, 5, 6$인 경우에 나쁜 클러스터 개수임을 나타낸다.
Drawback2: Cannot handle noise data and outliers
4개의 클러스터 데이터를 생성하자. (위의 코드와 동일하다)
# Generate data.
# This particular setting has one distinct cluster and 3 clusters placed close together.
# (Same as the above example)
X, y = make_blobs(n_samples=500,
n_features=2,
centers=4,
cluster_std=1,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1)
# Perform k-means with n_clusters=4
kmeans = KMeans(n_clusters=4, random_state=10)
y_pred = kmeans.fit_predict(X)
# Plot the prediction
plt.scatter(X[:,0], X[:,1], c=y_pred)
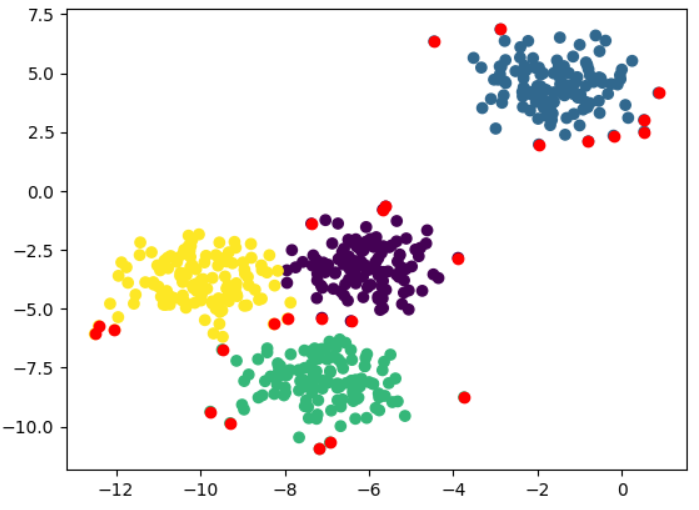
Solution: Use a distance threshold to detect noise data and outliers
거리가 threshold 이상이면 이상치로 판단하는 방법을 적용해볼 수 있다.
\[ threshold = \cfrac{1}{C_j}\sum_{k=0, k \neq i}^{\left\vert C_j \right\vert}D(x_k, c_j) \]
- $C_j$: $j$번째 클러스터
- $c_j$: $j$번째 클러스터의 centroid
- $x_i$: (관심이 되는) data point
# Ratio for our distance threshold, controlling how many outliers we want to detect.
distance_threshold_ratio = 2.0
# Plot the prediction same as the above.
plt.scatter(X[:,0], X[:,1], c=y_pred)
# For each ith cluster, i=0~3 (we have 4 clusters in this example).
for i in [0, 1, 2, 3]:
# Retrieve the indexs of data points belong to the ith cluster.
# Note: `np.where()` wraps indexs in a tuple, thus we retrieve indexs using `tuple[0]`
indexs_of_X_in_ith_cluster = np.where(y_pred == i)[0]
# Retrieve the data points by the indexs
X_in_ith_cluster = X[indexs_of_X_in_ith_cluster]
# Retrieve the centroid.
centroid = kmeans.cluster_centers_[i]
# Compute distances between data points and the centroid.
# Same as: np.sqrt(np.sum(np.square(X_in_ith_cluster - centroid), axis=1))
# Note: distances.shape = (X_in_ith_cluster.shape[0], 1). A 2-D matrix.
centroid.shape = (1,-1)
distances = metrics.pairwise.euclidean_distances(X_in_ith_cluster, centroid)
# Compute the mean distance for ith cluster as our distance threshold.
distance_threshold = np.mean(distances)
# Retrieve the indexs of outliers in ith cluster
# Note: distances.flatten() flattens 2-D matrix to vector, in order to compare with scalar `distance_threshold`.
indexs_of_outlier = np.where(distances.flatten() > distance_threshold * distance_threshold_ratio)[0]
# Retrieve outliers in ith cluster by the indexs
outliers = X_in_ith_cluster[indexs_of_outlier]
# Plot the outliers in ith cluster.
plt.scatter(outliers[:,0], outliers[:,1], c='r')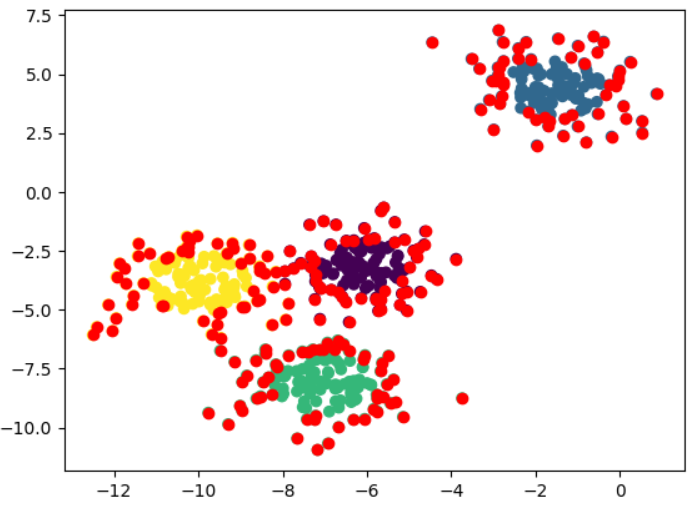
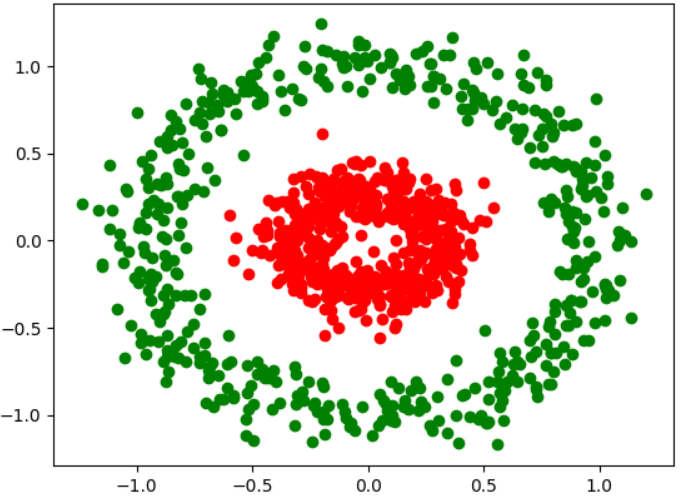
Drawback 3: Cannot handle non-spherical data
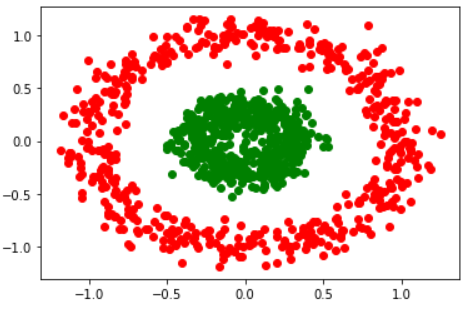
concentrici circle은 두 집합의 mean이 거의 같기 때문에, k-mean 알고리즘을 적용하면 (n_cluster를 제대로 지정해도) 클러스터링이 의도대로 되지 않는다.
# Generate non-spherical data.
X, y = make_circles(n_samples=1000, factor=0.3, noise=0.1)
# Plot the data distribution. (Here's another way to plot scatter graph)
plt.plot(X[y == 0, 0], X[y == 0, 1], 'ro')
plt.plot(X[y == 1, 0], X[y == 1, 1], 'go')
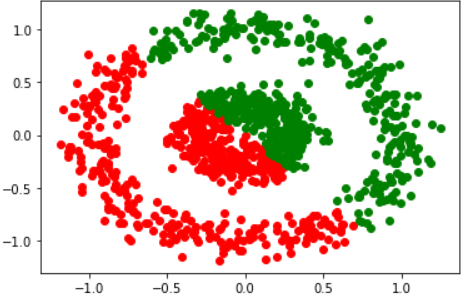
# Run k-means on non-spherical data.
y_pred = KMeans(n_clusters=2, random_state=170).fit_predict(X)
# Plot the predictions.
plt.plot(X[y_pred == 0, 0], X[y_pred == 0, 1], 'ro')
plt.plot(X[y_pred == 1, 0], X[y_pred == 1, 1], 'go')
# Print the evaluations
print('Homogeneity: {}'.format(metrics.homogeneity_score(y, y_pred)))
print('Completeness: {}'.format(metrics.completeness_score(y, y_pred)))
print('Mean Silhouette score: {}'.format(metrics.silhouette_score(X, y_pred)))
'''
Homogeneity: 0.0001413892985654956
Completeness: 0.00014138970653022453
Mean Silhouette score: 0.28939146559033435
'''
Solution: Using feature transformation or extraction techniques makes data clusterable
만일 우리가 데이터 모양이 concentric circle임을 알고있다면, 우리는 직교좌표계를 극좌표로 바꾸어서 새로운 좌표계에서 클러스터링을 할 수 있다. (각도 세타는 중요하지 않게 된다)
일반적인 방법으로는 Kernel PCA를 사용하여 linearly separable한 공간으로 project하거나, 다른 클러스터링 알고리즘(DBSCAN 등)을 고려할 수 있다. (DBSCAN을 이용하는 방법은 다른 포스팅에서 소개하겠다.)
Cartesian to Polar coordinates
직교좌표계를 극좌표로 변환한 후 극좌표계에서 클러스터링을 한 수 원래 좌표계에 cluster id를 매핑한다.
def cart2pol(x, y):
radius = np.sqrt(x**2 + y**2)
theta = np.arctan2(y, x)
return radius, theta
X_transformed = np.zeros_like(X)
# Convert cartesian (x-y) to polar coordinates.
X_transformed[:,0], _ = cart2pol(X[:,0], X[:,1])
# Only use `radius` feature to cluster.
y_pred = KMeans(n_clusters=2).fit_predict(X_transformed)
plt.plot(X[y_pred == 0, 0], X[y_pred == 0, 1], 'ro')
plt.plot(X[y_pred == 1, 0], X[y_pred == 1, 1], 'go')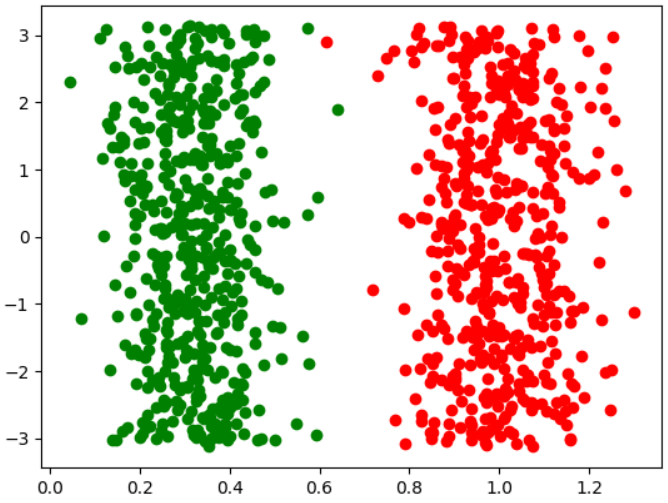
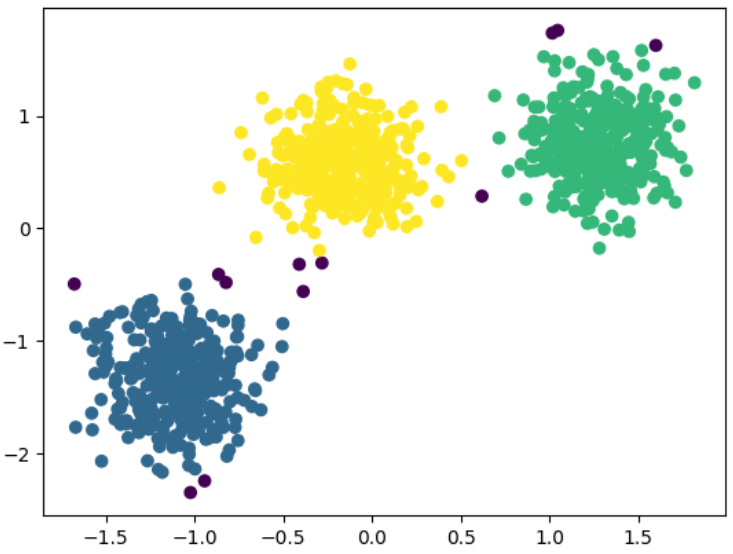
DBSCAN
DBSCAN에 대한 자세한 설명은 density-based methods에서 다룬다.
여기서는 간단히 파이썬 코드를 실행하는 방법만 소개한다.
DBSCAN은 대체로 eps와 min_samples라는 2개의 인자를 조절하여 클러스터링한다.
# Generate data with 3 centers.
X, y = make_blobs(n_samples=1000,
n_features=2,
centers=3,
random_state=170)
# Standardize features to zero mean and unit variance.
X = StandardScaler().fit_transform(X)
# Perform DBSCAN on the data
y_pred = DBSCAN(eps=0.3, min_samples=30).fit_predict(X)
# Plot the predictions
plt.scatter(X[:,0], X[:,1], c=y_pred)
# Print the evaluations
print('Number of clusters: {}'.format(len(set(y_pred[np.where(y_pred != -1)]))))
print('Homogeneity: {}'.format(metrics.homogeneity_score(y, y_pred)))
print('Completeness: {}'.format(metrics.completeness_score(y, y_pred)))
print('Mean Silhouette score: {}'.format(metrics.silhouette_score(X, y_pred)))
'''
Number of clusters: 3
Homogeneity: 0.9820397966048766
Completeness: 0.937810961939573
Mean Silhouette score: 0.6798548805414468
'''
Drawback 4: Cannot to handle categorical data
k-mean 알고리즘은 mean을 계산하기 때문에, (평균이 정의되지 않는) categoricla data에는 적용할 수 없다.
kmodes 알고리즘을 이용할 수 있다. (k-modes 알고리즘을 사용하는것은 생략)
Summary
- choosing number of clusters
- supervised measure
- Homogeneity
- Completeness
- unsupervised measure
- Sihouette Coefficient
- supervised measure
- noisy data & outliers
- distance threshold
- non-spherical data
- feature transform
- DBSCAN (density-based algorithm)
- categorical data
- can not compute mean; can not apply
- kmodes
'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| [Clustering] BIRCH Algorithm (0) | 2023.05.23 |
|---|---|
| [Clustering] Hierarchical Clustering (계층적 군집화) (0) | 2023.05.22 |
| [Clustering] K-means Clustering in Python (K-means 알고리즘) (0) | 2023.05.20 |
| [Clustering] Model-based Methods, Expectation Maximization (EM) (0) | 2023.05.19 |
| [Clustering] Partitioning Methods, K-Means Clustering, PAM, k-Medoids Clustering (0) | 2023.05.18 |



