[Clustering] Density-Based Methods, DBSCAN

 

Basic Concept of Density-Based Clustering

Major features

• 임의의 모양에 대한 clustering이 가능 (arbitrary shape)
• noise 조절
• 1번만 조회 (one scan)
• 종료 조건으로 density parameter가 필요함

density-based clustering으로 DBSCAN, OPTICS, DENCLUE, CLIQUE 등이 있고 DBSCAN에 대하여 알아보자.

 

DBSCAN

Density-Based Spatial Clustering of Applications with Noise

DBSCAN 알고리즘은 2014 KDD test of time award를 수상했다.

• arbitrary shape
• robust to noise
• scales well to large databases

Two parameters

Eps (Epsilon): Maximum radius of the neighborhood

MinPts (Min-Points): eps-neighborhood 안에 있어야 하는 point의 최소 개수

 

eps-neighborhood은 다음과 같이 집합의 형태로 표기한다.

\[ N_{eps}(p) = \{ q \in D \mid dist(p, q) \le Eps \} \]

 

Directly density-reachable (직접 밀도 도달가능)

$p$가 두 조건($p$가 $q$의 반경안에 있고, $q$가 core point)을 만족하면 directly density-reachable 하다고 한다.

아래 그림을 예시로 들면, (1) $p$는 $q$의 이웃반경 안에 존재하고, (2) $N(q)$의 크기는 minpoint=5 보다 크기 때문에 $q$는 core-point이다. 따라서 $p$는 $q$로부터 직접밀도 도달가능한 관계이다.

Directly density-reachable

• $p \in N_{eps}(q)$
• Core Point Condition: $\left| N_{eps}(q) \right| \ge MinPts$

Density-reachable (밀도 도달가능)

$q=p_1, p_2, \dots, p_{n-1}, p_n=p$에 대하여 $p_{i+1}$이 $p_{i}$로부터 직접밀도도달가능하면, $p$는 $q$로부터 밀도 도달가능하다고 한다.

Density-reachable

 

Density-connected (밀도 연결)

$p$와 $q$ 모두 어떤 점 $O$로부터 density-reachable하면 $p$는 $q$와 밀도연결되었다고 한다.

Density-connected

Basic Concepts

(하나의) Cluster는 density-connected points의 극대 집합(maximal set)이다.

Border: Cluster에 속하지만 Core는 아니다. (MinPts를 만족하지 못한다.)

Outlier (Noise): 어떠한 클러스터에도 속하지 않는다.

Example for Border, Coer, and Outlier

Example for Border, Core and Noise (Outlier)

DBSCAN Algorithm

1. 임의의 점 $p$를 선택한다.
2. $p$로부터 density-reachable한 모든 점을 모은다.
3. $p$가 core point라면, 클러스터가 형성된다.
4. $p$가 border point라면 모든 점들이 $p$로부터 density-reachable하지 않으므로, 다음 point에 대하여 DBSCAN 알고리즘을 다시 시행한다.
5. 모든 점이 process될 때까지 반복한다.

Pseudo-code for DBSCAN

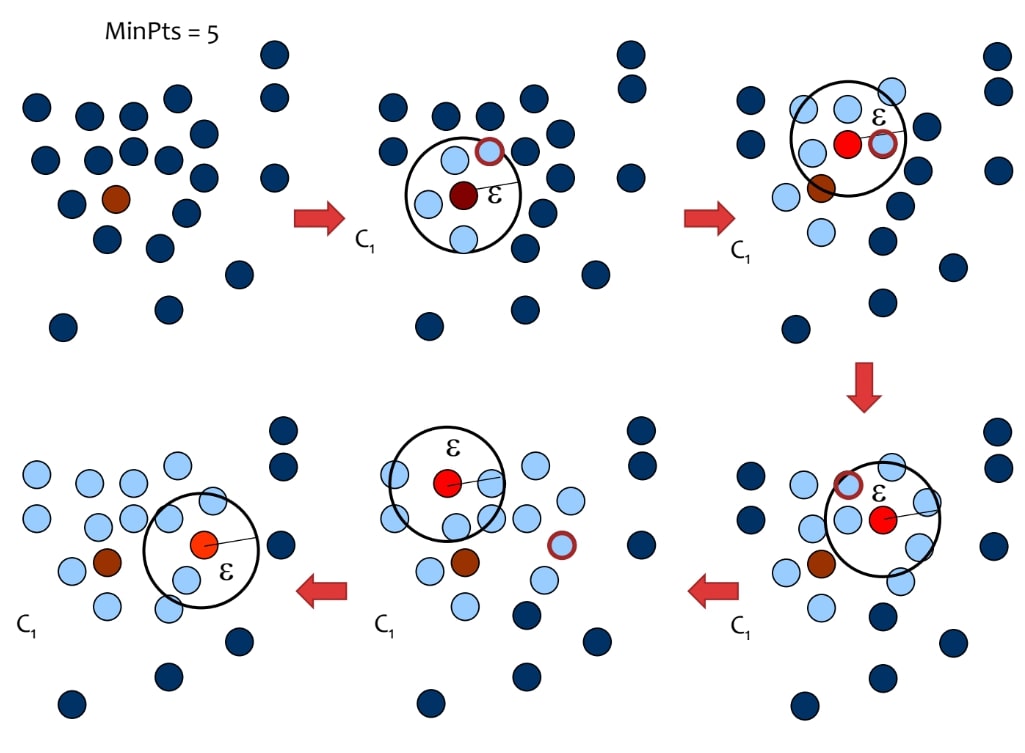
DBSCAN Execution Example

epsilon=2이고 min-points=3으로 미리 파라미터가 세팅되어있고, 분홍색 점들은 아직 classified되지 않은 점들이라 하자.

현재 점($p_1$)을 붉은색이라 하고 이웃반경 $N_{2}(p_1)$를 녹색이라 하자. $\left| N_2(p_1) \right|=3$이므로 $p_1$은 core point이다. density-reachable한 점들을 모으면 녹색이므로 $p_1$은 클러스터 $c_1$으로 분류한다.

$\left| N_2(p_2) \right|=4$이므로 $p_2$은 core point이다. density-reachable한 점들은 녹색이고, $p_2$ 역시 같은 클러스터 $c_1$으로 분류한다.

$\left| N_2(p_3) \right|=5$이므로 $p_3$은 core point이다. density-reachable한 점들은 녹색이고, $p_3$ 역시 같은 클러스터 $c_1$으로 분류한다.

(생략)

unvisited(unclassified) point에서 새로 시작한다. 이 점($p_6$)은  $\left| N_2(p_6) \right|=1$이므로 core point가 아니다. 따라서 NOISE(outlier)로 분류한다.

$\left| N_2(p_7) \right|=3$이므로 $p_7$은 core point이다. density-reachable한 점들은 녹색이고, $p_7$은 새로운 클러스터 $c_2$로 분류한다.

$\left| N_2(p_8) \right|=3$이므로 $p_8$은 core point이다. density-reachable한 점들은 녹색이고, $p_8$은 클러스터 $c_2$로 분류한다.

(생략)

(생략) 마지막 점 역시 $c_2$로 분류한다. 최종적으로 2개의 cluster를 형성했고, 한 점은 outlier로 남아있다.

Example for DBSCAN procedure

반응형

Remarks

Complextity

일반적으로 $O(n^2)$이지만 2차원 데이터에서 index를 사용하면 $O(n \log n)$도 가능하다.

Note: 원 논문에서는 index를 사용하면 $O(n \log n)$이라 주장했으나 후속 논문에 의해 $dim \le 2$ 조건이 필요함이 추가되었다.

Advantages

• cluster 개수를 지정할 필요가 없다. (k-means는 클러스터 개수 $k$를 직접 지정해야 했다.)
• 어떤 모양의 데이터든지 cluster를 형성할 수 있다. (k-means는 구 모양 처럼 convex-shaped만 가능했다.)
• noise를 다룰 수 있다
• data point의 순서에 영향을 받지 않는다. (BIRCH 알고리즘은 순서에 영향을 받는다.)

Disadvantages

• 파라미터(eps, MinPts)의 적절한 값을 찾기 어렵다.
• density가 많이 차이나는 데이터에는 적절하지 않다.

DBSCAN is sensitive to parameters (1)

DBSCAN is sensitive to parameters (2)

 

Determining the Parameters

DBSCAN 논문의 저자들은 heuristic한 방법을 제시했다.

thinnest cluster를 형성하는 parameter를 찾는 아이디어에서 착안했다.

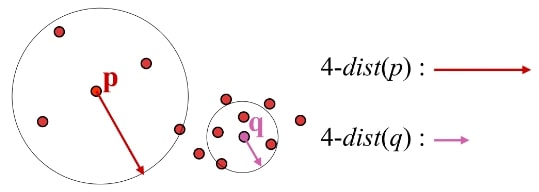
Heuristic method

$k-dist$: 각 점마다 $k$-nearest neighbor를 형성하는 최소 거리

 

MinPts: 고정된 값을 사용한다. 특히 2차원 데이터에 해아여 $4$를 이용할 것을 권장한다.

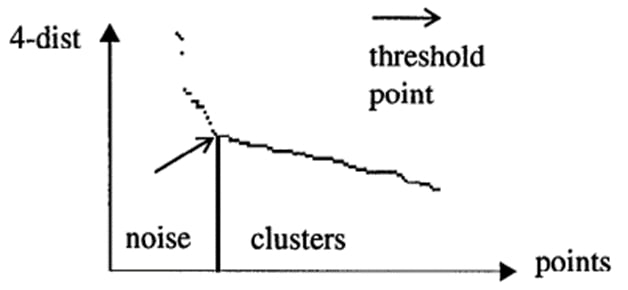
Eps: MinPts-dist 그래프에서 첫번째 꺾인 점(first valley)로 한다.

$4-dist$ for point $p$ and $q$

 

Sorted k-dist graph