Setup
# Start from importing necessary packages.
import warnings
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from IPython.display import display
from sklearn import metrics # for evaluations
from sklearn.datasets import make_blobs, make_circles # for generating experimental data
from sklearn.preprocessing import StandardScaler # for feature scaling
from sklearn.cluster import KMeans
from sklearn.cluster import DBSCAN
# make matplotlib plot inline (Only in Ipython).
warnings.filterwarnings('ignore')
%matplotlib inlineK-means
2차원 공간에서 3개의 구형 클러스터를 만들어보자.
# Generate data.
# `random_state` is the seed used by random number generator for reproducibility (default=None).
X, y = make_blobs(n_samples=5000,
n_features=2,
centers=3,
random_state=170)
# Print data like Ipython's cell output (Only in Ipython, otherwise use `print`).
display(X)
display(y)
'''
array([[-4.01009423, -1.01473496],
[ 1.00550526, 0.13163222],
[ 2.06563121, -0.24527689],
...,
[-5.09493013, 1.47160372],
[-9.61459714, -4.91848716],
[-7.72675795, -5.86656563]])
array([1, 2, 2, ..., 1, 0, 0])
'''
# Plot the data distribution (ground truth) using matplotlib `scatter(axis-x, axis-y, color)`.
plt.scatter(X[:,0], X[:,1], c=y)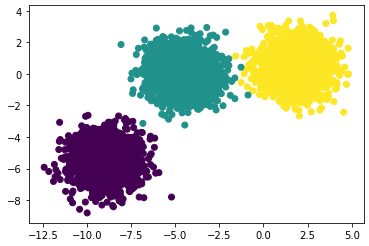
Algorithm
(1) $n$개의 data points $X$에서 랜덤하게 $k$개의 centroid를 뽑는다.
- $X = \{x_1, \dots, x_n \}$
- $C = \{c_1, \dots, c_k \}$
(2) 각 data point $x_i$에 대하여, sum of squared를 distance로 했을 때 가장 가까운 centroid $c_j$를 찾는다.
- $D(x_i, c_j) = \sum_{i=1}^{n} \Vert x_i - c_j \Vert ^2$
(3) 각 cluster마다, cluster에 포함된 데이터들의 평균값을 계산하여 centroid의 좌표를 업데이트한다.
(4) 일정 threshold 이하가 될 때까지(converge) (2)~(3)을 반복한다.
Note: k-means 알고리즘의 exact solution을 찾는 방법은 NP-hard 임이 알려져있다.
# Perform K-means on our data (Train centroids)
kmeans = KMeans(n_clusters=3,
n_init=3,
init='random',
tol=1e-4,
random_state=170,
verbose=True).fit(X)
'''
Initialization complete
Iteration 0, inertia 93044.04597983112.
Iteration 1, inertia 11941.891546455818.
Iteration 2, inertia 9733.27074914065.
Converged at iteration 2: center shift 6.990341405571578e-05 within tolerance 0.0014634111435935595.
Initialization complete
Iteration 0, inertia 49491.22189277588.
Iteration 1, inertia 43229.84746448652.
Iteration 2, inertia 42926.50675387765.
Iteration 3, inertia 42574.50264772275.
Iteration 4, inertia 41999.15634451156.
Iteration 5, inertia 39853.96747003666.
Iteration 6, inertia 28163.261111913765.
Iteration 7, inertia 11338.22462047102.
Iteration 8, inertia 9733.782646928315.
Converged at iteration 8: center shift 0.00037711054168380756 within tolerance 0.0014634111435935595.
Initialization complete
Iteration 0, inertia 35757.30266790044.
Iteration 1, inertia 10003.823957399809.
Iteration 2, inertia 9733.154277459316.
Converged at iteration 2: strict convergence.
'''- n_clusters: 클러스터의 개수. default=8이다. 위 데이터는 3개의 cluster이므로 3으로 세팅했다.
- n_init: k-mean 알고리즘은 초기 centroid에 영향을 받는다. n_init은 centroid 초기화를 몇번 할 것인지에 대한 파라미터이다. 최종 cluster 결과는 best output을 리턴한다. sparse high-dimension인 경우(e.g. document data) n_init을 권장한다.
- init: {k-means++, random, ndarray, callable}이 가능하며 default='k-means++'이다.
- k-means++: converge가 빠른 k개의 centroid로 초기화
- random: 데이터에서 n_cluster 개를 랜덤하게 선택하여 centroid로 초기화
- tol: tolerance. 두 클러스터 center의 거리(Frobenius norm으로 계산)가 tol 이하이면 converge한 것으로 간주한다.
k-mean이 수렴했으니 이제 결과를 살펴보자.
# Retrieve predictions and cluster centers (centroids).
display(kmeans.labels_)
display(kmeans.cluster_centers_)
'''
array([0, 2, 2, ..., 0, 1, 1], dtype=int32)
array([[-4.55676387, 0.04603707],
[-8.94710203, -5.51613184],
[ 1.89450492, 0.5009336 ]])
'''
# Plot the predictions.
plt.scatter(X[:,0], X[:,1], c=kmeans.labels_)
plt.scatter(kmeans.cluster_centers_[:,0],
kmeans.cluster_centers_[:,1],
c='w', marker='x', linewidths=2)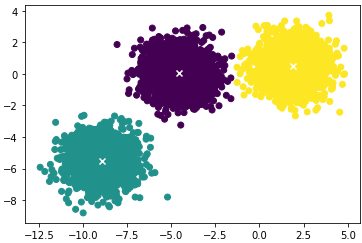
사이킷런의 KMeans() 객체는 재학습 없이 새로운 data point의 cluster label을 예측할 수 있다.
(마치 decition tree의 predict() 메소드와 동일하게 사용할 수 있다.)
# We can make new predictions without re-run kmeans (simpily find nearest centroids).
X_new = np.array([[10,10], [-10, -10], [-5, 10]])
y_pred = kmeans.predict(X_new)
""" The below code is equivalent to:
y_pred = KMeans(...).fit_predict(X), but this needs to fit kmeans again.
"""
display(y_pred) # array([2, 1, 0], dtype=int32)KMeans()의 transform(X) 메소드는 X와 클러스터 center간의 거리를 리턴한다.
# We can get distances from data point to every centroid
""" The below code is equivalent to:
from sklearn.metrics.pairwise import euclidean_distances
euclidean_distances(X_new, kmeans.cluster_centers_)
"""
kmeans.transform(X_new)
'''
array([[17.63464636, 24.48965134, 12.48724601],
[11.42592142, 4.60582976, 15.86659553],
[ 9.96382639, 16.01030799, 11.73739582]])
'''K-means++: A Smarter Way to Initialize Centroids
k-mean 알고리즘의 수렴(속도 및 local minimum에 수렴) centroid 초기값에 매우 의존적이다.
이를 개선한 알고리즘이 사이킷런에 내장되어있고 init='k-means++'로 지정해준다.
(1) $X$에서 uniformly at random하게 $c_1$을 고른다.
(2) next center $c_i = x' \in X$f를 확률 $\cfrac{D(x')^2}{\sum_{x \in X}D(x)^2}$ 내에서 고른다.
(3) $k$개의 center를 고를 때까지 (2)를 반복한다.
(4) k-means 알고리즘을 수행한다.
Paper: k-means++: The Advantages of Careful Seeding
일반적으로 kmeans++이 kmeans보다 빠르게 수렴한다.
# Perform K-means++ on our data.
kmeans_plus_plus = KMeans(n_clusters=3,
n_init=3,
init='k-means++',
tol=1e-4,
random_state=170,
verbose=True).fit(X)
'''
Initialization complete
Iteration 0, inertia 14504.163838606186.
Iteration 1, inertia 9735.744827760547.
Iteration 2, inertia 9733.16763519944.
Converged at iteration 2: center shift 8.017874814669728e-06 within tolerance 0.0014634111435935595.
Initialization complete
Iteration 0, inertia 10751.001848939784.
Iteration 1, inertia 9733.46196513723.
Converged at iteration 1: center shift 0.00012717967226944416 within tolerance 0.0014634111435935595.
Initialization complete
Iteration 0, inertia 12316.398205045829.
Iteration 1, inertia 9733.520322362509.
Converged at iteration 1: center shift 0.00016219913816600037 within tolerance 0.0014634111435935595.
'''# Plot the predictions.
plt.scatter(X[:,0], X[:,1], c=kmeans_plus_plus.labels_)
plt.scatter(kmeans_plus_plus.cluster_centers_[:,0],
kmeans_plus_plus.cluster_centers_[:,1],
c='w', marker='x', linewidths=2)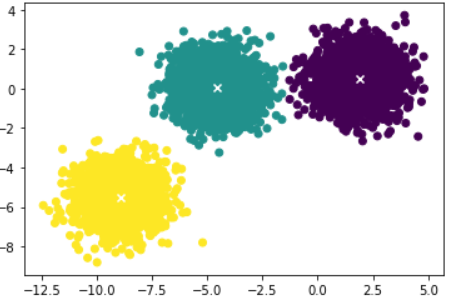
'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| [Clustering] Hierarchical Clustering (계층적 군집화) (0) | 2023.05.22 |
|---|---|
| [Clustering] Drawbacks of K-means and Solutions with Python (K-means 단점과 해결방법) (0) | 2023.05.21 |
| [Clustering] Model-based Methods, Expectation Maximization (EM) (0) | 2023.05.19 |
| [Clustering] Partitioning Methods, K-Means Clustering, PAM, k-Medoids Clustering (0) | 2023.05.18 |
| [Clustering] Overview, Approach, Cluster Analysis (0) | 2023.05.17 |



