[Data Science] Decision Tree - Model Evaluation (Confusion Matrix, Metric, ROC Curve, AUC Score)

반응형

Confusion Matrix

How to interpret Confusion Matrix

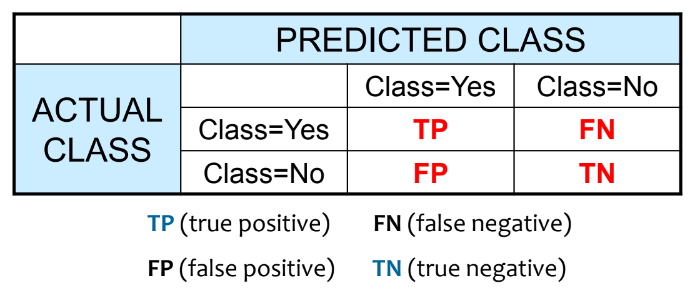
Classification에 대하여 confusion matrix(혼동행렬)을 이용하여 결과를 볼 수 있다.

Positive와 Negative는 각 클래스 이름이다.(이진 분류에서 P와 N을 주로 사용한다)

각 분류에 대하여 True는 actual와 predicted가 일치하는 것을, False는 actual와 predicted가 불일치하는 것을 나타낸다.

 

 

(분류기) 모델의 정확도(Accuracy)는 Positive와 Negative를 얼마나 정확하게 분류한지에 대한 평가지표이다.

\[ \text{Accuracy} = \cfrac{TP + TN}{TP + TN + FP + FN} \]

 

Class Imbalance Problem

accuracy는 imbalanced class에서 모델의 성능평가를 왜곡할 수 있다.

예를 들어 어떤 질병에 대한 분류기를 평가해보자.

그런데 이 질병은 매우 희귀해서 10,000개 데이터 중에서 10개만 양성(Positive)이고 나머지는 음성(Negative)이다.

만일 이진분류기기가 (잘못 학습해서) 모든 데이터에 대하여 무조건 음성판정만 내린다고 하자. 분명히 잘못된 결과이지만 accuracy는 99.9%(=9990/10000)로 매우 정확하다.

 

이 원인은 애초에 데이터 클래스가 불균형하기 때문이다. 따라서 새로운 평가지표가 필요하다.

 

Sensitivity (True Positive Rate, 민감도)

\[ TPR = \cfrac{TP}{P} = \cfrac{TP}{TP + FN} \]

 

Specificity (True Negative Rate 특이도)

\[ SPC = \cfrac{TN}{N} = \cfrac{TN}{FP + TN} \]

 

Classifier Evaluation Metrics

precision, recall, f1-score가 자주 사용된다.

 

Precision(exactness, 정밀도)

분류기가 P로 분류한 튜플들(TP, FP)이 TP일 확률

\[ precision = \cfrac{TP}{TP + FP} \]

 

Recall(completeness 재현율)

실제(Actual) P 중에서(TP, FN) 모델이 P로 분류할 확률

\[ recall = \cfrac{TP}{TP + FN} \]

 

F-measure(F1, F-score)

precision과 recall의 조화평균

\[ F_1 = \cfrac{2}{\cfrac{1}{precision} + \cfrac{1}{recall} } = 2 \times \cfrac{precision \times recall}{precision + recall} \]

 

Example

Example Confusion Matrix

precision = 90/(90+140)=90/230=39.13%

recall = 90/(90+210) = 90/300=30.00%

 

Accuracy가 96.50%으로 굉장히 높아보이지만 sensitivity는 30%로 TPR은 처참하다.

 

Remind

$\text{sensitivity} (TPR) = TP / T_{actual}$

$\text{specificity} (TNR) = TN / N_{actual}$

$\text{precision} = TP / T_{pred}$

$\text{recall} = TP / T_{actual}$

ROC Curve (Reciever Operating Characteristic Curves)

Binary Classifier Cyctem에서 threshold의 변화에 따라 분류기의 성능을 시각화 한 그래프이다.

Diagnostic test 끼리 평가하기 위한 방법이다.

An example of ROC curve

Underlying Theory

질병에 대하여 양성/음성반응이 정확히 분리되지 않을 것이다. 실제로는 두 분포가 겹치는 구간이 존재할 것이다.

가능한 모든 cut-off point(criterion value)마다 우리는 두 클래스를 구별한다고 하자.

실제 질병인 집단에서, 양성으로 판단될 수 있지만(TP) 양성인데 음성인 경우(FN)인 경우도 있을 것이다.

반대로, 질병이 아닌 집단에서도 진짜로 음성(TN)일 수 있지만, 양성인 경우(FP)인 경우도 있을 것이다. 

(코로나 진단 키트를 생각해보자)

Disease Distribution

Positive cases의 분포를 $f_P$, Negative의 분포를 $f_N$, threshold parameter를 $T$라 하면

$\displaystyle TPR(T) = \int_T^{\infty} f_P(x)\ dx$ (TP + FN이 $f_P$에 속하기 때문)

$\displaystyle FPR(T) = \int_T^{\infty} f_N(x)\ dx$ (TN + FP가 $f_N$에 속하기 때문)

 

(분포는 그대로 두고) cut-off point(criterion value) 값이 변화함에 따라 TP, FP, TN, FN에 대한 비율이 달라진다.

 

ROC Space and Point

위에 언급한 sensitivity와 specifity를 이용하여 곡선을 그린 것이다.

x축) 1-specificity는 false positive rate (FPR) $FPR = 1 - \cfrac{TN}{TN + FP} = \cfrac{FP}{TN + FP} = \cfrac{FP}{N_{actual}}$

y축) sensitivity로 true positive rate (TPF) $TPF = \cfrac{TP}{TP + FN} = \cfrac{TP}{T_{actual}}$

 

아래 4개 confusion matrix에 대하여 ROC Space에 점을 표시해보자. (TPR와 FPR를 계산하는 건 생략)

Examples of 4 points

ROC Space from A, B, C, C'

 

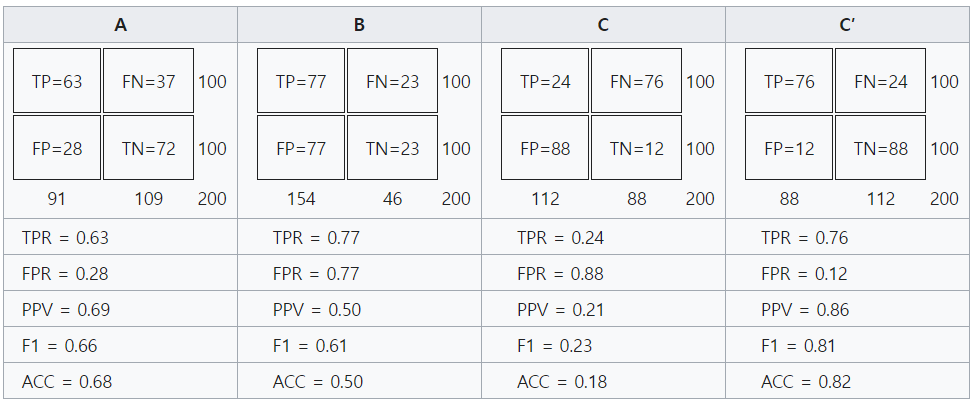
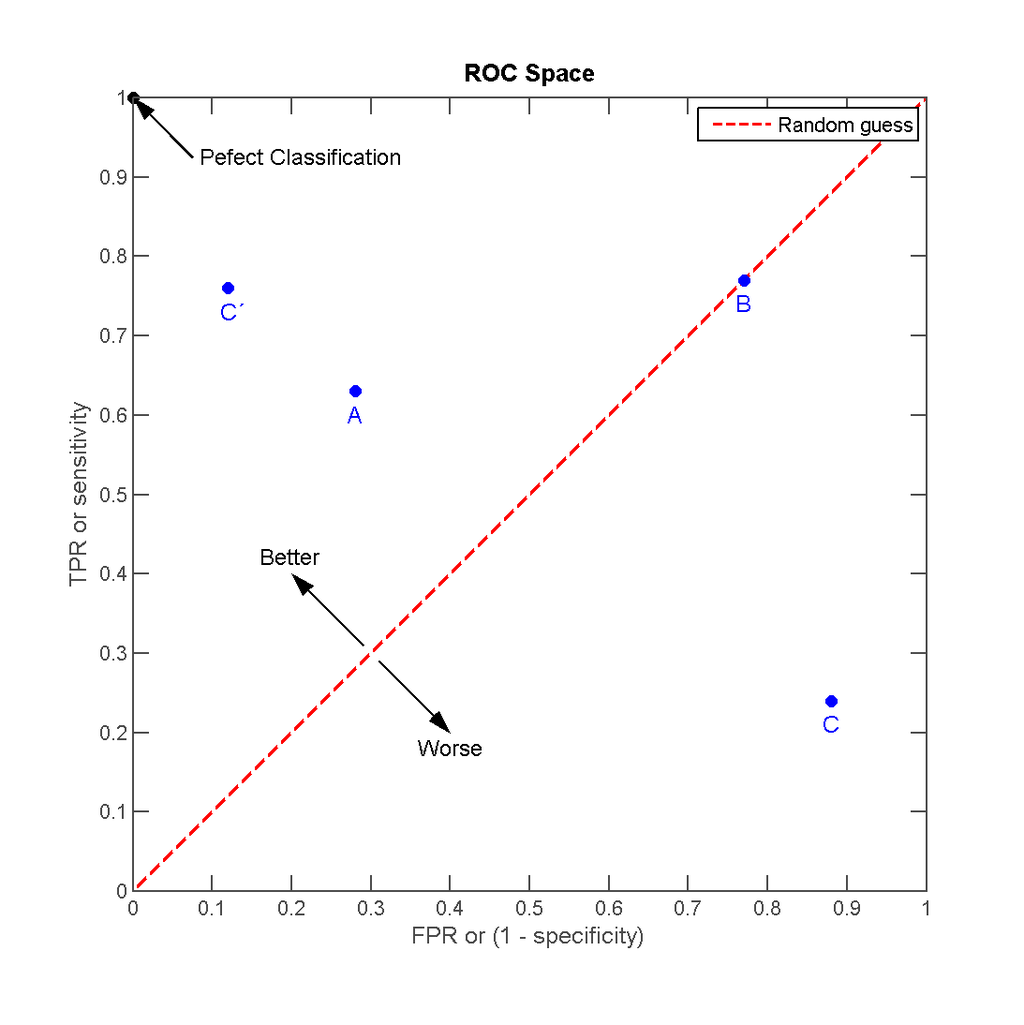
Construction of a ROC Curve

- ROC Point의 (x, y)는 각각 (1-specificity, sensitivity)를 의미한다.

- ROC curve는 모든 ROC point를 ROC space에 나타낸 것이다.

- 이웃한 두 ROC point는 직선으로 연결한다.

- ROC curve의 시작은 (0, 0)이고 끝은 (1, 1)이다.

 

아래 예시 데이터를 이용하여 ROC curve를 그려보자.

Class 밑의 row는 어떤 parameter라고 생각하고, 이 값이 변하면서 classifier의 결과가 달라질 것이다.

Example Confusion Matrix

ROC Curve

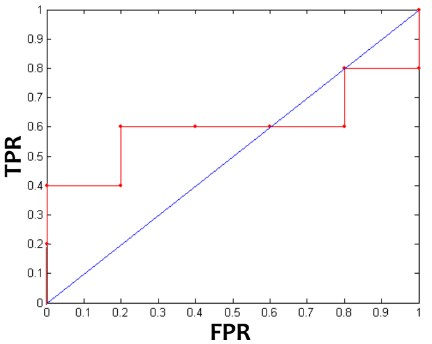
※ 데이터 수가 적어서 curve가 아니라 꺾인 선으로만 보인다. 

 

Interpreting ROC Curve

이제 ROC curve를 그렸으니 그래프를 해석해보자.

 

 

 

 

Random Classifier

만일 classifier가 두 class를 구별하지 못한다고 하자. (random guessing, random performance)

이 경우 threshold의 값과 상관없이 항상 $TP=FP$ and $TN=FN$이므로 $TPR=FPR$이다.

($\cfrac{TP}{TP+FN} = \cfrac{FP}{TN+FP}$)

Random Classifier

그렇다면 ROC curve는 $y=x$ 직선과 동일하게 그려진다.

ROC Curve of Random Classifier

 

Perfect Classifier

만일 classifier가 정확하게 두 class를 분류한다고 하자. (perfect performance)

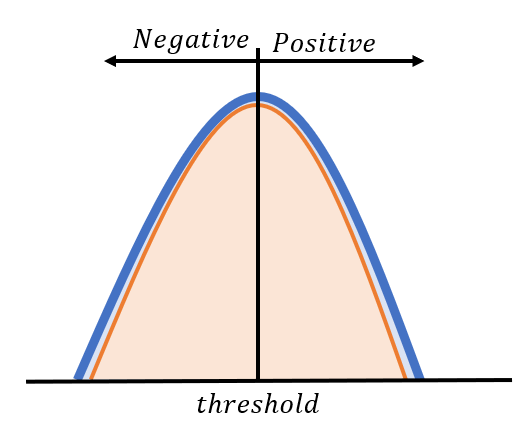
아래와 같이 좌측에 Negative distribution이, 우측이 Positive distribution이 분포한다고 하자.

Perfect Classifier

threshold가 Negative distribution에 있다고 하자.

Positive) $TP$만 존재한다. 따라서 $TPR=1$

Negative) $TN$은 증가하고 $FP$는 감소한다.($TN+FP$는 일정) 따라서 $FPR$는 증가한다.

종합하면 $TRP=1$일 때 $FPR$은 $[0, 1]$내에서 모든 값이 가능하다.

 

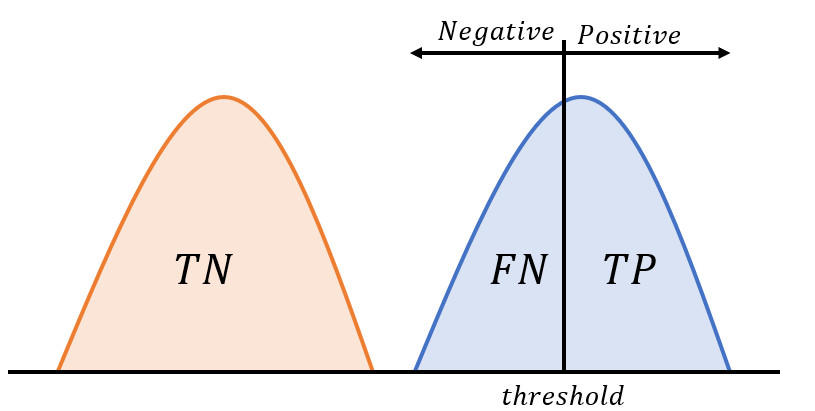
threshold가 Positive distribution에 있다고 하자.

Positive) $TP$는 감소하고 $FN$는 증가한다. 따라서 $TPR$는 감소한다.

Negative) TN만 존재한다. 따라서 $FPR=0$이다.

종합하면 $FPR=0$일 때 $TPR$은 $[0, 1]$내에서 모든 경우가 가능하다.

 

이를 ROC curve로 나타내면 다음과 같다.

ROC Curve of Perfect Classifier

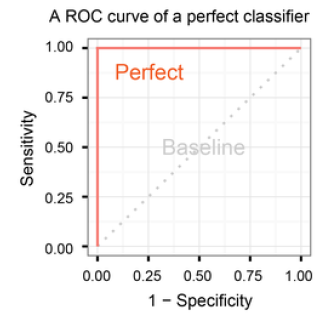
이를 종합하여 일반적으로 설명해보자.

classifier가 random classifier라면 ROC curve는 $y=x$ 이다.

그리고 classifier의 성능이 좋다면 (두 class의 distribution을 잘 분류한다면) ROC curve는 $(0, 1)$에 가까운 위로 오목한 곡선을 그릴 것이다.

만약 $y=x$ 밑으로 곡선이 그려진다면, class를 반대로 분류한다고 생각하면 된다. (random classifier보다 나쁜 성능을 갖는다)

 

같은 Classifier에 대하여 distribution은 변하지 않으므로 하나의 classifier는 하나의 ROC curve를 그린다.

하나의 ROC curve는 Classifier의 성능은 그대로인 채(distribution 그대로) 모든 threshold에 대하여 $TPR$과 $FPR$를 모두 그린 것이다.

The ROC space for a "better" and "worse" classifier.

Comparison of Multiple Models

위에서 살펴보았듯이, ROC curve가 perfect인 경우와 가장 가까운 곡선이 성능이 좋다.

따라서 두개 이상의 classifier는 같은 수의 ROC curve를 그리는데, 가장 좌상단으로 찌그러진(?) 모델의 성능이 좋다고 해석할 수 있다.

 

아래 그림의 경우 파란선의 $A$의 성능이 $B$보다 좋다는 것을 알 수 있다.

Classifier A clearly outperforms Classifier B

 

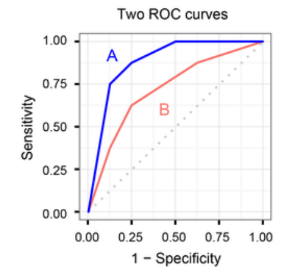
AUC Score (Area Under the ROC Curve)

ROC space에서 ROC curve 밑의 넓이를 의미한다.

위의 경우처럼 $A$가 항상 $B$의 위에 있다면 $A$의 성능이 더 좋다고 할 수 있다.

그러나 많은 경우에 ROC curve는 서로 교차하면서 겹치게 된다.

 

수치적으로 성능을 비교하기 위한 방법 중 하나로 AUC를 이용할 수 있다.

예를 들어 random classifier의 경우 $AUC=0.5$이고 perfect classifier의 경우 $$AUC=1.0$이다.

AUC 면적(범위: $[0, 1]$)이 넓을 수록 분류기의 성능이 좋다.

AUC Scores

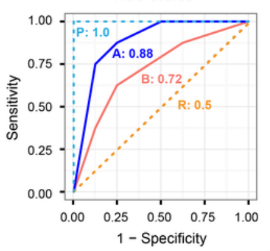
항상 AUC score를 이용하지는 않는다. 예를 들어 의료 도메인의 경우 오탐(질병을 놓치는 것)을 낮추는 것이 더 중요할 수 있다. 이 경우에는 AUC가 다소 낮더라도 TPR이 높은 모델을 선택할 수 있다.