Entropy
이전 포스팅에서 엔트로피에 대해 간단히 다뤄보았다.
이제 엔트로피를 이용한 정보획득(information gain, IG)을 이용한 decision tree를 살펴보자.
https://trivia-starage.tistory.com/106?category=1047124
Entropy의 의미 (정보이론)
Entropy in information theory 정의 정보이론에서, 확률변수의 엔트로피는 변수의 불확실성의 기댓값이다. $\mathcal{X}$에서 추출한 (이산)확률변수 $X$의 엔트로피를 $H(X)$라 하고 아래와 같다. \[ H(X) = -\sum
trivia-starage.tistory.com
\[ Entropy = -\sum_{i}p_i \log_2{p_i} \]
Note: 이번 포스팅에서 특별한 언급이 없는 한 로그의 밑은 $2$로 간주한다.
$C$개의 class에 대하여, 엔트로피가 최대인 경우는 모든 record가 모든 클래스에 균일하게 분포한 경우이다. 따라서 각 클래스 별로 확률은 $1/C$이므로
$Entropy = -\sum_{i=1}^{C}\frac{1}{C}\log{\frac{1}{C}} = \log{C}$
엔트로피가 최소인 경우는 모든 record가 오직 하나의 클래스만 가진 경우이다. 이 경우 해당 클래스의 확률은 $1$이고 나머지 확률은 $0$이므로 $Entropy = 0$이다.
Examples for Computing Entropy
$\{C_1:0,\ C_2:6 \}$일 때, $p_1=0,\ p_2=1$이므로
$Entropy = -(0\cdot \log0 + 1\cdot \log1) = 0$ 이다.
$\{C_1:1,\ C_2:5 \}$일 때, $p_1=1/6,\ p_2=5/6$이므로
$Entropy = -((1/6)\cdot \log(1/6) + (5/6)\cdot \log(5/6)) = 0.65$ 이다.
$\{C_1:2,\ C_2:4 \}$일 때, $p_1=2/6,\ p_2=4/6$이므로
$Entropy = -((2/6)\cdot \log(2/6) + (4/6)\cdot \log(4/6) = 0.92$ 이다.
Information Gain
Parent node $p$가 $k$개의 partition으로 나뉜다고 하고, 각 $i$번째 partition에는 $n_i$개의 record가 있다고 하자.
\[ Gain = Entropy_{\text{Before Split}} - Entropy_{\text{After Split}} \]
$Entropy_{\text{Before Split}} = Entropy(p)$
$Entropy_{\text{After Split}} = \sum_{i=1}^{k}\cfrac{n_i}{n}Entropy(i)$
Information Gain이 가장 큰 (Entropy가 가장 많이 감소하는 = 가장 pure하게 만드는) 방향으로 split한다.
Information Gain은 ID3 알고리즘에서 사용된다.
단점: partition을 가장 많이 split하는 쪽을 선호하는 경향이 생긴다. (partition이 많을 수록 더 pure할 것이기 때문)
예시) Student_ID와 같은 변수는 각 partition마다 한 개의 record만 가지게 된다.
Example
14개의 record가 있고 4개의 기상 정보 feature(Outlook, Temperature, Humidity, Wind)와 binary target (Play Tennis)로 구성되어있다. 각 날짜별로 주어진 기상 정보가 주어졌을 때, play tennis를 할 것인지 분류하는 decision tree를 만들어보자.

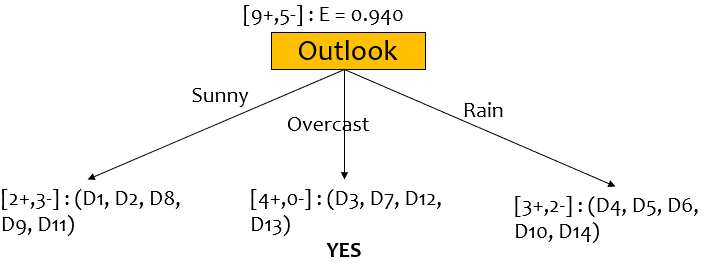
Before Split, $D$
초기 단계 $D$의 엔트로피를 구하자. yes(+)와 no(-)가 각각 9개, 5개 있으므로
$Entropy(D) = -((9/14)\log(9/14) + (5/14)\log(5/14)) = 0.940$
Wind
Wind에 대하여 엔트로피를 구하고, IG를 계산해보자.
Wind는 2개의 attribute (Weak, Strong)이 존재한다. 각각 class의 분포를 살펴보면 $D_{weak}=[6+, 2-],\ D_{strong}=[3+, 3-]$이고 각각의 엔트로피는
$Entropy(D_{weak}) = -((6/8)\log(6/8) + (2/8)\log(2/8)) = 0.811$
$Entropy(D_{strong}) = -((3/6)\log(6/8) + (3/6)\log(2/8)) = 1.00$
따라서 Wind에 의한 IG는
\begin{align*} IG(D, Wind) &= Entropy(D) - \sum_{v \in \{weak,\ strong\} }\cfrac{|D_v|}{|D|}Entropy(D_v) \\ &= Entropy(D) - \cfrac{8}{14}Entropy(D_{weak}) - \cfrac{6}{14}Entropy(D_{strong}) \\ &= 0.940 - \cfrac{8}{14}(0.811) - \cfrac{6}{14}(1.00) \\ &= 0.048 \end{align*}
Humidity
Humidity는 2개의 attribute를 갖고 클래스별 분포는 $D_{high}=[3+, 4-],\ D_{normal}=[6+, 1-]$ 이다.
따라서 엔트로피를 계산하면 (식 생략) $Entropy(D_{high}) = 0.985,\ Entropy_{D_{normal}} = 0.592$
따라서 IG를 계산하면
$IG(D, Humidity) = 0.940 - \frac{7}{14}(0.985) - \frac{7}{14}(0.592) = 0.151$
Outlook
Outlook은 3개의 attribute가 있고 각 분포를 살펴보면 $D_{sunny}=[2+, 3-],\ D_{overcast}=[4+, 0-],\ D_{rain}=[3+, 2-]$이다.
엔트로피를 계산하면
$Entropy(D_{sunny}) = 0.971$, $Entropy(D_{overcast}) = 0.0$, $Entropy(D_{rain}) = 0.971$ 이다.
따라서 IG를 계산하면
$IG(D, Outlook) = 0.940 - (5/14)(0.971) - (4/14)(0.0) - (5/14)(0.971) = 0.246$
Best split
$IG(D, Outlook) = 0.246$, $IG(D, Temperature) = 0.029$, $IG(D, Humidity) = 0.151$, $IG(D, Wind) = 0.048$이고 이중 가장 information gain이 많은건 Outlook이다.
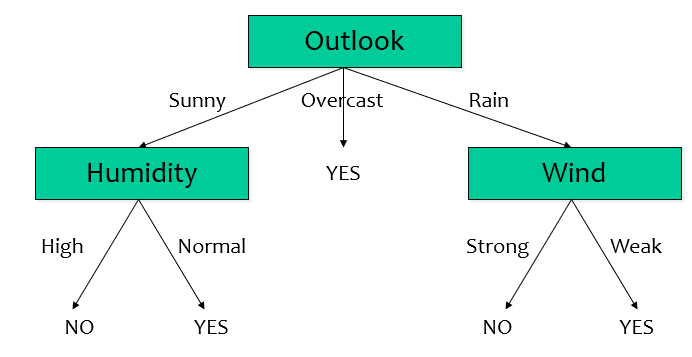
따라서 Outlook 대로 split하고 record를 재분배한다.
Outlook=Overcast 인 node의 경우, 모든 record가 yes이므로 더이상 split하지 않는다.
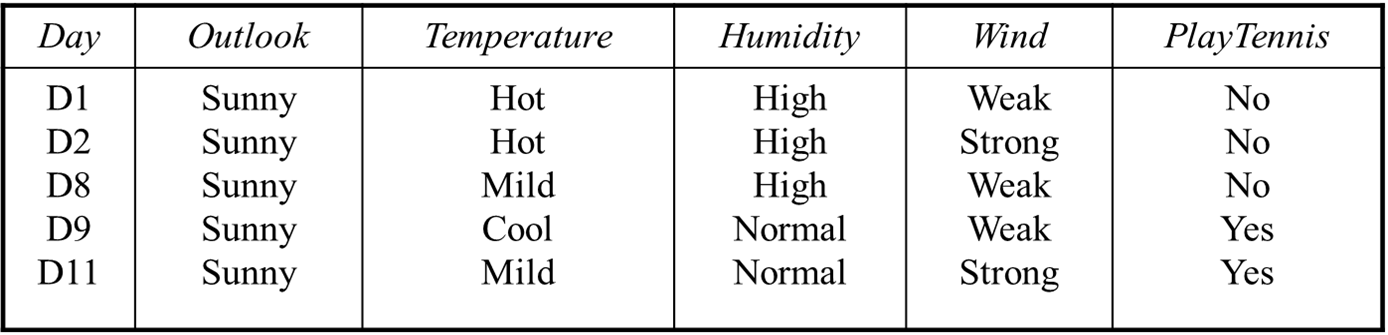
$D_{sunny}$
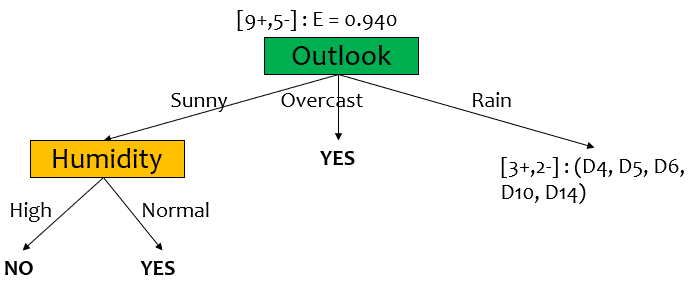
왼쪽으로 분기된 Sunny에 대하여 재귀적으로 information gain을 구해보자.
이제 sunny는 before split node이므로 전체 엔트로피를 구하면
$Entropy(D_{sunny}) = -(2/5)\log(2/5) -(3/5)\log(3/5) = 0.971$
Temperature: $D_{hot}=[0+, 2-], D_{mild}=[1+, 1-], D_{cool}=[1+, 0-]$이고 $IG(D_{sunny}, Temperature)=0.571$
Wind: $D_{weak}=[1+, 2-], D_{string}=[1+, 1-]$.
$Entropy(D_{weak})=0.918$, $Entropy(D_{string})=1.0$
$IG(D_{sunny}, Wind) = 0.020$
Humidity: $D_{high}=[0+, 3-], D_{normal}=[2+, 0-]$
$Entropy(D_{high}) = 0.00$, $Entropy(D_{normal}) = 0.00$
$IG(D_{sunny}, Humidity) = 0.971$
IG가 가장 큰 것은 Humidity이므로 이쪽으로 split한다.
Humidity로 split 된 node들은 모두 pure하므로 NO/YES로 leaf node로 만든다.
$D_{rain}$
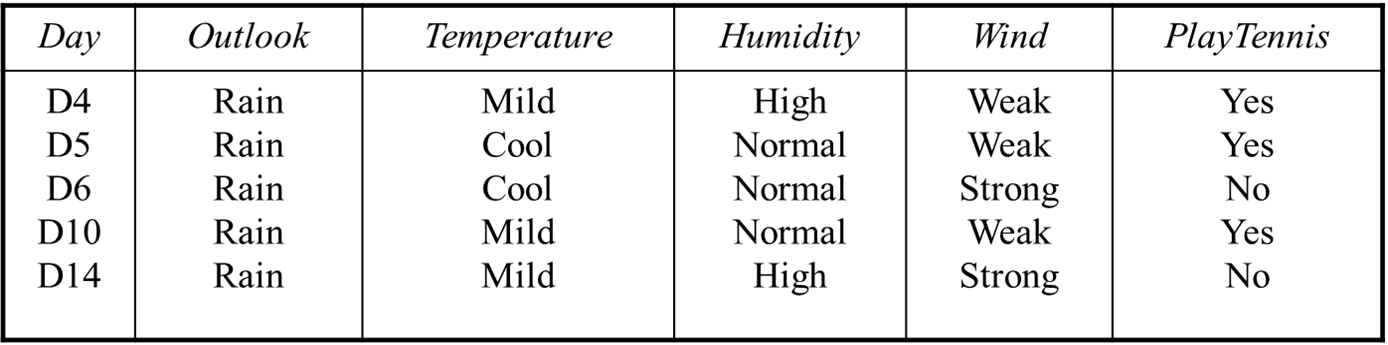
앞에서와 같이 각 feature마다 엔트로피와 gain을 계산하면 된다.
(마음의 눈으로 바라보면) Wind의 경우 purely split할 수 있다는 것을 알 수 있다. (weak는 yes로, strong은 no로)
따라서 IG가 가장 큰 것은 Wind이다.
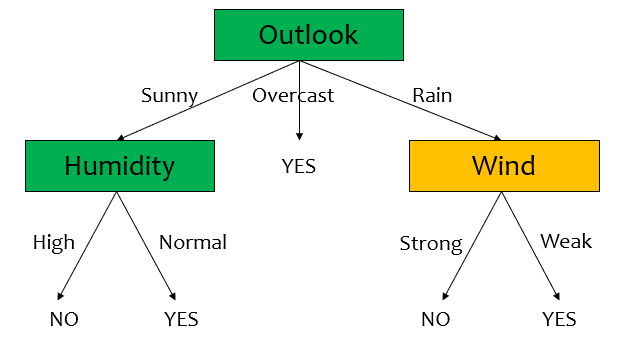
Drawback of the Information Gain
앞에서 살짝 언급했지만, information gain의 단점 역시 존재한다. 어떤 attribute가 굉장히 많은 구별되는 값(a large number of distinct values)을 가지는 경우 information gain이 높아지는 경향이 있기 때문이다.
예를 들어, Student_ID, CreditCardNumbers와 같은 attribute를 생각해보자. 각 student 혹은 customer를 unique하게 식별할 수 있다. 그렇기 때문에 Entropy는 매우 낮을 것이고 Information Gain 역시 매우 커서 split하려고 할 것이다.
그러나 이는 overfitting 문제가 있다. 왜냐면 우리가 보지 않은 데이터에 대해서 제대로 일반화하지 못할 것이기 때문이다.
위의 테니스 데이터셋에서 Day에 대하여 살펴보자. 각 Day1, ..., Day14는 unique하기 때문에 target value(Play Tennis)를 정확히 식별한다. 따라서 각 Entropy는 $0$이 되고 $IG(D, Day)=0.940-0=0.940$으로 위에서 계산한 Outlook의 경우보다 크다. 그러나 다른 날짜(예를 들어 Day20)가 포함된 데이터에서는 제대로 동작하지 않을 것이다.
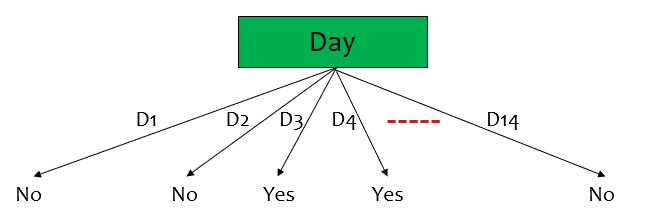
Gain Ratio (Information Gain Ratio, IGR)
Parent node $p$가 $k$개의 partition으로 나뉘어지고, 각 $i$번째 partition의 크기를 $n_i$라 할 때
\[ GainRatio = \cfrac{IG}{SplitInformation}, \qquad SplitInformation = -\sum_{i=1}^{k}\cfrac{n_i}{n}\log{\cfrac{n_i}{n}} \]
$SplitInformation$이 클 수록 Importance는 줄어든다.
Gain Ratio는 C4.5 알고리즘에 사용된다.
Gain Ratio Example
위 테니스 데이터에서 Day에 대한 Gain Ratio를 구해보자.
$SplitInfo([1, 1, \dots, 1]) = 14 \cdot (-\frac{1}{14}\log{\frac{1}{14}})=3.807$
따라서 $GainRatio(Day)=\frac{0.940}{3.807}=0.246$ ($IG$는 위에서 구한 $0.940$을 이용함)
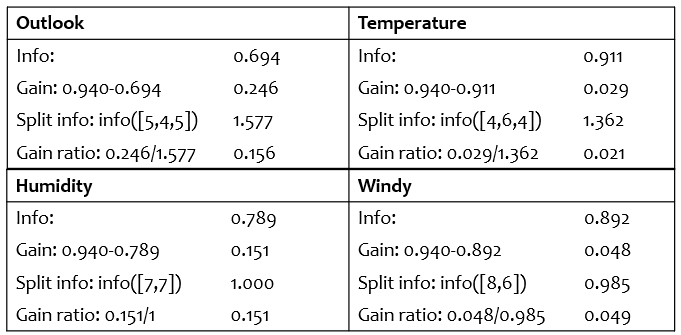
4개의 변수들의 Gain Ratio를 계산하면 Outlook이 여전히 가장 높은 값을 가진다.
그러나, Gain Ratio의 관점에서도 $IGR(Day) > IGR(Outlook)$ 인 문제가 있다.
일반적으로 이를 해결하기 위해서, standard fix를 한다.
standard fix란, ad hoc test를 통해 애초에 unique한 attribute를 제외하고 decision tree를 만드는 것이다.
Drawback of the Gain Ratio
Gain Ratio는 overcompensate하는 문제가 있다.
split-info가 Gain Ratio와 반비례하기 때문에, 단순히 split-info가 작은 attribute를 선택할 가능성이 존재한다.
'스터디 > 데이터사이언스' 카테고리의 다른 글
| [Data Science] Decision Tree - Model Evaluation (Confusion Matrix, Metric, ROC Curve, AUC Score) (0) | 2023.04.30 |
|---|---|
| [Data Science] Decision Tree - Overfitting (0) | 2023.04.29 |
| [Data Science] Decision Tree in R (0) | 2023.04.28 |
| [Data Science] Missing Values (0) | 2023.04.21 |
| [Data Science] Chi-square test. 카이제곱검정 (0) | 2023.04.20 |



