
지금까지 공부한 내용은 그래프, GNN, Node embedding이다.
이렇게 얻은 결과는 node embedding 집합이다. $\{ \mathbf{h}_v^{(L)}, v \in G \}$
이제 GNN으로 Prediction Task를 할 것이다.
크게 3가지 prediction이 있고 node-level, edge-level, graph-level prediction으로 나눌 수 있다.
Node-level prediction
node-level prediction의 경우, 노드 임베딩을 직접 이용할 수 있다.
$L$개의 layer를 가진 GNN을 통과하여 $d$차원 노드임베딩을 얻을 수 있다,
\[ \{ \mathbf{h}_v^{(L)} \in \mathbb{R}^d, \forall v \in G \} \]
$k$-way prediction을 고려하자. 분류와 회귀의 경우 아래와 같다.
- Classification: $k$개의 category 분류
- Regression: $k$개의 target 예측(회귀)
노드 임베딩을 이용하여 예측한 노드를 $\hat{\mathbf{y}}_v$이라 하면 다음과 같은 수식으로 표현한다.
\[ \hat{\mathbf{y}}_v = \text{Head}_{\text{node}}(\mathbf{h}_v^{(L)}) = \mathbf{W}^{(H)} \mathbf{h}_v^{(L)} \]
- $\hat{\mathbf{y}}_v \in \mathbb{R}^k$: $k$-way target
- $\mathbf{h}_v^{(L)} \in \mathbb{R}^d$
- $\mathbf{W}^{(H)} \in \mathbb{R}^{k \times d}$: $d$차원 노드임베딩을 $k$차원 label에 매핑하는 행렬
Edge-level prediction

노드 임베딩의 쌍으로 edge를 예측한다.
\[ \hat{\mathbf{y}}_{uv} = \text{Head}_{\text{edge}}(\mathbf{h}_u^{(L)},\ \mathbf{h}_v^{(L)}) \]
그렇다면 어떻게 $\text{Head}_{\text{edge}}(\mathbf{h}_u^{(L)},\ \mathbf{h}_v^{(L)})$를 정의할 것인가?
(1) Concat + Linear

\[ \hat{\mathbf{y}}_{uv} = \text{Linear}(\text{Concat}(\mathbf{h}_u^{(L)}, \mathbf{h}_v^{(L)}) ) \]
$\text{Linear}(\cdot)$는 $2d$ 차원을 $k$ 차원으로 매핑한다. (concat을 해서 길이가 $2d$차원이다)
(2) Dot prouct
\[ \hat{\mathbf{y}}_{uv} = (\mathbf{h}_u^{(L)})^\top \mathbf{h}_v^{(L)} \]
이 방법은 오직 1-way prediction에만 적용할 수 있다. (ㄷe.g., link prediction: edge의 존재성 예측)
$k$-way prediction으로 확장하려면 multi-head attention처럼 $k$개의 weight를 학습한다. ($\mathbf{W}^{(1)}, \cdots, \mathbf{W}^{(k)}$)
\[ \hat{\mathbf{y}}_{uv}^{(1)} = (\mathbf{h}_u^{(L)})^\top \mathbf{W}^{(1)} \mathbf{h}_v^{(L)} \]
\[ \cdots \]
\[ \hat{\mathbf{y}}_{uv}^{(1)} =(\mathbf{h}_u^{(L)})^\top \mathbf{W}^{(k)} \mathbf{h}_v^{(L)} \]
\[ \hat{\mathbf{y}}_{uv} = \text{Concat}(\hat{\mathbf{y}}_{uv}^{(1)}, \cdots, \hat{\mathbf{y}}_{uv}^{(k)}) \in \mathbb{R}^k\]
Graph-level prediction

\[ \hat{\mathbf{y}}_G = \text{Head}_{\text{graph}}(\{ \mathbf{h}_v^{(L)} \in \mathbb{R}^d, \forall v \in G \}) \]
(1) Global Pooling
Global mean pooling: $\hat{\mathbf{y}}_{G} = \text{Mean}(\{ \mathbf{h}_v^{(L)} \in \mathbb{R}^d, \forall v \in G \})$
Global max pooling: $\hat{\mathbf{y}}_{G} = \text{Max}(\{ \mathbf{h}_v^{(L)} \in \mathbb{R}^d, \forall v \in G \})$
Global sum pooling: $\hat{\mathbf{y}}_{G} = \text{Sum}(\{ \mathbf{h}_v^{(L)} \in \mathbb{R}^d, \forall v \in G \})$
이러한 pooling은 small graph에는 잘 동작하지만 large graph의 경우 잃어버리는 정보가 생긴다.
Issue of Global Pooling
예를 들어 5개의 1차원 노드 임베딩을 가진 그래프에 global pooling을 해보자.
$G_1 = \{ -2, -1, 0, 1, 2 \}$
$G_2 = \{ -20, -10, 0, 10, 20 \}$
이 두 그래프는 노드임베딩이 다르므로 다른 구조(그래프)를 가질 것이다.
그러나 global sum pooling을 하면
$\hat{\mathbf{y}}_{G_1} = \text{Sum}(\{ -2, -1, 0, 1, 2 \}) = 0$
$\hat{\mathbf{y}}_{G_2} = \text{Sum}(\{ -20, -10, 0, 10, 20 \}) = 0$
sum pooling을 통과한 두 그래프의 값이 같기 때문에 (분명히 다르지만) 두 그래프를 구별할 수 없다.
(2) Hierarchical Global Pooling
노드 임베딩을 계층적으로 aggregate하여 global pooling의 문제를 해결할 수 있다.
예를 들어 $\text{ReLU(Sum)}$을 적용해보자.
계층을 간단히 하기 위해 노드임베딩을 2개와 3개로 나누어서 계산해보자.
$\text{ReLU}(\text{Sum}(\{-2,\ -1 \}))=0,\ \text{ReLU}(\text{Sum}(\{ 0,\ 1,\ 2 \}))=3$이므로 $\hat{\mathbf{y}}_{G_1}=3$
$\text{ReLU}(\text{Sum}(\{-20,\ -10 \}))=0,\ \text{ReLU}(\text{Sum}(\{ 0,\ 10,\ 20 \}))=30$이므로$\hat{\mathbf{y}}_{G_2}=30$
따라서 $G_1$과 $G_2$를 구별할 수 있다.
DiffPool
각 level 별로 독립된 GNN을 구성한다. 그리고 GNN-A와 GNN-B는 병렬적으로 실행할 수 있다.
GNN-A: node embedding
GNN-B: 노드가 어디에 속하는지 clustering
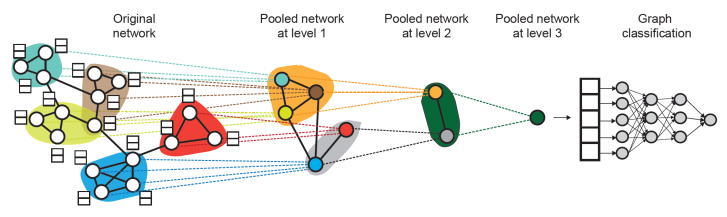
GNN-B를 이용하여 clustering을 하고, 각 클러스터에 속한 노드들로 GNN-A를 통해 node embedding을 한다.
각 cluster마다 새로운 한 개의 노드를 만들고(위 그림에서 같은 색으로 매핑된 노드), 그렇게 pooled node끼리 연결하여 새로운 그래프(pooled network)를 만든다.
'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| [Machine Learning] SVM in Python (1) Decision Boundary (0) | 2023.05.10 |
|---|---|
| [Machine Learning] SVM (Support Vector Machine) (0) | 2023.05.09 |
| [CS224w] Graph Augmentation (0) | 2023.04.24 |
| GAT, GraphSAGE (0) | 2023.04.19 |
| [GCN] Graph Convolutional Network (0) | 2023.04.18 |



