Synopsis
sklearn의 iris dataset으로 간단히 binary classification을 해보자.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn import datasets
from sklearn.metrics import confusion_matrix
SVC의 defalut kernel은 'rbf'이지만 linear로 먼저 살펴보자
# Load Iris dataset
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = iris["target"]
# setosa 와 versicolor 를 분류하는 데이터만 선택
setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]
# build SVM-Classifier and fit
svm_clf = SVC(kernel="linear", C=1e6) # Constraint 강하게
svm_clf.fit(X, y)
# predict
y_pred = svm_clf.predict(X)
confusion_matrix(y, y_pred)
'''
array([[50, 0],
[ 0, 50]])
'''confusion matrix를 보아, 모두 TF, TN으로 분류하였다.
Visualization
kernel이 linear이고, 사용한 feature가 2개이므로, 2차원 공간에서 hyperplane이 직선으로 나타날 것이다.
특별히 kernel='linear'인 경우, coef_ 와 intercept_ 를 이용하여 hyperplane의 계수들을 구할 수 있다.
Decision Boundary
# set range of X and Y
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
# create meshgrid
h = 0.02 # step size in the mesh
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# predict by meshgrid
z = svm_clf.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
# plot the decision boundary
plt.gca().set_aspect('equal') # equal-ratio
plt.contourf(xx, yy, z, cmap=plt.cm.coolwarm, alpha=0.6)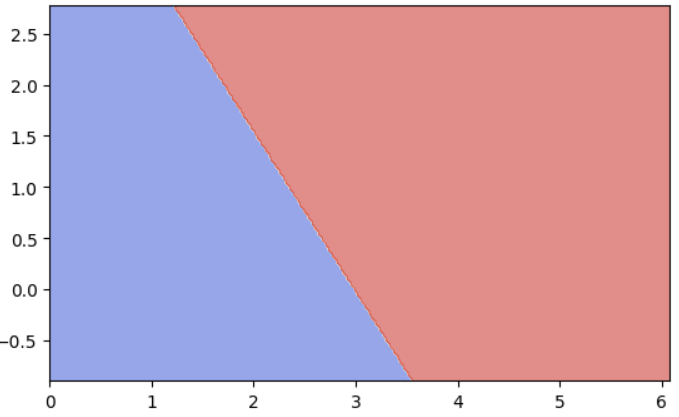
SVM 수식은 다음과 같다. (사이킷런에서는 $b$가 양수로 구현되어있다.)
\[ \mathbf{w}^\top \mathbf{x} + b = 0 \]
여기서 $\mathbf{w}$는 coefficient, $b$는 intercept이다.
사이킷런에서는 다음과 같이 멤버변수로 접근할 수 있다.
svm_clf.coef_
# array([[1.29411744, 0.82352928]])
svm_clf.intercept_
array([-3.78823471])2차원 벡터이므로 직선의 방정식을 이용하여 기울기를 구할 수 있다.
$\mathbf{w} = [w_0,. w_1]^\top$이고 $\mathbf{x} = [x_0, x_1]^\top$이므로
$w_0 x_0 + w_1 x_1 + b = 0 \Longleftrightarrow x_1 = -\cfrac{w_0}{w_1}x_0 -\cfrac{w_0}{w_1}b$ 를 이용하여 구할 수 있다.
해당 코드를 추가한 후 시각화하면 다음과 같다.
# set range of X and Y
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
# create meshgrid
h = 0.02 # step size in the mesh
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# predict by meshgrid
z = svm_clf.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
# plot the decision boundary
plt.gca().set_aspect('equal') # equal-ratio
plt.contourf(xx, yy, z, cmap=plt.cm.coolwarm, alpha=0.6)
# get hyperplane
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
# decision boundary
x0 = np.linspace(x_min, x_max, 200)
a = -w[0] / w[1]
y0 = a * x0 - (svm_clf.intercept_[0]) / w[1]
plt.plot(x0, y0, "k-", linewidth=2)
plt.axis([0, 5.5, 0, 2])
plt.show()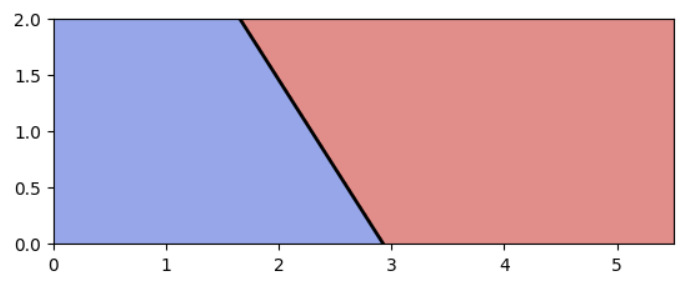
이제 support vector를 지나는 평행한 두 hyperplane(여기서는 직선)을 구해보자.
support vector는 다음과 같이 구할 수 있다.
svs = svm_clf.support_vectors_
'''
array([[1.9, 0.4],
[3. , 1.1]])
'''
plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
이제 margin을 구해보자.
margin = $\cfrac{1}{\Vert \mathbf{w} \Vert}$ 이고, $\mathbf{w}$는 정규화(normalized)되지 않았으므로, normal vector를 unit vector로 만들어 크기를 $1$로 만들고 margin만큼 곱하여 간격을 만든다.
# w = svm_clf.coef_[0]
margin = 1 / np.sqrt(np.sum(w **2))
unit_normal = w / np.sqrt(np.sum(w **2))
boundary_points = np.array(list(zip(x0, y0)))
lower_points = boundary_points - unit_normal * margin
upper_points = boundary_points + unit_normal * marginsupport vector를 지나는 직선은 이중선으로 하여 그리면 다음과 같다.
# set range of X and Y
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
# create meshgrid
h = 0.02 # step size in the mesh
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# predict by meshgrid
z = svm_clf.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
# plot the decision boundary
plt.gca().set_aspect('equal') # equal-ratio
plt.contourf(xx, yy, z, cmap=plt.cm.coolwarm, alpha=0.6)
# get hyperplane
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
# decision boundary
x0 = np.linspace(x_min, x_max, 200)
a = -w[0] / w[1]
y0 = a * x0 - (svm_clf.intercept_[0]) / w[1]
plt.plot(x0, y0, "k-", linewidth=2)
# calculate margin
# get paralles that pass through the support vectors
margin = 1 / np.sqrt(np.sum(w **2))
unit_normal = w / np.sqrt(np.sum(w **2))
boundary_points = np.array(list(zip(x0, y0)))
lower_points = boundary_points - unit_normal * margin
upper_points = boundary_points + unit_normal * margin
# plot the margin lines
plt.plot(x0, y0, "k-", linewidth=2)
plt.plot(lower_points[:, 0], lower_points[:, 1], "k--", linewidth=2)
plt.plot(upper_points[:, 0], upper_points[:, 1], "k--", linewidth=2)
# get support vectors and plot as pink (#FFAAAA)
svs = svm_clf.support_vectors_
plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
plt.axis([0, 5.5, 0, 2])
plt.show()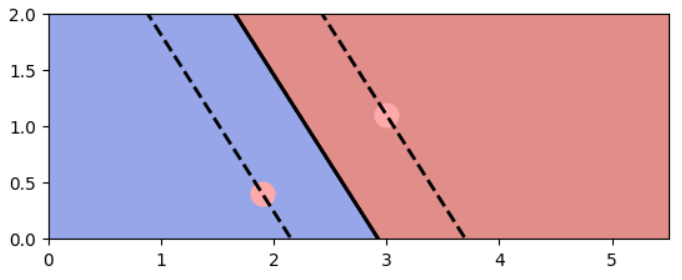
마지막으로 iris 데이터와 범례를 추가하면 다음과 같다.
# set range of X and Y
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
# create meshgrid
h = 0.02 # step size in the mesh
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# predict by meshgrid
z = svm_clf.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
# plot the decision boundary
plt.gca().set_aspect('equal') # equal-ratio
plt.contourf(xx, yy, z, cmap=plt.cm.coolwarm, alpha=0.6)
# get hyperplane
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
# decision boundary
x0 = np.linspace(x_min, x_max, 200)
a = -w[0] / w[1]
y0 = a * x0 - (svm_clf.intercept_[0]) / w[1]
plt.plot(x0, y0, "k-", linewidth=2)
# calculate margin
# get paralles that pass through the support vectors
margin = 1 / np.sqrt(np.sum(w **2))
unit_normal = w / np.sqrt(np.sum(w **2))
boundary_points = np.array(list(zip(x0, y0)))
lower_points = boundary_points - unit_normal * margin
upper_points = boundary_points + unit_normal * margin
# plot the margin lines
plt.plot(x0, y0, "k-", linewidth=2)
plt.plot(lower_points[:, 0], lower_points[:, 1], "k--", linewidth=2)
plt.plot(upper_points[:, 0], upper_points[:, 1], "k--", linewidth=2)
# get support vectors and plot as pink (#FFAAAA)
svs = svm_clf.support_vectors_
plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
# plot iris data
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 5.5, 0, 2])
plt.show()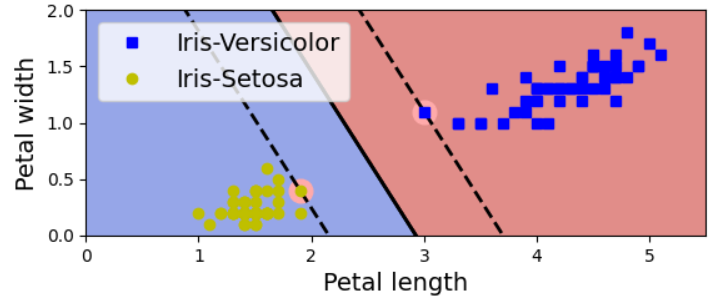
'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| [Ensemble] Basic Concept of Ensemble Methods, Bagging, Boosting (0) | 2023.05.12 |
|---|---|
| [Machine Learning] SVM in Python (2) - Margin, Regularization, Non-linear SVM, Kernel (0) | 2023.05.11 |
| [Machine Learning] SVM (Support Vector Machine) (0) | 2023.05.09 |
| [CS224w] Prediction with GNNs (0) | 2023.04.26 |
| [CS224w] Graph Augmentation (0) | 2023.04.24 |



