728x90
반응형


Linear Regression with Python
Setup
seaborn에 내장되어있는 차량 연비 데이터셋을 이용할 것이다.
import numpy as np
import scipy as sp
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df = sns.load_dataset('mpg')
df = df.dropna().reset_index(drop=True)
df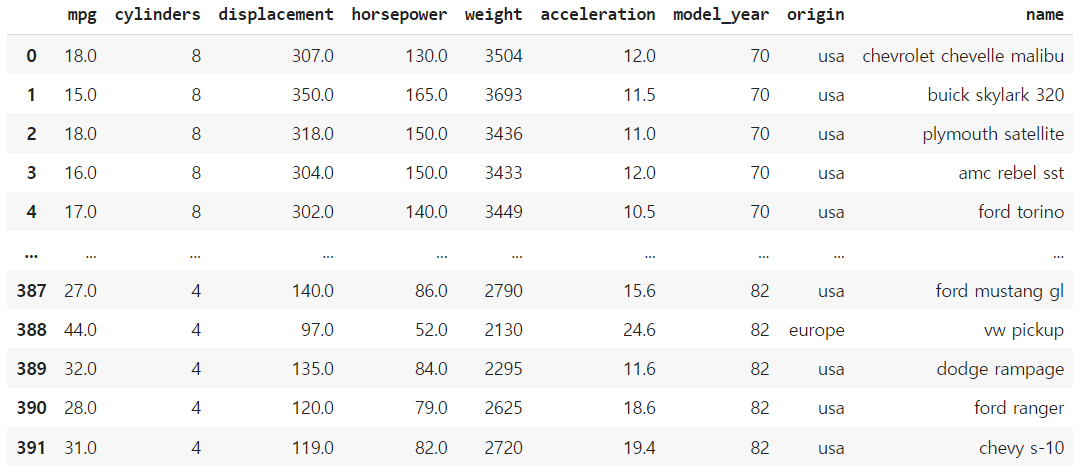
Select Features
sns.regplot(data=df, x='horsepower', y='mpg')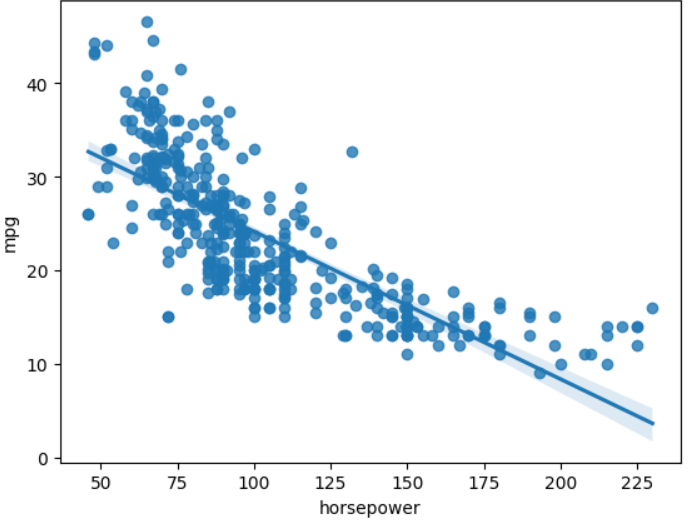
(1) statsmodels
R형식의 선형회귀 모델식을 작성한다.
형식은 "Y ~ x1 + x2 + x3" 와 같이 작성한다. 계수는 모델이 계산해줄 것이다.
우선 간단한 모델이므로 변수 하나인 선형회귀식을 모델링해보자.
import statsmodels.formula.api as smf
# create a fitted model
lm = smf.ols(formula='mpg ~ horsepower', data=data).fit()
#print model summary
print(lm.summary()) OLS Regression Results
==============================================================================
Dep. Variable: mpg R-squared: 0.606
Model: OLS Adj. R-squared: 0.605
Method: Least Squares F-statistic: 599.7
Date: Sat, 08 Apr 2023 Prob (F-statistic): 7.03e-81
Time: 20:50:38 Log-Likelihood: -1178.7
No. Observations: 392 AIC: 2361.
Df Residuals: 390 BIC: 2369.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 39.9359 0.717 55.660 0.000 38.525 41.347
horsepower -0.1578 0.006 -24.489 0.000 -0.171 -0.145
==============================================================================
Omnibus: 16.432 Durbin-Watson: 0.920
Prob(Omnibus): 0.000 Jarque-Bera (JB): 17.305
Skew: 0.492 Prob(JB): 0.000175
Kurtosis: 3.299 Cond. No. 322.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.선형모델 변수명 lm의 params를 통해 계수를 확인할 수 있다.
print(lm.params)
Intercept 39.935861
horsepower -0.157845
dtype: float64(2) scikit-learn linear_models
사이킷런 역시 많은 머신러닝 모델을 포함하고 있다.
from sklearn import linear_model
estimator = linear_model.LinearRegression(fit_intercept=True)
estimator.fit(data[['horsepower']], data[['mpg']])
print('Coef:', estimator.coef_) # Coef: [[-0.15784473]]
print('Intercept:', estimator.intercept_) # Intercept: [39.93586102]
두 라이브러리 모두 같은 계수임을 알 수 있다.
다만, sklearn은 모델의 학습만을 결과로 알 수 있다면, statsmodels는 근간이 R이기 때문에 보다 보고서에 필요한 결과들(R-square, p-value 등)까지 출력해준다.
Select Features - (2)
이제 연비와 상관있어보이는 변수 6개(실린더 수, 배기량, 마력, 중량, 가속력, 연차) 에 대해 선형관계를 갖는지 알아보자.
features = ['cylinders', 'displacement', 'horsepower', 'weight', 'acceleration', 'model_year']
fig, axes = plt.subplots(3, 2, figsize=(12, 10))
axes = axes.flatten()
for i, f in enumerate(features):
sns.regplot(data=df, x=f, y='mpg', ax=axes[i])
axes[i].set_xlabel(f)
plt.show()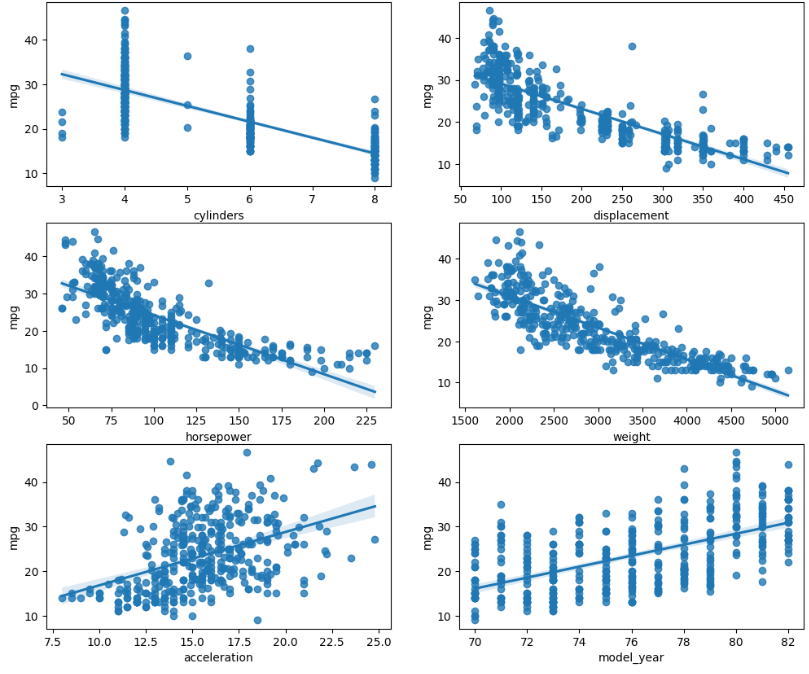
배기량, 마력, 중량에 대해서만 선형회귀 모델의 독립변수로 사용해보자.
(1) statsmodels
# create a fitted model
lm = smf.ols(formula='mpg ~ displacement + horsepower + weight', data=df).fit()
#print model summary
print(lm.summary())
print("\n", lm.params) OLS Regression Results
==============================================================================
Dep. Variable: mpg R-squared: 0.707
Model: OLS Adj. R-squared: 0.705
Method: Least Squares F-statistic: 312.0
Date: Sat, 08 Apr 2023 Prob (F-statistic): 5.10e-103
Time: 21:32:31 Log-Likelihood: -1120.6
No. Observations: 392 AIC: 2249.
Df Residuals: 388 BIC: 2265.
Df Model: 3
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------
Intercept 44.8559 1.196 37.507 0.000 42.505 47.207
displacement -0.0058 0.007 -0.876 0.381 -0.019 0.007
horsepower -0.0417 0.013 -3.252 0.001 -0.067 -0.016
weight -0.0054 0.001 -7.513 0.000 -0.007 -0.004
==============================================================================
Omnibus: 37.603 Durbin-Watson: 0.859
Prob(Omnibus): 0.000 Jarque-Bera (JB): 49.946
Skew: 0.707 Prob(JB): 1.43e-11
Kurtosis: 4.029 Cond. No. 1.73e+04
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.73e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
Intercept 44.855936
displacement -0.005769
horsepower -0.041674
weight -0.005352
dtype: float64(2) scikit-learn
estimator = linear_model.LinearRegression(fit_intercept=True)
estimator.fit(data[['displacement', 'horsepower', 'weight']], data[['mpg']])
print('Coef:', estimator.coef_)
print('Intercept:', estimator.intercept_)Coef: [[-0.00576882 -0.04167414 -0.00535159]]
Intercept: [44.8559357]
독립변수가 3개인 경우에도 statsmodels, sklearn 모두 계수가 동일한 결과를 얻었다.
728x90
반응형
'스터디 > 데이터사이언스' 카테고리의 다른 글
| Entropy의 의미 (정보이론) (0) | 2023.04.14 |
|---|---|
| [Pandas] iloc와 loc 차이점 (0) | 2023.04.12 |
| [Python] 데이터 시각화 (Basic) (0) | 2023.04.11 |
| [Pandas] Basic Statistics 살펴보기 (0) | 2023.04.10 |
| [Data Science] Grubb's test를 이용한 Outlier detection (0) | 2023.04.08 |


