
이번 글에서는 FP-Tree를 이용한 FP-Growth 알고리즘을 이용하여 frequent itemset mining을 해보자.
Motivation
Apriori principle의 마지막에서 서술했듯이, DB scan을 계속 반복해야하는 단점이 있다. 이는 여전히 비용이 큰 요소이다.
게다가 패턴이 긴 경우(long pattern) 은 DB scan을 반복하는것은 물론이고 candidate가 굉장히 많아진다는 문제가 있다.
결국 문제는 candidate generation이다!!
Heuristic
이때
이 방법을 이용하면, 재귀적으로 frequent itemset이 정의되므로 더이상 candidate generation은 필요하지 않다.
위 휴리스틱을 사용하기 위해 적합한 자료구조가 필요한데, 이를 FP-tree라고 한다.
FP는 Frequent-Pattern의 앞글자만 따온 것이다.
FP-Tree
(1) Construct FP-Tree
FP-Tree를 생성하는 순서는 크게 3가지이다.
- DB를 한번 스캔하여 frequent 1-itemset을 찾는다.
- frequent item을 (frequency 기준) 내림차순으로 정렬한다. 이를 f-list라 한다.
- DB를 다시 스캔하여, FP-Tree를 만든다.
Note: Apriori와 다르게, DB를 2번만 스캔한다는 장점이 있다.

DB를 한번 스캔하여 각 TID마다 f-list를 위와 같이 만들었다고 하자.
이제 3단계를 통해 FP-Tree를 만드는 과정을 살펴보자.
| TID | FP-Tree | Description |
| 100 |  |
f-list |
| 200 |  |
f-list 이때 접두사가 같은 경우는 그대로 빈도 카운트를 증가시킨다. 패턴이 일치하지 않는 경우에는, 트리를 분기하여 이어서 패턴을 작성한다. 이 경우, TID=200의 f-list에 |
| 500 |  |
5개의 transaction을 조회하여 최종적으로 생성된 FP-Tree이다. |
좋다! 이제 candidate itemset을 매번 생성하지 않고도 DB스캔 2번만으로도 모든 item의 패턴을 저장하는 FP-tree를 생성했다.
그런데 이제 FP-Tree를 이용해서 어떻게 Mining을 할 것인가?
(1) Conditional Pattern Base, pattern_base |
어떤 frequent itemset
Example
frequent itemset {m}에 대하여 {m}의 conditional pattern base는 다음과 같다.
- <f, c, a>: support=2
- <f, c, a, b>: support=1

(2) Conditional Pattern Tree, FP-tree |
pattern_base |
Example
frequent itemset {m}에 대하여 conditional pattern base는 위에서 보았듯이
- <f, c, a>: support=2
- <f, c, a, b>: support=1
이들을 접두사를 살리면서 더하면 <f:3, c:3, a:3, b:1>이다. 그러나 min_sup=3이므로 support가 작은 노드들은 탈락한다. 여기서는 {b}가 탈락한다. 따라서 conditional FP-Tree는 <f:3, c:3, a:3>이다.
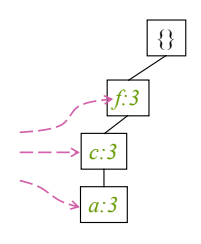
(3) Pattern Growth
이제 conditional FP-Tree를 통해 패턴을 찾을 것이다.
이 경우,
위에서 이어지는 예시에서, min_sup=3인 m의 conditional FP-Tree는 <f:3, c:3, a:3>이다.
재귀적으로 (am: 3), (cm: 3), (fm: 3)이 생성되고 또 재귀적으로 (cam: 3, fam: 3, fcm: 3) 그리고 마지막으로 (fcam: 3)을 얻는다.

FP-Growth vs Apriori
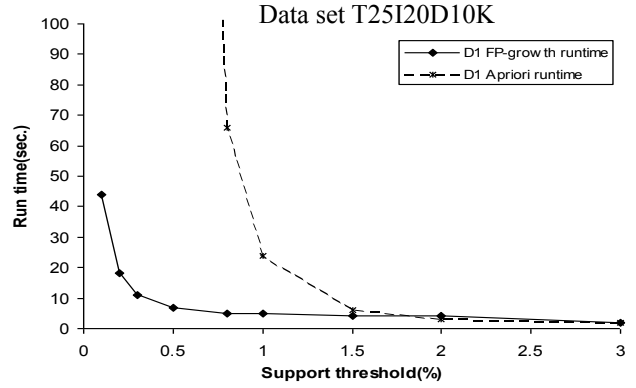
가장 큰 요인은 FP-Growth는 분할정복의 알고리즘으로 동작한다는 점이다. 따라서 작은 DB에서 작업을 한다고 볼 수 있다.
다른 요인들로는, candidate generation과 candidate test가 없다는 것, FP-Tree가 보다 더 압축된 자료구조인 점, DB scan이 단 2번만 이뤄진다는 것, 그리고 연산의 저비용(cheap operation)이다.
Example Answer
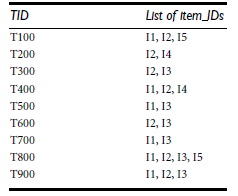
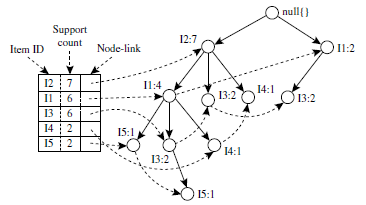
(1) FP-Tree
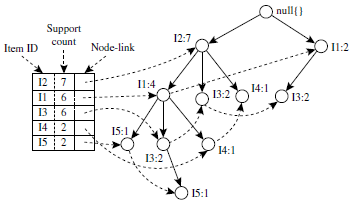
(2) Conditional Pattern Base, Conditional FP-Tree, Frequent Patterns
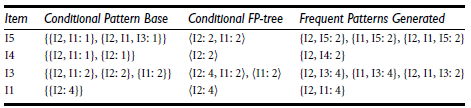
'스터디 > 데이터사이언스' 카테고리의 다른 글
| [Data Science] Association Rule Mining (6) Interesting Measures (0) | 2023.04.03 |
|---|---|
| [Data Science] Association Rule Mining (5) Rule Generation (0) | 2023.04.03 |
| [Data Science] Association Rule Mining (3) - Apriori + Hash Tree (0) | 2023.04.02 |
| [Data Science] Association Rule Mining (2) - Apriori principle (0) | 2023.04.01 |
| [Data Science] Association Rule Mining (1) - Introduction (0) | 2023.04.01 |



