[Data Science] Association Rule Mining (3) - Apriori + Hash Tree

 

 

이전 포스트(https://trivia-starage.tistory.com/88)에서 Brute-force의 성능을 높일 수 있는 방법 중 3번째에 대해서 설명해본다.

 

 

Support Conting

DB를 scan해서 각 candidate itemset이 support여부를 확인하는 방법이다.

그런데 각 transaction이 모든 candidate에 matching여부를 확인하기 위해 모든 candidate를 순회하는 문제가 발생한다.

이 때 비교횟수를 줄이기 위해 해시 기반 자료구조를 활용한다.

Figure 1. Support counting using hash structure

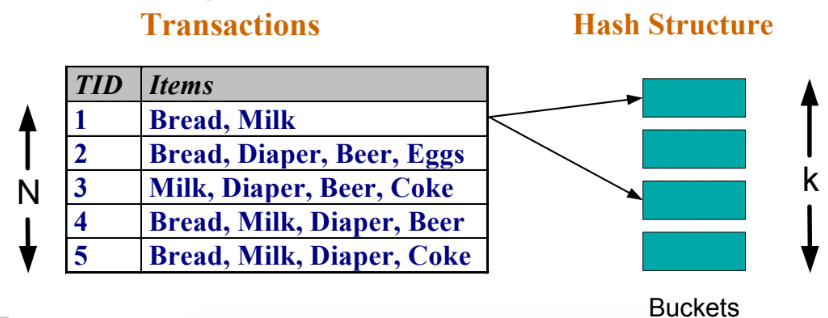
길이가 3인 15개의 candidate itemset이 있다고 하자.

{1 4 5}, {1 2 4}, {4 5 7}, {1 2 5}, {4 5 8}, {1 5 9}, {1 3 6}, {2 3 4}, {5 6 7}, {3 4 5}, {3 5 6}, {3 5 7}, {6 8 9}, {3 6 7}, {3 6 8}

이때 transaction (1, 2, 3, 4, 5, 6)에서 얼마나 많은 itemset이 만족할까?

 

 

우선 해시트리 자료구조를 이해하고, 다시 이 문제를 해결해보자.

Hash Tree

해시트리는 크게 2가지 특징을 갖는다.

1. Hash function($H$): item을 빠르게 찾을 수 있는 인덱스를 출력하는 해시함수.
2. Max leaf size: leaf node에 최대로 저장하는 itemset의 개수이다. 

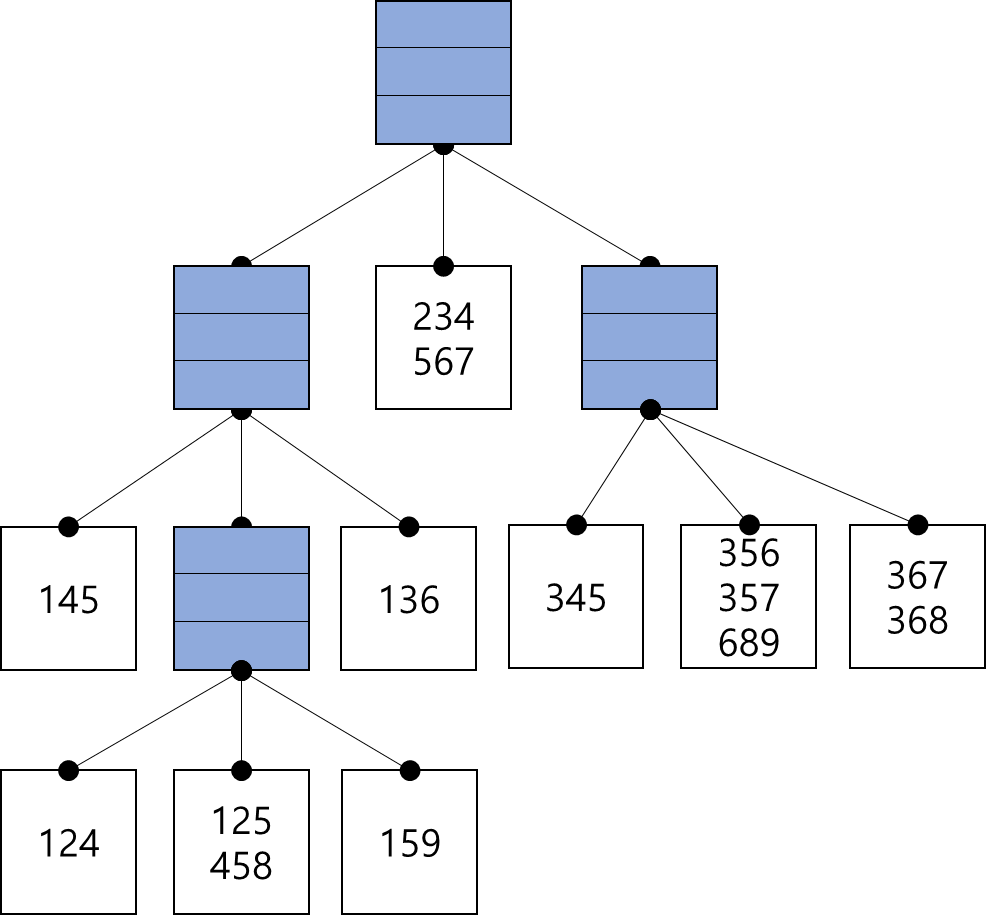
아래 그림은 해시함수가 $H(x) = x \mod 3$이고, max_leaf_size=3 인 해시트리에, 위 15개의 candidate itemsets이 저장된 모습이다.

Figure 2. Hash Tree

Hash Tree 만드는 과정

{1 4 5}, {1 2 4}, {4 5 7}, {1 2 5}까지 입력되면 이들 모두 해시함수의 출력이 같기 때문에 같은 버킷(bucket)에 담긴다. 그러나 max_leaf_size=3이므로 2번째 item으로 다시 해시값을 구한 후 leaf를 분할한다. (Figure 3 좌측)

{4 5 8}이 입력되면 또다시 [{1, 2, 4}, {4, 5, 7}, {1, 2, 5}, {4, 5, 8}]이 max_leaf_size를 벗어난다. 3번재 item으로 해시값을 구한 후 leaf를 분할한다. (Figure 3 중앙)

{1 5 9}, {1 3 6}, {2 3 4}, {5 6 7},은 입력되어도 max_leaf_size를 넘지 않으므로 leaf 분할 없이 해시트리에 그대로 저장된다. (Figure 3 중앙)

 

{3 4 5}, {3 5 6}, {3 5 7}, {6 8 9}, {3 6 7}, {3 6 8} 역시 위와 같은 과정을 통해 leaf를 split하여 확장한다.

Figure 3. Generating the Hash Tree

반응형

Subset Operation

이제 candidate itemset을 해시트리로 저장하여 탐색의 효율성을 높였다. 그렇다면 transaction이 입력되면 어떻게 candidate itemsets에서 찾을 수 있을까?

 

transaction 역시 hash함수에 따라 해시트리의 leaf node를 탐색한다. 

Figure 4. Subset Operation

Figure 5. Matching transasction

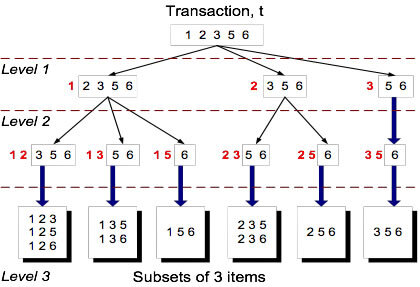
위 결과를 보면, 전체 candidate itemsets에서 6개의 leaf_node만 탐색하면 된다는 것을 알 수 있다.

 

알고리즘 성능에 영향을 주는 요소들

Choice of minimum support threshold

min_sup의 값이 작아질 수록 frequent itemsets은 더 많아진다. 이는 candidate의 개수도 같이 많아질 수 있다.

 

Dimensionality of dataset (the number of items)

고차원 데이터일 수록 각 item을 저장하기 위한 공간(memory, storage)가 더 필요하다.

frequent item의 수가 많아지면, 연산의 수는 물론이고 I/O 비용 역시 증가한다.

 

Size of Database

Apriori 알고리즘은 DB를 여러번 조회(scan, pass)하므로 알고리즘의 실행 시간은 (DB에 저장된) transaction의 수가 많을 수록 증가할 것이다.

 

Average transaction width ($w$)

밀도 높은 데이터셋일 수록 transaction width는 더 커질것이다. 이는 frequent itemsets의 최대 크기가 sparse한 경우보다 더 커질 수 있다. 즉, subset의 개수가 많아진다는 뜻이다. 이는 hash tree에서도 더 깊이 탐색할 것이다.