연속확률분포, Continuous Distribution

 

 

Keywords

연속확률변수, 확률밀도함수, 균등분포, 지수분포, 감마함수, 감마분포, 베타함수, 베타분포, 표준정규분포, 정규분포, 카이제곱분포

Continuous Random Variable, probability density function, density, density function, uniform distribution, exponential distribution, gamma function, gamma distribution, beta function, beta distribution, standard normal distribution, normal distribution, chi-squared distribution

 

 

Continuous Random Variable

확률변수 $X$가 모든 실수 $x \in \mathbb{R}$에 대하여 $P(X=x)=0$이면 연속확률변수하라고 한다.

Density function

$f: \mathbb{R} \to \mathbb{R}$이고 $f(x) \ge 0, \forall_x \in \mathbb{R}$이고 $\int_{-\infty}^{\infty}f(x)=1$이면 함수 $f(x)$는 밀도함수(density function)라고 한다.

Note. 책이나 강의마다 density function을 probability density function(확률밀도함수, pdf, PDF)라고도 한다.

Absolutely Continuous

확률변수 $X$가 density function $f$에 대하여 
\[ P(a \le X \le b) = \int_a^bf(x) dx \quad a \le b \]
이면 absolutely continuous라고 한다.

Note. density function $f$의 height(함숫값)은 확률과 전혀 상관이 없다. $f(x) > 1$이 가능하다.

매우 작은 양수 $\delta$에 대하여, $b=a+\delta$라 하자. 그러면

\[ P(a \le X \le a+\delta) = \int_a^{a+\delta} f(x) dx \approx \delta f(a) \]

따라서 다음이 성립한다.

확률변수 $X$가 absolutely continuous random variable일 때, $P(X=a)=0 \forall_a \in \mathbb{R}$이 성립한다.

PROOF) $P(X=a) = P(a \le X \le a) = \int_a^a f(x) dx = 0$

 

Uniform distribution, 균등분포, $X \sim U(\theta_1, \theta_2)$

\[ f(x) = \cfrac{1}{\theta_2 - \theta_1} I_{[\theta_1, \theta_2]} \]

 

Exponential distribution, 지수분포, $X \sim \text{Exp}(\lambda)$

\[ f(x) = \lambda e^{-\lambda x}, x \ge 0 \]

파라미터가 $\lambda$인 첫 번째 포아송 사건이 일어날 때까지 기다린 시간.

기계 등의 수명(life span)에 자주 사용되는 분포이다.

$\lambda = 2$인 지수분포

 

Memoryless Property, 무기억성(비기억성)

지수분포를 따르는 확률변수 $X$는 무기억성이다. 이미 $a$ 단위시간 지났을 경우는 무시할 수 있다.

\[ P(X \ge a + b | X \ge a) = P(X \ge b) \]

PROOF)

$P(X \ge x) = \int_{x}^{\infty} \lambda e^{-\lambda} dx = e^{-\lambda x} $ 이므로

$P(X \ge a + b | X \ge a) = \cfrac{P(X > a + b)}{P(X \ge a)} = \cfrac{e^{-\lambda (a + b)}}{e^{-\lambda a}} = e^{-\lambda b} = P(X \ge b)$

 

 

Gamma distribution, 감마분포, $X \sim \Gamma(\alpha, \lambda)$

\[ f(x) = \cfrac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha - 1} e^{-\lambda x} \]

Gamma function, 감마함수
\[ \Gamma(\alpha) = \int_0^{\infty}t^{\alpha - 1}e^{-t} dt, \quad \alpha > 0 \]

감마함수의 몇가지 성질
(1) $\Gamma(\alpha + 1) = \alpha \Gamma(\alpha)$
    (1.1) 특히 자연수 $n$에 대하여 $\Gamma(n) = (n-1)!$ 이다.
    (1.2) $\Gamma(1) = 1 (\because 0! = 1)$
(2) $\Gamma(0.5) = \sqrt{\pi}$

Note 1: 책에 따라 감마함수의 두 번째 파라미터를 $\beta = \cfrac{1}{\lambda}$로 표기할 수 있다.
Note 2: 감마함수는 density function이 아니다. 

 

Gamma function example

위의 (2.2)에 따라 감마함수의 $0.5$ 단위는 손으로 계산이 가능하다.

$\Gamma(2.5) = \frac{3}{2}\Gamma(\frac{1}{2}) = \frac{3}{2} \frac{1}{2} \Gamma(\frac{1}{2}) = \frac{3}{4} \sqrt{\pi}$

 

Gamma density는 아래와 같이 정의된다. (이것이 감마분포의 pdf이다)

\[ f(x) = \cfrac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha - 1} e^{-\lambda x} \]

 

지수분포는 감마분포의 $\alpha=1$인 경우로 해석할 수 있다. ($\text{Exp}(\lambda) = \Gamma(1, \lambda)$)

 

 

kernel of density

감마분포에 사용되는 PDF는 감마함수의 내부의 피적분함수의 적분 결과가 $1$이 되도록 정규화한다고 생각하면 된다.

$\cfrac{\lambda^{\alpha}}{\Gamma(\alpha)}$를 Normalizing constant, $x^{\alpha-1}e^{-\lambda x}$를 kernel of density라고도 부른다.

 

kernel of density로 이루어진 적분은 부분적분을 이용하지 않고도 간단하게(?) 계산할 수 있다.

$x^{2}e^{-3x}$은 $2 = \alpha - 1, 3=\lambda$로 해석하면 $\Gamma(3, 3)$의 kernel이므 $\displaystyle\int_{0}^{\infty}x^2 e^{-3x} dx = \cfrac{\Gamma(3)}{3^3} = \cfrac{2}{27}$ 이다.

 

 

감마분포의 확률밀도함수

$\alpha > 0$에 따라 모양이 바뀌므로 shape parameter라고도 부른다.

(1) $\alpha < 1$ $x \to 0$일 때 $\infty$로 발산, 아래로 감소하는 그래프

(2) $\alpha = 1$ 지수분포와 같은 그래프

(3) $\alpha > 1$ 왼쪽으로 치우친 그래프

 

여러가지 감마분포의 확률밀도함수

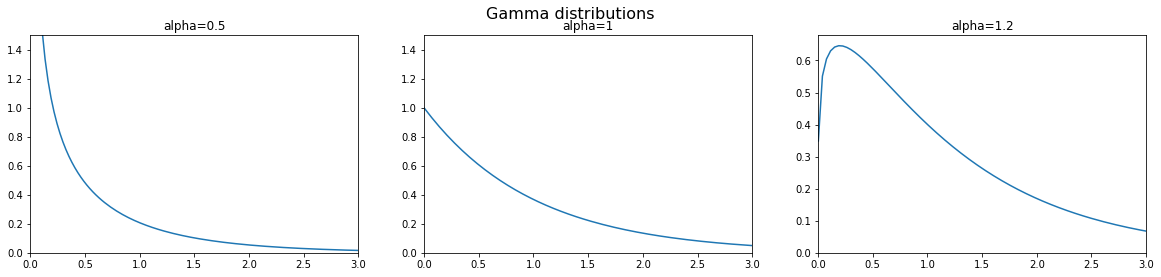
import numpy as np
from scipy.stats import beta
from scipy.stats import gamma

import matplotlib.pyplot as plt

params = [0.5, 1, 1.2]
x = [np.linspace(gamma.ppf(0.001, alpha), gamma.ppf(0.999, alpha), 200) for alpha in params]

fig, axes = plt.subplots(1, len(params), figsize=(20 ,4))
fig.suptitle('Gamma distributions', fontsize=16)

for i in range(len(params)):
  axes[i].plot(x[i], gamma.pdf(x[i], params[i]))
  axes[i].set_ylim(0, 1.5)
  axes[i].set_xlim(0, 3)
  if params[i] > 1:
    axes[i].set_ylim(0, max(gamma.pdf(x[i], params[i]) * 1.05))
  axes[i].set_title(f'alpha={params[i]}')

 

Beta distributin, 베타분포, $X \sim Beta(\alpha, \beta)$

베타함수($B$)는 아래와 같이 정의된다.

\[ B(\alpha, \beta) = \cfrac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)} = \int_0^1 t^{\alpha - 1}(1-t)^{\beta - 1} dt \]

 

Bayesian statistics에서 자주 사용된다.

 

베타분포는 베타함수의 피적분함수의 적분결과가 $1$이 되도록 정규화한다고 생각하면 된다.

\[ f(x) = \cfrac{x^{\alpha - 1} (1-x)^{\beta - 1}}{B(\alpha, \beta)} = \cfrac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta)}x^{\alpha - 1} (1-x)^{\beta - 1} , \ 0 \ge x \le 1 \]

 

kernel of density

베타분포에서도 베타함수 자체가 density하지 않기 때문에 적분의 결과가 $1$이 되도록 정규화해준다고 생각하면된다. 감마분포에서와 마찬가지고, $x^{\alpha - 1}(1-x)^{\beta - 1}$은 kernel이고, 분모의 $Beta(\alpha, \beta)$는 normalizing constant라고도 한다.

 

(1) $\displaystyle\int_0^1 x^7 (1-x)^8 dx$를 구해보자. kernel은$x^7(1-x)^8$, normalizing constant는 $Beta(8, 9)$이므로

\[ \displaystyle\int_0^1 x^7(1-x)^8 dx = Beta(8, 9) = \cfrac{7! \ 8!}{16!} \]

 

베타분포의 확률밀도함수

(1) $\alpha < 1, \beta < 1$이면 아래로 볼록한 그래프.

(2) $\alpha, \beta$ 중 하나는 $1$보다 크고, 하나는 $1$보다 작은 양수일 때, 한 쪽으로 증가/감소하는 그래프

    (2.1) $0 < \beta < 1 < \alpha$ 이면 $x \to 1$일 때 $\infty$로 발산하는 증가하는 그래프

    (2.2) $0 < \alpha < 1 < \beta$ 이면 $x \to 0$일 때 $\infty$로 발산하는 감소하는 그래프 

(3) $\alpha > 1, \beta > 1$이면 위로 볼록한 그래프

여러가지 베타분포의 확률밀도함수

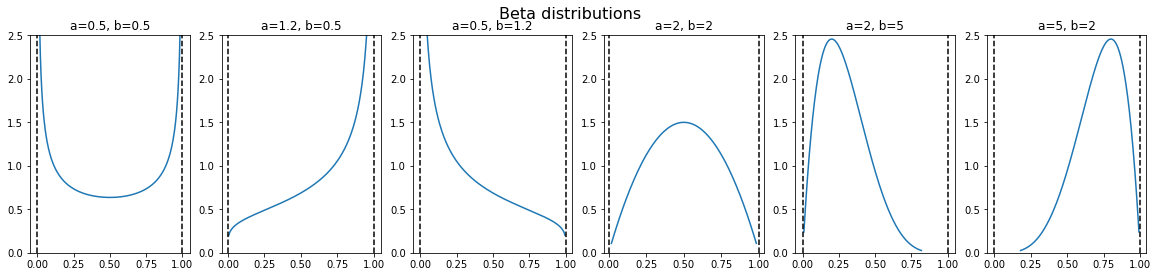
import numpy as np
from scipy.stats import beta
from scipy.stats import gamma

import matplotlib.pyplot as plt

params = [(0.5, 0.5), (1.2, 0.5), (0.5, 1.2), (2, 2), (2, 5), (5, 2)]

fig, axes = plt.subplots(1, len(params), figsize=(20 ,4))
fig.suptitle('Beta distributions', fontsize=16)

for ax, (a, b) in zip(axes, params):
  x = np.linspace(beta.ppf(0.001, a, b), beta.ppf(0.999, a, b), 200)
  ax.plot(x, beta.pdf(x, a, b))
  ax.set_ylim(0, 2.5)
  ax.axvline(x=0, linestyle='--', color='black')
  ax.axvline(x=1.0, linestyle='--', color='black')
  ax.set_title(f'a={a}, b={b}')

 

참고로 $B(1, 1) = U(0, 1)$과 같다.

 

Normal distribution, 정규분포, $X \sim N(\mu, \sigma^2)$

표준정규확률밀도함수(standard normal density)는 $\phi$로 표기하고 아래와 같다.

\[ \phi(x) = \cfrac{1}{\sqrt{2 \pi}}e^{-x^2/2} \]

 

정규분포함수는 아래와 같다.

\[ f(x) = \cfrac{1}{\sigma}\phi(\cfrac{x-\mu}{\sigma}) \cfrac{1}{\sigma \sqrt{2 \pi}}e^{-\cfrac{(x-\mu)^2}{2\sigma^2}} \]

 

※ $\phi(x)$가 density function임을 보이는 방법은 크게 2가지 있다.

(1) $I = \displaystyle\int_{-\infty}^{\infty}e^{-x^2} dx$라하면

\[ I^2 = \left( \int_{-\infty}^{\infty}e^{-x^2/2}dx \right)^2 = \left( \int_{-\infty}^{\infty}e^{-x^2/2}dx \right) \left( \int_{-\infty}^{\infty}e^{-y^2/2}dy \right) = \iint_{-\infty}^{\infty}e^{-(x^2+y^2)} dxdy \] 

$x = r \cos \theta, \ y = r \sin \theta$로 극좌표로 변환하면 적분구간도 바뀌어서

\[ I^2 = \int_{0}^{2\pi}\int_{0}^{\infty}e^{-r^2/2}r \ dr d\theta \]

$u = \cfrac{r^2}{2}$로 치환하면 $du = rdr$이므로 치환적분과 이상적분을 하면

\[ I^2 = \int_{0}^{2\pi}\int_{0}^{\infty}d^{-u}du d\theta = \int_{0}^{2\pi} \left( -\lim_{t \to \infty}[e^{-u}]_{u=0}^{u=t} \right) d\theta = \int_{0}^{2\pi}1 d\theta = 2\pi \]

$e^{-x^2/2} > 0$이므로 $I = \sqrt{2\pi}$이다.

 

(2) 대칭성을 이용하여 $\displaystyle\int_{-\infty}^{\infty} \phi(x)dx = 2 \displaystyle\int_{0}^{\infty} \phi(x)dx$

$u = \cfrac{1}{2}x^2$로 치환하면 $du = xdx$이므로 $dx = \cfrac{1}{x}du = \cfrac{1}{\sqrt{2u}}du$

\[ 2\int_{0}^{\infty}\phi(x) dx = 2\int_{0}^{\infty}\cfrac{1}{\sqrt{2\pi}}\cfrac{1}{\sqrt{2u}}e^{-u}du  = \cfrac{1}{\sqrt{\pi}}\int_{0}^{\infty}u^{-\frac{1}{2}}e^{-u} \]

$u^{-\frac{1}{2}}e^{-u}$는 $\alpha=\frac{1}{2}, \lambda=1$인 감마함수의 kernel이고 $\Gamma(\frac{1}{2})=\sqrt{\pi}$이므로

\[ \cfrac{1}{\sqrt{\pi}}\int_{0}^{\infty}u^{-\frac{1}{2}}e^{-u} = \cfrac{1}{\sqrt{\pi}} \sqrt{\pi} = 1 \]

 

kernel of density

앞의 density function들과 마찬가지로 $\cfrac{1}{\sigma \sqrt{2 \pi}}$를 normalizing constant, $e^{-(x - \mu) / 2\sigma^2}$를 kernel이라 부른다.

 

앞의 density function의 예시와 마찬가지로, kernel을 이용하여 몇가지 함수의 적분을 쉽게(?) 구할 수 있다.

(1) $\displaystyle\int_{-\infty}^{\infty}e^{-3x^2} dx$를 구해보자. $e^{-3x^2}$은 $N(0, 1/6)$의 kernel이므로 normalizing constant를 곱하면 

\[ \displaystyle\int_{-\infty}^{\infty}e^{-3x^2} dx = \sqrt{2\pi} \sqrt{\cfrac{1}{6}} \]

(2) $\displaystyle\int_{-\infty}^{\infty}e^{-x^2+2x} dx$를 구해보자. 피적분함수는 $N(1, (\cfrac{1}{\sqrt{2}})^2)$의 kernel이고 평행이동을 고려하면

\[ \displaystyle\int_{-\infty}^{\infty}e^{-x^2+2x} dx = \displaystyle\int_{-\infty}^{\infty}e^{-(x-1)^2} \cdot e \ dx = \sqrt{\pi} \cdot e \]

 

Empirical Rule

68-95-99.7 규칙이라고도 한다. (그 쉽다는 GRE quantitative에서도 이 세 숫자는 외워야 풀 수 있다.)

• $P(\mu - \sigma < X < \mu + \sigma) = 0.68$
• $P(\mu - 2\sigma < X < \mu + 2\sigma) = 0.95$
• $P(\mu - 3\sigma < X < \mu + 3\sigma) = 0.997$

 

Chi-squared distribution, $\chi^2(k)$

Recall that

\[ Gamma(\alpha, \lambda) = \cfrac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha - 1}e^{-\lambda x}, \ x>0, \alpha > 0, \lambda > 0 \]

 

카이제곱 분포는 자유도(degrees of freedom)이라는 파리미터만 있고, 감마함수의 특별한 형태로 정의한다.

\[ \chi^2(k) = Gamma \left( \frac{k}{2}, \frac{1}{2} \right) \]

따라서 density function은

\[ f(x) = \cfrac{\left(\cfrac{1}{2}\right)^{(\cfrac{k}{2})} }{\Gamma \left(\cfrac{k}{2}\right)} x^{\left( \cfrac{k}{2} \right) - 1}e^{-\cfrac{1}{2}x} \]