728x90
반응형
파이썬 코드로 이산확률분포가 파라미터에 따라 어떻게 그려지는지 알아보자.
import numpy as np
from scipy.special import binom, comb
import matplotlib.pyplot as pltBinomial Distribution, 이항분포
def binomial(x, n, theta):
return comb(n, x) * (theta ** x) * ((1 - theta) ** (n - x))
params = [(20, 0.3), (20, 0.5), (20, 0.7), (26, 0.9)]
fig, axes = plt.subplots(1, 4, figsize=(24, 4))
for ax, (n, theta) in zip(axes, params):
print(n, theta)
probs = []
for x in range(n + 1):
probs.append(binomial(x, n, theta))
ax.bar(range(n + 1), probs)
ax.set_title(f'n={n}, theta={theta}')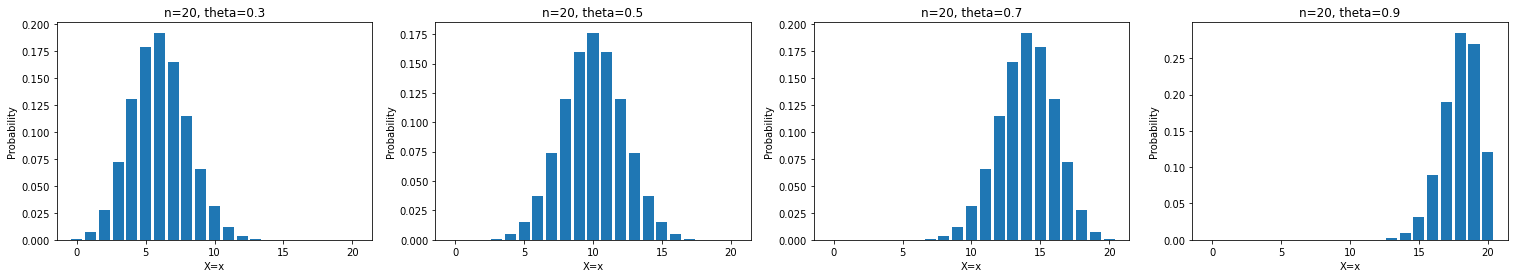
Geometric distribution, 기하분포
기하분포는 단조감소하는 형태이다.
def geometric(x, theta):
return ((1 - theta) ** x) * theta
params = [(10, 0.3), (10, 0.5), (10, 0.7), (10, 0.9)]
fig, axes = plt.subplots(1, 4, figsize=(26, 4))
for ax, (n, theta) in zip(axes, params):
probs = []
for x in range(n + 1):
probs.append(geometric(x, theta))
ax.bar(range(n + 1), probs)
ax.set_title(f'theta={theta}')
ax.set_xlabel('X=x')
ax.set_ylabel('Probability')
Negative-Binomial distribution, 음이항분포
def neg_bin(x, r, theta):
return comb(r - 1 + x, x) * (theta ** r) * ((1 - theta) ** x)
params = [(10, 2, 0.6), (12, 4, 0.6), (20, 6, 0.6), (20, 8, 0.6)]
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
for ax, (n, r, theta) in zip(axes, params):
probs = []
for x in range(n + 1):
probs.append(neg_bin(x, r, theta))
ax.bar(range(n + 1), probs)
ax.set_title(f'r={r}, theta={theta}')
ax.set_xlabel('X=x')
ax.set_ylabel('Probability')
Poisson distribution, 포아송분포
포아송분포는 단 하나의 peak가 존재한다.
포아송은 수식의 시작이 이항분포이므로 역시 이항분포와 비슷한 분포를 갖는다.
def poisson(x, lambda_):
return ((lambda_ ** x) * np.math.exp(-lambda_)) / np.math.factorial(x)
lambdas = [1, 3, 5, 7]
fig, axes = plt.subplots(1, 4, figsize=(26, 4))
for ax, (lambda_) in zip(axes, lambdas):
probs, n = [], lambda_ * 3
for x in range(n + 1):
probs.append(poisson(x, lambda_))
ax.bar(range(n + 1), probs)
ax.set_title(f'lambda={lambda_}')
ax.set_xlabel('X=x')
ax.set_ylabel('Probability')
Hypergeometric distribution, 초기하분포
초기하분포는 하나의 peak가 존재한다
그리고 $N$과 $M$이 충분히 크면 이항분포에 근사하는 것도 확인할 수 있다.
def hyper_geo(x, n, N, M):
return (comb(M, x) * comb(N - M, n - x)) / comb(N, n)
params = [(5, 15, 5), (5, 15, 7), (50, 100, 80), (300, 500, 70)] # (n, N, M)
fig, axes = plt.subplots(1, 4, figsize=(26, 4))
for ax, (n, N, M) in zip(axes, params):
probs = []
x_min = max(0, n + M - N)
x_max = min(n, M)
for x in range(x_min, x_max + 1):
probs.append(hyper_geo(x, n, N, M))
ax.bar(range(x_min, x_max + 1), probs)
ax.set_title(f'n={n}, N={N}, M={M}')
ax.set_xlabel('X=x')
ax.set_ylabel('Probability')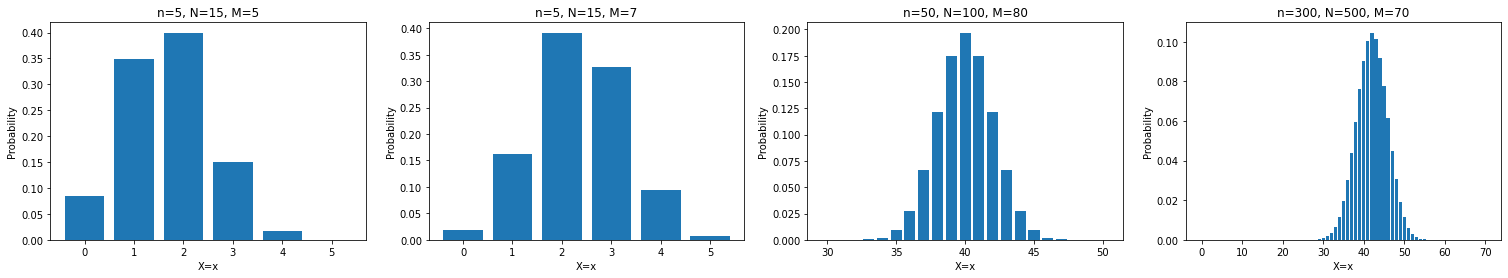
728x90
반응형
'스터디 > 확률과 통계' 카테고리의 다른 글
| 누적분포함수, Cumulative Distribution Function (CDF) (0) | 2023.03.21 |
|---|---|
| 연속확률분포, Continuous Distribution (0) | 2023.03.16 |
| Discrete Random Variables and Distributions (확률변수, 이산확률분포) (0) | 2023.03.09 |
| 중앙값 추정하기. Median of Grouped Data using Median Class (0) | 2023.03.07 |
| Ch1. Probability Models (0) | 2023.03.04 |


