Comparing Two Population Means
Two Sample Problems
이번 포스트에서는 두 모집단의 차이를 살펴볼 것이다.
영어로는 two-sample problem이라 한다.
두 모집단 A, B가 있다고 하자.
$x_1, \dots, x_n$은 A에서 얻은 데이터(observed data)이고, $y_1, \dots, y_m$은 B에서 얻은 데이터라 하자.
수학적으로 $x_i$는 $F_A(x)$에서, $y_i$는 $F_B(x)$에서 추출된 샘플이라 할 수 있다.
두 모집단의 차이를 말할 때, $F_A(x), F_B(x)$의 차이를 구하면 되지 않느냐고 할 수 있다.
그러나 $H_0: F_A=F_B \text{ vs. } H_A: F_A \neq F_B$ 이렇게는 하면 답이 없다.
두 분포가 동일(identical)하다면, 두 모집단의 모평균이 같다고 할 수 있을 것이다.
(물론 두 모집단의 모분산을 비교할 수도 있다)
만약 데이터분석으로 $\mu_A \neq \mu_B$임을 알 수 있다면, 우리는 A, B 분포가 다르다고 할 것이다.
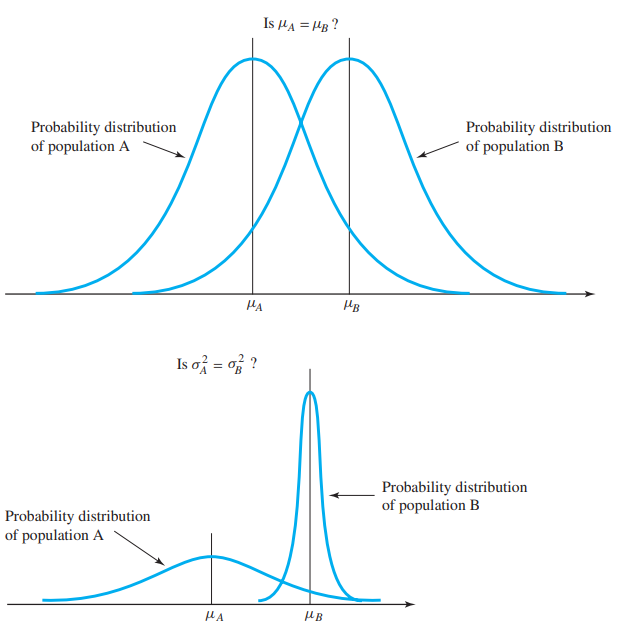
이제 우리는 $H_0: \mu_A = \mu_B$를 testing하면 된다.
p-value가 작다면, $H_0$가 not plausible하므로 두 모집단이 다르다는 충분한 증거(sufficient evidence)가 있다고 할 수 있다.
p-value가 크다면, 두 모집단이 다르다는 증거가 충분하지 않다고 할 수 있다.
그렇다면 어떻게 p-value를 계산할 것인가?
(one-sample의 과정처럼, test statistics를 구하고, 이 statistic이 어떤 분포를 따르는지 알면 된다)
Paired Samples vs. Independent Samples
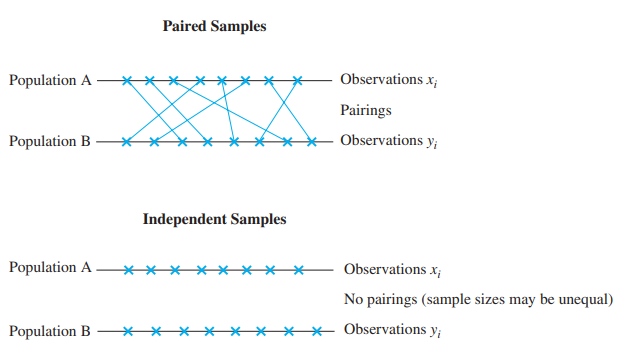
two-sample의 경우, 두개의 샘플 방법이 있다: paried와 independent samples
paired sample의 예시로, 치료법(약 처방, 치료 등)의 효과가 있다.
동일한 환자(피험체)에게 치료법을 적용하여, 효과가 있는지(두 분포가 다른지) 없는지( 두 분포가 같은지) 살펴본다.
이 경우 데이터는 $(x_1, y_1), \dots, (x_n, y_n)$이 되고 당연히 두 모집단에서 추출한 샘플의 크기는 같다.
independent sample의 경우, 각 모집단에서 샘플링을 독립적으로 한 것이다.
그러므로 두 모집단에서 추출한 샘플의 크기는 다를수 있다.
Analysis of Paired Samples
$(x_1, y_1), \dots, (x_n, y_n)$의 데이터를 얻었다고 하자.
두 모집단의 차이를 구하기 위해 $z_i = x_i - y_i$를 이용할 것이다.
이 경우, one-sample에서 공부한 가설 검정방법과 동일하다.
수학적 배경
$\mu_A, \mu_B$를 treatment A/B effect라하고, $\gamma_i$를 $i$번째 환자의 고유 효과(subject effect), 그리고 $\epsilon^A, \epsilon^B$를 A/B의 random error라 하자. 그러면
\[ x_i = \mu_A + \gamma_i + \epsilon^A \quad y_i = \mu_B + \gamma_i + \epsilon^B \]
그려면 $z_i = \mu_A - \mu_B + \epsilon^{A} - \epsilon^B$이고, error의 기댓값은 $0$이므로 사라진다.
subject effect $\gamma$가 없으므로 $\mu = \mu_A - \mu_B$는 $\gamma$에 의존하지 않는다.
setting
- $z_1, \dots, z_n \text{ where } z_i = x_i - y_i$
- $H_0: \mu = 0 \text{ vs. } H_A: \mu \neq 0$
- t-statistics = $\cfrac{\bar{z} - \mu}{s / \sqrt{n}}$
- p-value = $2 \times P(T > t)$ where $T \sim t_{n-1}$
- 신뢰구간: $\mu = \mu_A - \mu_B \in \left( \bar{z} \pm t_{\alpha/2, n-1} \cfrac{s}{\sqrt{n}} \right)$
- 무엇이 $H_0$의 $\mu$인지 명시해야한다. 여기서는 $\mu = \mu_A - \mu_B$로 difference를 명시.
Analysis of Independent Samples
$n$과 $m$을 각각 모집단 A, B에서 얻은 데이터의 크기(표본크기, sample size)라 하자.
$x_1, \dots, x_n$: A에서 얻은$n$개의 데이터
$y_1, \dots, y_m$: B에서 얻은 $m$개의 데이터
$\bar{x},\ \bar{y}$: A, B에서 얻은 데이터의 표본평균(sample mean)
$s_x,\ s_y$: A, B에서 얻은 데이터의 표본표준편차(sample deviation)
$\mu_A - \mu_B$의 point estimator는 $\bar{x} - \bar{y}$임을 이용하자.
그러면 $Var(\bar{X}) = \cfrac{\sigma_A^2}{n}$, $Var(\bar{Y}) = \cfrac{\sigma_B^2}{m}$
그러므로 $\overline{X} - \overline{Y} \approx N \left( \mu_A - \mu_B, \frac{\sigma_A^2}{n} + \frac{\sigma_B^2}{m} \right)$
Standard Error는 $\text{S.E.}(\overline{X} - \overline{Y}) = \sqrt{ \frac{\sigma_A^2}{n} + \frac{\sigma_B^2}{m} }$
그러나 우리는 모분산 $\sigma_A^2, \sigma_B^2$를 모르기 때문에
\[ \text{S.E.}(\overline{X} - \overline{Y}) = \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m} } \]
모분산 $\sigma_A^2, \sigma_B^2$에 대한 정보에 따라 검정 방법이 달라진다.
간단히 정리하면 다음과 같다.
(1) General Procedure (two-sample t-procedure, unequal variances)
$\sigma_A^2 \neq \sigma_B^2$ 일 때 사용한다. 이때 standard error는
\[ \text{s.e.}(\overline{x} - \overline{y}) = \sqrt{ \frac{s_x^2}{n} + \frac{s_y^2}{m} } \]
(2) Pooled Variance Procedure (two-sample t-procedure, equal variances)
pooled variance의 estimator를 $s_p^2$라 하고,
\[ \text{s.e.}(\overline{x} - \overline{y}) = s_p \sqrt{ \frac{1}{n} + \frac{1}{m} } \]
이때 $s_p^2$는 pooled variance로
\[ \hat{\sigma}^2 = s_p^2 = \frac{(n-1)s_x^2 + (m-1)s_y^2}{n+m-2} \]
(3) Two-sample z-procedure
$\sigma_A^2$와 $\sigma_B^2$가 알려져(known)있다면, two-sample z-test를 한다.
General Procedure (Smith-Satterthwaite test)
$\mu_A - \mu_B$의 point estimator는 $\bar{x} - \bar{y}$이므로 standard error는
\[ \text{s.e.}(\bar{x} - \bar{y}) = \sqrt{ \frac{s_x^2}{n} + \frac{s_y^2}{m} } \]
p-value는 t-분포를 이용하여 계산한다. t-분포의 자유도는 다음과 같다.
\[ \nu = \cfrac{\left( \cfrac{s_x^2}{n} + \cfrac{s_y^2}{m} \right)^2}{ \frac{s_x^4}{n^2(n-1)} + \frac{s_y^2}{m^2(m-1)} } \]
대부분의 경우 $\mu$는 실수값이 나오는데, 자유도는 정수이므로 floor로 버림한다. ($\nu := \lfloor \nu \rfloor$)
또다른 방법으로 $v = \min\{n,m\}-1$이 있지만, 정확도가 떨어진다고 한다.
two-sided $1-\alpha$ level confidence interval은 다음과 같다.
\[ \mu_A - \mu_B \in \left( \bar{x}-\bar{y} \pm t_{\alpha/2, \nu} \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m}} \right) \]
one-sided confidence interval은
\[ \mu_A - \mu_B \in \left( -\infty, \ \bar{x}-\bar{y} + t_{\alpha, \nu} \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m}} \right) \]
또는
\[ \mu_A - \mu_B \in \left( \bar{x}-\bar{y} - t_{\alpha, \nu} \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m}},\ \infty \right) \]
이다.
일반화
임의의 상수 $\delta$에 대하여 (대부분 $\delta = 0$이다)
\[ H_0: \mu_A - \mu_B = \delta \text{ vs. } H_A: \mu_A - \mu_B \neq \delta \]
라 하자. 이때 t-statistics는
\[ t = \cfrac{\bar{x} - \bar{y} - \delta}{\sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m} }} \]
(자유도 $\nu$ 계산은 동일)
two-sided testing이라면
- p-value = $2 \times P(T > |t|)$ where $T \sim t_v$
- rejection region: $|t| > t_{\alpha/2, \nu}$
- confidence interval: $\mu_A - \mu_B \in \left( \bar{x}-\bar{y} \pm t_{\alpha/2, \nu} \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m} } \right)$
one-sided testing이면($H_0: \mu_A - \mu_B \le \delta \text{ vs. } H_A: \mu_A - \mu_B > \delta$)
- p-value = $P(T > t)$ where $T \sim t_v$
- rejection region: $T > t_{\alpha, \nu}$
one-sided testing이면($H_0: \mu_A - \mu_B \ge \delta \text{ vs. } H_A: \mu_A - \mu_B < \delta$)
- p-value = $P(T < t)$ where $T \sim t_v$
- rejection region: $T < -t_{\alpha, \nu}$
Pooled Variance Procedure
두 모집단 A, B의 모분산이 동일할 때(혹은 거의 비슷할 때, euqual or quite similar) pooled variance를 이용한 검정 방법이다.
두 모분산이 $\sigma^2$로 동일하다고 하자. ($\sigma_A^2 = \sigma_B^2 = \sigma^2$)
$\cfrac{(n-1)s_x^2}{\sigma^2} \sim \chi^2_{n-1}$이고 $ \cfrac{(m-1)s_y^2}{\sigma^2} \sim \chi^2_{m-1} $이고 이 둘은 독립이므로 이들의 합 $ \cfrac{(n-1)s_x^2}{\sigma^2} + \cfrac{(m-1)s_y^2}{\sigma^2} \sim \chi^2_{n+m-2}$ 이다.
모분산의 point estimator는
\[ \hat{\sigma}^2 = s_p^2 = \cfrac{(n-1)s_x^2 + (m-1)s_y^2}{n+m-2} \]
standard error는
\[ \text{s.e.}(\bar{x}-\bar{y}) = \sqrt{\frac{\sigma_A^2}{n} + \frac{\sigma_B^2}{m} } = \sigma \sqrt{\frac{1}{n} + \frac{1}{m}} \]
estimated standard error는 위 식에 $s_p$를 대입한다.
\[ \text{s.e.}(\bar{x}-\bar{y}) = s_p \sqrt{\frac{1}{n} + \frac{1}{m}} \]
$\bar{X}-\bar{Y} \approx N \left(\mu_A - \mu_B, \frac{\sigma_A^2}{n} + \frac{\sigma_B^2}{m} \right)$이므로
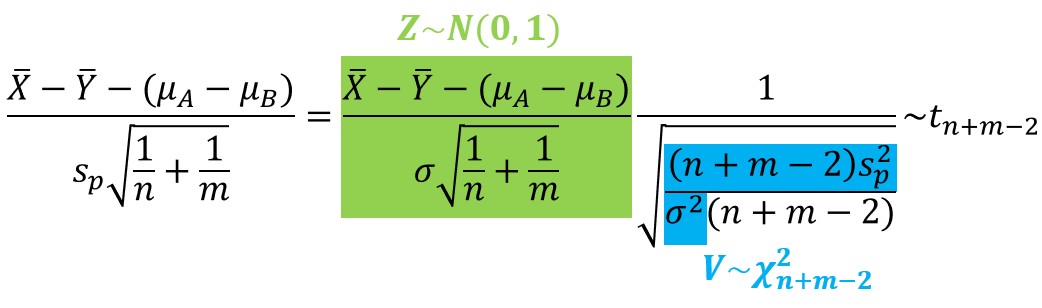
따라서 point estimator는 자유도가 $(n+m-2)$인 t-분포를 따른다.
$1-\alpha$ 신뢰구간을 구하면
\[ \mu_A - \mu_B \in \left( \bar{x}-\bar{y} \pm t_{\alpha/2, n+m-2} s_p \sqrt{\frac{1}{n} + \frac{1}{m}} \right) \]
Two-Sample z-Procedure
두 모분산 $\sigma_A^2$와 $\sigma_B^2$가 모두 알려져 있을때(known) 사용할 수 있다.
이때는 t-분포가 아니라 정규분포를 이용하므로 자유도라는 개념이 존재하지 않는다.
따라서 $1-\alpha$ 신뢰구간을 구하면
\[ \mu_A - \mu_B \in \left( \bar{x}-\bar{y} \pm z_{\alpha/2} \sqrt{\frac{\sigma_A^2}{n} + \frac{\sigma_B^2}{m}} \right) \]
two-sided p-value = $2 \times \Phi(-|z|)$
one-sided p-value = $1-\Phi(z)$ 또는 $\Phi(z)$



