t-intervals vs. z-intervals
모평균(population mean)을 추정할 때 모평균과 모분산을 모두 모를때(both unknown) t-procedure를 이용한다.
정리하자면 다음과 같은 상황에서 모평균을 추정할 때 t-procedure를 사용한다.
- population이 normal distribution임이 알려져 있다. (매우 강력한 가정!)
- $\mu$와 $\sigma^2$가 알려져 있지 않다. (both unknown)
- sample size $n$은 사실 상관이 없다.
※ CLT에 의해 $n \ge 30$인 경우에도 사용한다고 하지만, 이 경우 t-procedure보다 z-procedure를 사용하는 것이 옳다.
※ $n \ge 30$인 경우에 $t$-procedure를 사용해도 문제는 없지만 굳이? 왜? $z$-procedure가 있는데?
Remark: Normal related statistics
확률변수 $X$가 정규분포 $N(\mu, \sigma^2)$를 따른다면(이 사실을 안다면) 다음의 성질을 만족한다.
- $\cfrac{\overline {X} - \mu}{\sigma / \sqrt{n}} \sim N(0, 1)$
- $\cfrac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1}$
- $\overline {X}$와 $S^2$는 독립이다.
- $\cfrac{\overline {X}-\mu}{S / \sqrt{n}} \sim T_{n-1}$
Introduction
모평균을 추정할 때 점추정이 좋은가 구간추정이 좋은가?\
예1) $X \sim \text{Poi}(\lambda)$의 parameter $\lambda$를 추정해보자.
MLE에 의해 $\hat{\lambda}=\bar{x}$임을 이용하자.
그렇다면 $P(\overline{X} = \lambda)$를 이용할 것인가? discrete하지만 $P(\overline{X} = \lambda) \approx 0$일 것이다.
예2) $X \sim N(\mu, \sigma^2)$에서 $\hat{\mu} = \bar{x}$임을 이용하면 $P(\overline{X} = \mu)=0$이다.
이렇듯 모평균을 추정할때 "모평균이 어떤 값일 확률"과 같은 표현은 적절하지 못하다.
대신에, "모평균이 어떤 구간에 있을 확률"과 같은 표현( $P(\mu \in [L, U]) = 0.95$ )을 사용하고 이 구간을 신뢰구간으로 한다.
$t$-Confidence Interval
이제 $X$가 정규분포를 따른다는 것을 안다고 하자. $X \sim N(\mu, \sigma^2)$ ($\mu, \sigma^2$ are both unknown)
$\cfrac{\overline{X} - \mu}{S / \sqrt{n}} \sim T_{n-1}$임을 이용하자.
$P\left( -t_{\alpha / 2, n-1} < \cfrac{\overline{X} - \mu}{S \ \sqrt{n}} < t_{\alpha/2, n-1} \right) = 1 - \alpha$ 이므로 $\mu$ 중심으로 다시 확률을 계산하면
\[ P\left(\overline{X} - t_{\alpha/2, n-1} \cfrac{S}{\sqrt{n}} < \mu < \overline{X} + t_{\alpha/2, n-1}\cfrac{S}{\sqrt{n}} \right) = 1-\alpha \]
위 $X$, $\overline{X}$, $S$는 확률변수이고, $\alpha$, $\mu$, $n$, $t_{\alpha/2, n-1}$, $s$은 숫자(number)이다.
우리가 얻은 데이터(observed/obtained values, data)에 따라 위 구간은 달라진다. 즉
\[ \mu \in \left[\bar{x} \pm t_{\alpha/2, n-1} \cfrac{s}{\sqrt{n}} \right] \]
이때 $t_{\alpha/2, n-1}$을 critival value(critical point)이라 하고, $\cfrac{s}{\sqrt{n}}$을 $\text{S.E.}(\hat{\mu})$이라 한다
Confidence Length
Confidence Length $L$ 역시 여기서 유도할 수 있다.
\[ L = 2 \times t_{\alpha/2, n-1} \cfrac{s}{\sqrt{n}} = 2 \times \text{(critical point)} \times \text{S.E.}(\hat{\mu}) \]
Effect of Sample Size
confidence length에서 우리는 특정 길이를 만족하는 $n$을 알 수 있다.
(같은 $\alpha$에서, confidence length가 짧을 수록 좋기 때문이다.)
confidence length가 $L_0$보다 길어지지 않도록(no larger than $L_0$) 하는 샘플 수는 다음과 같다.
\[ n \ge 4 \times \left( \cfrac{t_{\alpha/2, n-1}s}{L_0} \right)^2 \]
Additional Sampling
이미 먼저 pilot study로 $n_1$개의 샘플을 뽑아서 $s$를 계산하고 신뢰구간 $L$을 구했다고 하자. 즉
\[ L = \cfrac{2 t_{\alpha/2, n-1} s}{\sqrt{n_1}} \]
근데 신뢰구간을 줄이기 위해($L_0 > L$) 추가로 샘플을 추출해야한다고 하자. 이때
\[ n \ge 4 \times \left( \cfrac{t_{\alpha/2, n_1-1}s}{L_0} \right)^2 \]
을 계산하고, 추가로 뽑을 샘플 수는 $n - n_1$이다.
Example
첫번째 샘플 크기가 $n_1=60$이고 표본분산은 $s=0.134$, 99% 신뢰구간이 $[49.953, 50.045]$라 하자. 이때 신뢰구간의 길이는 $0.092$이다. 신뢰구간의 길이를 $0.08$이하로 만들기 위해서, 추가로 샘플링해야할 표본 수를 구해보자.
전체 샘플 크기는 $n \ge 4 \times \left( \frac{t_{0.005, 59} s}{L_0} \right)^2 = 4 \times (\frac{2.662 \times0.134}{0.08})^2=79.63$
따라서 전체 샘플 크기는 $80$이므로 추가로 필요한 샘플의 크기는 $80-60=20$이다.
Simulation and Confidence Interval
신뢰구간을 계산할 때, 우리는 주어진 데이터가 한번뿐이다. 그래서 95%의 신뢰구간이 와닿지 않을 수 있다.
만약에 $\bar{x}$를 계산할 수 있는 시뮬레이션이 반복된다면, 여러개의 신뢰구간을 얻을 수 있고, 이들 모든 구간에 모평균이 포함되는 것이 아니다.
모평균은 unknown일 뿐이지 어딘가에 고정된 값을 가지므로 다음과 같다.
Some Notations
확률변수는 대문자로, 실제 관측값은 소문자로 표기한다. 아래 tricky notation으로 살펴보면 다음과 같다.
(1) $P(\overline{X} \in [\overline{X} \pm t_{\alpha/2, n-1}\cdot \frac{S}{\sqrt{n}}]) = 1$
$\overline{X}$은 항상 구간 $[\overline{X} - k,\ \overline{X}+k]$에 포함되므로 확률값은 항상 $1$이다.
(2) $P(\mu \in [\overline{X} \pm t_{\alpha/2, n-1}\cdot \frac{S}{\sqrt{n}}]) = 1-\alpha$
(3) $P(\overline{X} \in [\overline{x} \pm t_{\alpha/2, n-1}\cdot \frac{s}{\sqrt{n}}]) = ?$
$\bar{x}$와 $s$는 실제 관측값이므로 확률변수가 아니라 어떤 고정된 값이다.
따라서 위 확률은 True라면 $1$이고 False라면 $0$이다. (depending on data $\bar{x}$)
(4) $P(\overline{X} \in [\mu \pm z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}}]) = 1-\alpha$
One-Sided Confidence Intervals
다음 두개의 사실을 remind하자
- $\cfrac{\sqrt{n}(\overline{X} - \mu)}{S} \sim t_{n-1}$
- $P\left( -t_{\alpha, n-1} \le \cfrac{\sqrt{n}(\overline{X} - \mu)}{S} \right) = 1 - \alpha$
따라서 confidence level이 $1-\alpha$이고 one-sided confidence interval (upper bound)은
\[ \mu \in \left(-\infty, \bar{x} + \cfrac{t_{\alpha, n-1} s}{\sqrt{n}} \right) \]
비슷하게, lower bound에 대한 confidence interval은
\[ \mu \in \left(\bar{x} - \cfrac{t_{\alpha, n-1} s}{\sqrt{n}}, \infty \right) \]
※ $t_{\alpha} < t_{\alpha/2}$이므로 one-sided가 two-sided보다 더 좁은(tight) boundary를 제공한다.
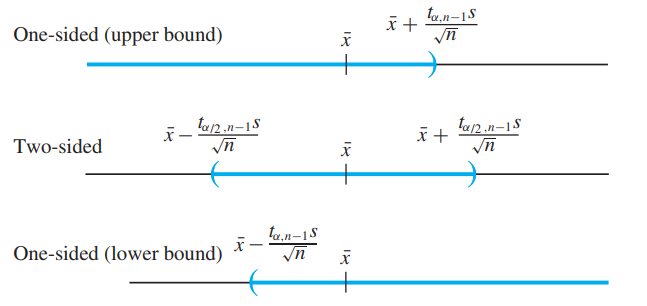
※ one-sided interval에서는 신뢰구간의 길이를 정의하지 않는다. upper/lower bound에 관심이 있는 경우이므로 confidence interval length는 고려대상이 아니다.
※ two-sided interval은 $t$분포의 대칭성을 이용하여 $t_{\alpha/2}$을, one-sided interval에서는 단측검정이므로 $t_{\alpha}$를 이용한다.
※ one-sided lower confidence interval은 upper bound를, one-sided upper confidence는 lower bound를 제공한다.
$z$-intervals
다음의 경우에는 $t$-procedure가 아니라 $z$-procedure를 이용하여 모평균을 추정한다.
- population distribution이 정확히 normal이고
- 모평균 $\mu$는 알려져 있지 않지만 모분산 $\sigma^2$는 알려져 있을 때
※ sample size $n$이 충분히 크면 LLN과 CLT에 의해 z-procedure로 근사(approximate)할 수 있다.
※ population distribution이 normal이면, 정확한 confidence interval을 구한다. (exact coverage, not approximation)
다음의 사실을 이용한다.
- $\cfrac{\overline{X} - \mu}{\sigma / \sqrt{n}} \sim N(0, 1)$
- $P(Z > z_{\alpha}) = \alpha$
따라서 two-sided confidence interval은 다음과 같다,
\[ \mu \in \left( \bar{x} - z_{\alpha/2} \cfrac{\sigma}{\sqrt{n}},\ \bar{x} + z_{\alpha/2} \cfrac{\sigma}{\sqrt{n}} \right) \]
one-sided interval은 다음과 같다.
\[ \mu \in \left( -\infty, \bar{x} + z_{\alpha}\cfrac{\sigma}{\sqrt{n}} \right) \text{ and } \mu \in \left(\bar{x} - z_{\alpha}\cfrac{\sigma}{\sqrt{n}},\ \infty \right) \]
Summary
- 데이터가 normality를 만족할 때,
- $\sigma$가 known이면 z-procedure
- $\sigma$가 unknown이면 t-procedure
- 데이터가 normality를 만족하지 않을 때,
- sample size $n$이 충분히 크면 z-procedure (이때 정확한 coverage가 아니라 approximation이다)
- 충분히 큰 sample size는 이론상 20~30이지만, 통계학과 교수님께서는 실제로는 50 이상은 되어야 한다고 한다.
