[Community Detection] Girvan-Newman (GN) Algorithm

 

Girvan-Newman: Divisive hierarchical clustering based on edge betweenness

Community Detection

우리는 그래프(네트워크)를 여러개의 모듈, 클러스터, 커뮤니티의 집합체로 생각한다.

Networks and Communities; Movies-to-Actors graph (Stanford CS246, MMDS)

graph를 partitioning하여 micro-market을 찾을 수 있다.

Find micro-markets by partitioning the query-to-advertier graph (Stanford CS246, MMDS)

 

소셜네트워크에서는 서로 겹치는(overlapping) social circle 혹은 circles of trust를 찾을 수 있다.

Twitter & Facebook (Stanford CS246, MMDS)

 

여기서는 undirected & unweighted network에서의 community detection에 알아보자.

Community Detection for Undirected Networks (Stanford CS246, MMDS)

 

Edge betweenness

해당 edge를 통과하는 최단거리의 개수 (Number of shortest paths passing through the edge)

(edge betweenness는 edge strength와는 다르다.)

 

Example of edge betweenness (MMDS)

 

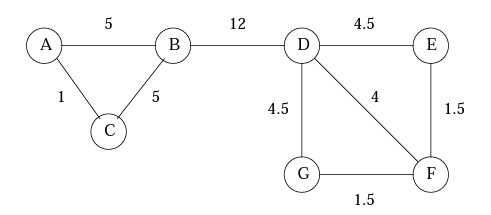
위 그림에서 몇가지 edge를 예를 들어보자.

$(B, D)$는 $\{ A, B, C \}$중 하나와 $\{ D, E, F, G \}$중 하나의 shortest path를 항상 지나가므로 $3 \times 4 = 12$이다.

$(E, F)$는 path $E \to F$, $E \to G$에 속한다. 근데 path $E \to G$는 $EFG$, $EDG$ 2개가 있으므로 $1/2$의 가중치를 갖는다. 따라서 $(E, F)$의 edge betweenness는 $1.5$이다.

 

[Computing edge betweenness]

Step 1: root 노드로부터 BFS를 통해 shortedt path를 찾는다. 같은 level에 있는 노드끼리의 edge는 절대로 root의 shortest path의 경로가 되지 않는다.

BFS starting from A (Stanford CS246, MMDS)

 

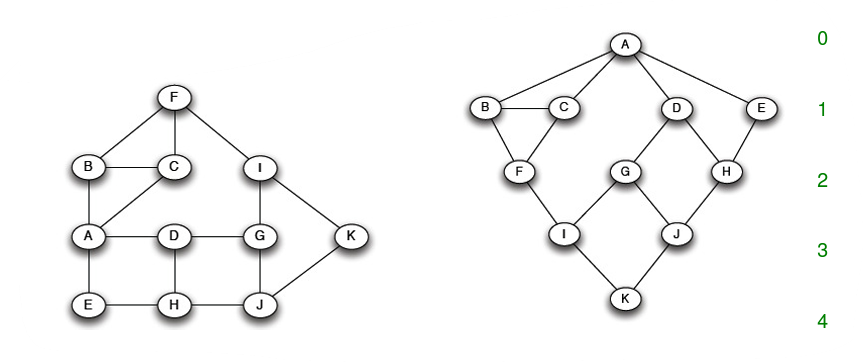
Step 2: 각 노드에는 root로부터 자기까지의 shortest path의 개수를 labeling한다. root 노드를 1로 표기하고, child node는 parent node의 label의 합으로 표기한다.

Count the number of shortest paths from root to all other nodes (MMDS)

 

 

Step 3: 이제 각 edge에 labeling을 할 차례이다. (bottom에서부터) 각 edge $e$는 root로부터 해당 노드로 가는 shortest path의 비율을 기록한다. bottom level의 노드는 1이고 연결된 edge는 노드의 합이다. 만일 어떤 노드의 값이 $x$이고 연결된 edge가 $n$개라면 각 연결된 edge는 $x/n$의 값을 갖는다. 

맨 처음 $K$는 $1$의 node flow 값을 갖고, 연결된 parent의 최단경로의 개수가 각각 3개, 3개이므로 동등하고 $1$을 $3:3=1:1$의 비율로 나누면 $0.5,\ 0.5$의 betweenness를 갖는다.

$J$ 노드의 node flow는 $1$과 $K$와 연결된 betweenness 값을 합하여 $1.5$의 값을 가진다. $J$의 parent는 $G$와 $H$이고, 이들의 shortest path의 개수의 비율은 $1:2$이므로 $J$의 node flow 값($1.5$)을 $1:2$의 비율로 나누면 $0.5$, $1$의 betwenness를 얻는다.

 

 

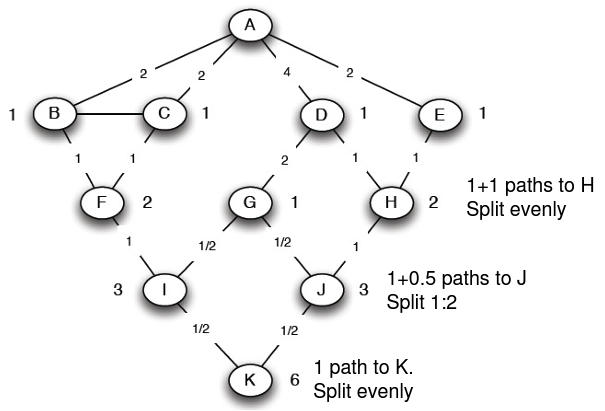
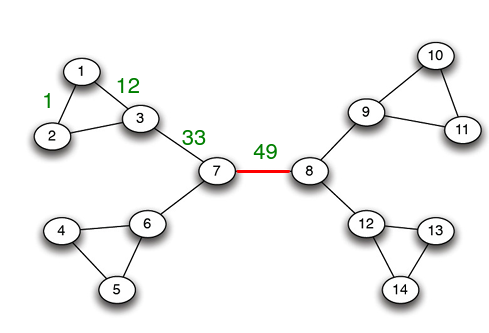
Step 4: 모든 노드에 대하여 root일 때 위의 Step 1~3을 반복하여 edge betwenness를 구한다. 마지막으로 각 edge마다 값을 더한 후 2로 나눈다. (every shortest path will be discovered twice)

 

Girvan-Newman: Algorithm

남아있는 edge가 없을 때까지 다음을 반복한다

• edge betweenness를 계산한다. (매 반복할 때 마다 새로 계산해야한다)
• 가장 높은 betweenness를 가지는 edge를 제거한다.

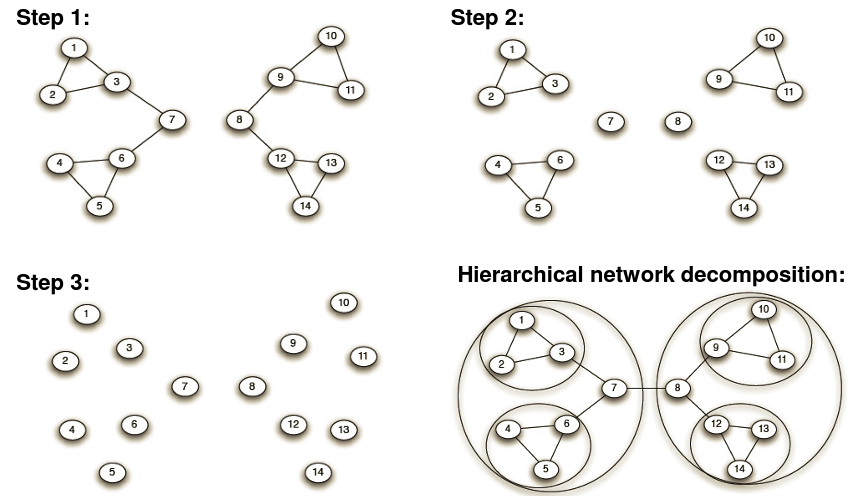
connected component는 community를 형성하고, GN-알고리즘을 이용하면 Network의 hierarchical decomposition 역시 얻을 수 있다.

 

Example: Girvan-Newman Algorithm (Stanford CS246, MMDS)

 

Modularity ($Q$)

Definition: Network가 community로 얼마나 잘 나눠져있는가(partitioned)에 대한 measure이다.

직관적으로 생각해보면 modularity $Q$는 다음에 비례할 것이다.

partition 집합을 $S$라 하고 그 원소를 $s$라 하면 다음과 같다.

\[ Q \propto \sum_{s \in S} [\text{(# edges within group }s) - \text{(expected # edges within group }s)] \]

 

edge 개수의 기댓값을 계산해야하므로 Null model을 도입한다.

node degree가 주어졌을 때, random하게 연결되었다고 생각하여 edge 개수의 기댓값을 구해보자.

두 노드 $i$와 $j$의 degree를 각각 $k_i$, $k_j$라 하고 전체 edge개수를$m$이라 하면

\begin{align} \text{expected # edges} &= \cfrac{1}{2} \sum_{i \in N} \sum_{j \in N} \cfrac{k_i k_j}{2m} \\ &= \cfrac{1}{2} \cdot \cfrac{1}{2m} \bigg( \sum_{i \in N} k_i \bigg) \bigg( \sum_{j \in N}k_j \bigg) \\ &= \cfrac{1}{4m} (2m) (2m) \ (\because \sum_{u \in N}k_u=2m) \\ &= m \end{align}

 

따라서 그래프 $G$와 partitioning $S$가 주어졌을 때의 modularity $Q$는 다음과 같다.

\[ Q(G,S) = \cfrac{1}{2m} \sum_{s \in S} \sum_{i \in s} \sum_{j \in s} \bigg( A_{ij} - \cfrac{k_i k_j}{2m} \bigg) \]

 

$Q \in [-1, 1]$의 범위를 갖는다. $Q$의 범위가 $0.3 \~ 0.7$이면 significant community structure를 갖는다고 한다. $Q=0$이면 어떠한 패턴도 없으며, $Q$가 $-1$에 가까우면 anti-community이다.

 

Modularity: Number of clusters (Stanford CS246, MMDS)