Random Forests
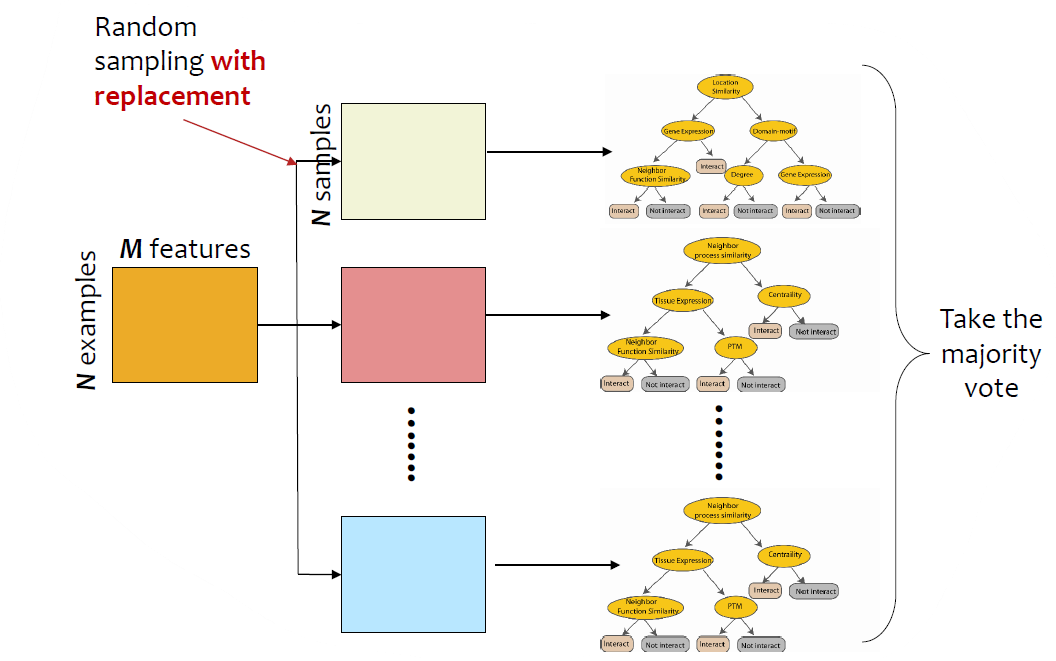
Random Forests는 Bagging algorithm의 대표적인 방법이다.
전체 데이터가 $N \times M$ 행렬이라 하자. ($N$은 instance 개수, $M$은 feature 개수)
그리고 복원추출(random sampleing with replacement)을 이용하여 $N$개의 sample을 추출하여 학습데이터셋을 만든다.
각 복원추출된 데이터 $D_i$마다 decision tree $C_i$를 학습한다.
(각 모델이 사용하는 feature 수는 아래 Training을 참고)
Note: Regression에서는 averaging, Classification에서는 max-voting을 이용한다.
Bootstrap Sample
$\mathcal{D} = \{ X_1, \dots, X_n \}$ 에서 sample size가 $n$이고 복원추출한 표본을 bootstrap sample이라 한다.
bootstrap sample에는 어떤 $X_i$는 여러번 등장할 수 있고 어떤 $X_j$는 한개도 없을 수 있다.
각 $X_i$는 한번도 선택되지 않을 확률이 $\left( 1 - \frac{1}{n} \right)^n$ 이다.
따라서 $n$이 커지면 $\left( 1 - \frac{1}{n} \right)^n \approx e^{-1} = 0.368$
따라서 우리는 $\mathcal{D}$의 63.2%의 데이터는 최소 한번 bootstrap sample에 있을 것으로 기대된다.

Training
각 tree(혹은 classifier)는 (복원추출로 얻은) 크기가 $N$인 sample을 training set으로 한다. (original data는 $\mathcal{D}$라 하고, training set은 $D_i$라 하자.) 이때 약 63%의 training instance가 샘플링될 것이라고 기대된다.
$M$개의 input variable 중에서 $m$개의 변수만 랜덤하게 선택하여 노드를 split하는데 사용된다. ($m \ll M$)
즉 $m$개의 변수는 input variable의 부분집합이다.
$m$의 값은 상수로 고정된다.
각 tree는 pruning 없이 최대한 성장한다.
The forest error rate
forest의 error는 2가지 요인에 의해 달라진다.
correlation
forest의 두개의 tree의 correlation이 크면 forest error rate가 증가한다.
strength
각 tree의 strength가 강하면 forest error rate는 감소한다.
$m$의 값이 작아지면 correlation과 strength 모두 작아진다. OOB error rate를 이용하여 적절한 $m$의 값을 찾을 수 있다.
Out-of-Bag (OOB) Error Estimation
아래의 이유로, cross-validation이나 test set을 나눌 필요는 없다.
약 37%(1/3)은 bootstrap sample에 포함되지 않는데 이것을 out-of bag (oob) instance라고 부른다.
그래서 oob를 따로 testset으로 간주한다.

4개의 instance에 대하여 decision tree를 학습한다고 하자. 이때 $D_i$로 학습한 트리를 $DT_i$라고 하자.
$DT_1$의 training set은 녹색박스, OOB는 빨간색 박스라고 하자. 그렇다면 OOB는 $DT_1$에게 unseen data이므로 test set으로 간주할 수 있다. $DT_1$이 저 OOB를 YES라고 예측했다고 하자.
5번의 bootstrap을 통해 $DT_1, DT_3, DT_5$은 저 빨간 인스턴스가 OOB여서($DT_2, DT_4$는 bootstrap sample에 마지막 row가 있음) 각각 yes, no, yes라고 예측했다고 하자. 그렇다면 majority vote를 통해 yes로 예측할 것이다. 이 경우 OOB-error가 없다.

마찬가지로, 각 OOB sample은 $DT$들 중에서 자신을 포함하지 않는 $DT$를 모두 pass한 후 majority vote를 수행하여 정확하게 분류된 점수를 OOB score라고 한다.
Variable Importance
OOB data의 변수들을 랜덤하게 permute하여 모델의 성능을 비교한다.
(untouched oob data에서 correct class한 vote 수) - (permuted oob data에서 correct class한 vote 수)
만일 variable이 중요하지 않다면, variable의 순서를 바꿔도 위 계산식이 크게 다르지 않을 것이다.
중요한 variable일 수록 위 식의 값의 차이가 더 클 것이다.
forest 안의 모든 tree의 raw importance score의 평균값을 구하고, 표준편차로 나누어서 z-score를 구한다.

'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| [Ensemble] AdaBoost (0) | 2023.05.16 |
|---|---|
| [Ensemble] Random Forests in Python (scikit-learn) (0) | 2023.05.13 |
| [Ensemble] Basic Concept of Ensemble Methods, Bagging, Boosting (0) | 2023.05.12 |
| [Machine Learning] SVM in Python (2) - Margin, Regularization, Non-linear SVM, Kernel (0) | 2023.05.11 |
| [Machine Learning] SVM in Python (1) Decision Boundary (0) | 2023.05.10 |



