Transaction Data Setup
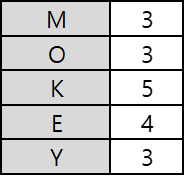
5개의 거래가 있는 아래 데이터에 대하여, min_sup=60%, min_conf=80%라 하자.

전체 transaction data가 5개이므로, min_sup 60% = 3개이다.
(1) Apriori
먼저 1-frequent itemset을 만들고 min_sup=3이 안되는 아이템을 지워 ($L_1$)을 만들자

$L_1$으로 self-join을 하여(임시 $C_2$)를 구한다.
그리고 $L_1$에 없는 아이템이 있다면(이 경우에는 없다) 그 후보는 pruning하여 $C_2$를 구한다.

이렇게 구한 $C_2$ 중에서 min_sup=3 이상이 되는 itemset만 남겨 $L_2$를 만든다.

$L_2$를 self-join을 하면 다음과 같다.

그런데 {M, O, K}의 경우, subset {M, O}는 $L_2$에 없다. 따라서 prunning한다.
{M, O, E}의 경우, subset {M, O}는 $L_2$에 없다. 따라서 prunning한다.
{M, K, E}의 경우, subset {M, E}는 $L_2$에 없다. 따라서 prunning한다.
{M, K, Y}의 경우, subset {M, Y}는 $L_2$에 없다. 따라서 prunning한다.
{O, K, Y}의 경우, subset {O, Y}는 $L_2$에 없다. 따라서 prunning한다.
{K, E, Y}의 경우, subset {K, Y}는 $L_2$에 없다. 따라서 prunning한다.
따라서 $C_3$ = {OKE}만 남는다. 그리고 $C_3$의 모든 원소(1개이지만)는 $\mathcal{T}$에 3개 존재하고 min_sup 조건도 만족한다. 따라서 $L3$역시 {OKE}이다.
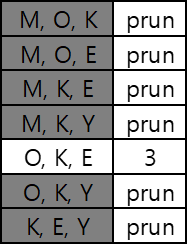
$L_3$을 self-join해도 $L_4 = \emptyset$이 된다. 따라서 apriori 알고리즘은 여기서 멈춘다.
따라서 apriori 알고리즘으로 얻은 모든 frequent itemset은 다음과 같다.
{M, O, K, E, Y, MK, OK, OE, KE, KE, OKE}
(2) FP-growth Tree
우선 각 아이템마다 빈도수를 구하고, min_sup이 60%(3개) 미만인 아이템은 제외한다.
이렇게 얻은 frequent item을 빈도수가 많은 순서로 정렬하면 다음과 같다.
같은 빈도에 대하여 순서는 상관없지만, 편의상 알파벳순으로 하자.
\[ \{ K:5, \ E:4,\ M:3,\ O:3,\ Y:3 \} \]
이렇게 얻은 빈도수 대로 f-list를 재구성하자.

이제 T100부터 차례대로 FP-Tree를 만든다.

CPB(item): item의 Conditional Pattern Based
CFPT(item): item의 Conditional FP-Tree
FP: Frequent Pattern
이라 하자.
CPB(Y) = { <K, E, M, O>: 1, <K, E, O>: 1, <K, M>:1 }
CFPT(Y) = { K:3 } (E:2, M:1, O:2 는 min_up 미만이므로 탈락된다.)
FP = { KY:3 }
CPB(O) = { <K, E, M>: 1, <K, E>: 2 }
CFPT(O) = { K, E: 3 }
FP = { K, O 3, E, O: 3, K, E, O: 3}
CPB(M) = { <K, E>: 2, <K>: 1 }
CFPT(M) = { <K>: 3 }
FP = { K, M:3 }
CBP(E) = { <K>: 4 }
CFPT(E) = { <K>: 4 }
FP(E) = { K,E: 4 }
따라서 FP-growth 알고리즘으로 얻은 frequent itemset은 다음과 같다.
(당연히 apriori의 결과와 동일하다.)
{K:5, E:4, M:3, O:3, Y:3, KY:3, KO: 3, EO:3, KEO:3, KM: 3, KE: 4}
Rule generation
위 두가지 방법으로 frequent-itemset을 구했다.
\[ \{M, O, K, E, Y, MK, OK, OE, KE, KE, OKE\} \]
다음을 만족하는 rule을 찾아보자. (단, $s=60\%, c=80\%$)
\[ \forall x \in \mathcal{T}, buys(X, item_1) \wedge buys(X, item_2) \Rightarrow buys(X, item_3) \quad [s, c] \]
$buys(X, E) \wedge buys(X, O) \Rightarrow buys(X, K) \quad [60\%, 100\%]$
$buys(X, K) \wedge buys(X, O) \Rightarrow buys(X, E) \quad [60\%, 100\%]$
'스터디 > 데이터사이언스' 카테고리의 다른 글
| [Data Science] Missing Values (0) | 2023.04.21 |
|---|---|
| [Data Science] Chi-square test. 카이제곱검정 (0) | 2023.04.20 |
| [Data Science] Decision Tree - GINI index와 CART 알고리즘 (0) | 2023.04.16 |
| [Data Science] The classification and decision tree (0) | 2023.04.15 |
| Entropy의 의미 (정보이론) (0) | 2023.04.14 |



