상관 계수
한국어 위키백과) 두 변수 사이의 통계적 관계를 표현하기 위해 상관관계의 정도를 수치적으로 나타낸 계수.
여러 유형의 상관 계수가 존재하고, 모두 $[-1, 1]$의 범위를 갖는다. $\pm 1$은 강한 상관성을, $0$은 상관성이 없다는 뜻이다.
가장 중요한 유의점으로, 상관계수가 큰 것이 인과관계를 나타내지 않는다. (인과 관계를 알아내기 위해서는 보다 복잡한 과정이 필요하다. 추후 설명할 예정)
Pearson's r, PCC(Pearson's Correlation Coefficient)
두 확률변수 $X, Y$에 대하여 선형적(linear) 상관관계를 측정한다.
모집단(population)을 알 때의 상관계수와 표본에서의 상관계수의 정의가 다르다.
우선, 모집단 상관계수는
\[ \rho_{X, Y} = \cfrac{\text{Cov}(X, Y)}{\sigma_X \sigma_Y} \]
표본 상관계수는
\[ r_{xy} = \cfrac{\sum_{i=1}^{n}(x_i - \bar{x}_i)(y_i - \bar{y}_i) }{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x}_i)^2} \sqrt{\sum_{i=1}^{n}(y_i - \bar{y}_i)^2}} = \cfrac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{(n-1)s_x s_y} \]
$n$은 표본 수, $\bar{x}, \bar{y}$는 $x, y$의 표본 평균, $s_x, x_y$는 $x, y$의 표본표준편자이다.
피어슨 상관계수는 두가지를 가정하는 경우에 의미가 크다.
- 두 변수는 서로 선형관계이다.
- 정규분포를 따른다.
데이터가 점수(score, 별점, 평점 등)인 경우, 이상치(outlier)나 극단값(extreme value)이 존재하기 때문에 피어슨 상관계수적절하지 않다. 이러한 경우, 순위(rank) 정보가 유의미한 정보를 줄 수 있다.
Spearman's rho
\[ \rho = 1 - 6\cfrac{\sum_{i=1}^{n}(r(x_i) - r(y_i))^2}{n(n^2-1)} = 1 - 6\cfrac{\sum_{i=1}^{n}d_i^2}{n(n^2 - 1)} \]
$r(x_i)$는 $X=[x_1, \dots, x_n]$를 오름차순으로 정렬하여 $x_i$의 순위(rank)를 의미한다.
$d_i = r(x_i) - r(y_i)$, 두 랭크의 차이이다. (절댓값이 없지만 제곱을 하므로 상관이 없다.)
데이터에 따라 rank가 같은 경우가 있을 수 있는데, 이 경우 그들의 rank의 평균을 이용한다. (아래 예시에서 설명)
rank correlation의 한 종류이다.
PCC는 선형적인 관계만 파악할 수 있지만, Spearman's rho를 이용하면 단조관계(monotonic relationship)를 파악할 수 있다. 따라서 PCC보다 outlier나 extreme value에 강하다.
Tied ranks
rank 값이 중복되어있는 경우에 같은 rank를 갖는 그룹끼리 평균값을 내서 계산한다.
예를 들어, 5등이 2명인 경우 각각 5등과 6등이 될 수 있으므로 둘의 평균인 5.5등을 rank로 한다.
하지만 스피어만 상관계수 역시 단조관계만 설명하므로, 또다른 비선형 관계(e.g. $y=x^2$)에서는 계수가 $0$일 수 있다.
Kendall's tau
\[ \tau = \cfrac{C-D}{C+D} = \cfrac{C-D}{\dbinom{n}{2}} \]
$C$는 concordant pair의 개수, $D$는 discordant pair의 개수
rank correlation의 한 종류이다.
https://en.wikipedia.org/wiki/Concordant_pair 에 따르면 concordant/discordant pair의 정의는
\[ \text{sgn}(X_i - X_j) = \text{sgn}(Y_i - Y_j) \ \text{(concordant)} \]
\[ \text{sgn}(X_i - X_j) = -\text{sgn}(Y_i - Y_j) \ \text{(discordant)} \]
Tied ranks
rank 값이 중복되어있는 경우에 $C, D$의 값이 다르므로 공식을 약간 변형하여 사용한다.
\[ \tau_b = \cfrac{C-D}{\sqrt{(n_0 - n_1)(n_0 - n_2)}} \]
$n_0 = \binom{n}{2} = \frac{n(n-1)}{2}$ (n_0 \neq C+D )
$n_1 = \sum_{i}\frac{t_i(t_i-1)}{2}$, $t_i$는 $i$번재 그룹에 있는 tied value의 개수
$n_2 = \sum_{i}\frac{t_i(t_i-1)}{2}$, $t_i$는 $i$번재 그룹에 있는 tied value의 개수
Examples
Python scipy 패키지의 라이브러리를 이용하여 간단히 계산할 수 있다.
scipy 라이브러리의 경우, tied value(rank 가 같은 경우)도 보정하는 식을 사용한다.
import numpy as np
import pandas as pd
from sklearn import datasets
import matplotlib.pyplot as plt
from scipy.stats import pearsonr
from scipy.stats import spearmanr
from scipy.stats import kendalltauExample 1: Linear with outliers
def generate_linear(n_samples, n_outliers=0):
x, y = datasets.make_regression(n_samples=n_samples, n_features=1, noise=10, random_state=42)
x, y = datasets.make_regression(n_samples=n_samples, n_features=1, noise=10, random_state=42)
x[:n_outliers] = 3 + 0.5 * np.random.normal(size=(n_outliers, 1))
y[:n_outliers] = -3 + 10 * np.random.normal(size=n_outliers)
x = np.ravel(x)
y = np.ravel(y)
return x, yx, y = generate_linear(40, 5)
plt.scatter(x, y)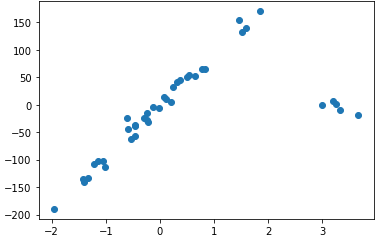
pcc, _ = pearsonr(x, y)
rho, _ = spearmanr(x, y)
tau, _ = kendalltau(x, y)
print(f'Pearson r : {pcc:.4f}') # 0.6179
print(f'Spearman rho : {rho:.4f}') # 0.8263
print(f'Kendall tau : {tau:.4f}') # 0.7026
Example 2: Non-linear but monotonic
def generate_rectifed(n_samples, r=0.5):
a, b = 2, 5
p = int(n_samples * r)
x = np.linspace(0, 5, n_samples)
y1 = a * x[:p] + np.random.normal(scale=0.5, size=len(x[:p]))
y2 = b * x[p:] * x[p:] - b * x[p] * x[p] + a * x[p] + np.random.normal(scale=2, size=len(x[p:]))
y = np.append(y1, y2)
return x, yx, y = generate_rectifed(50, r=0.5)
plt.scatter(x, y)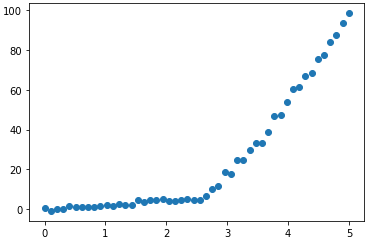
pcc, _ = pearsonr(x, y)
rho, _ = spearmanr(x, y)
tau, _ = kendalltau(x, y)
print(f'Pearson r : {pcc:.4f}') # 0.8916
print(f'Spearman rho : {rho:.4f}') # 0.9886
print(f'Kendall tau : {tau:.4f}') # 0.9380
'스터디 > 데이터사이언스' 카테고리의 다른 글
| [Data Science] Measuring Data Similarity and Dissimilarity (0) | 2023.03.22 |
|---|---|
| [Data Science] Data Preprocessing (1) - Overview (0) | 2023.03.21 |
| [Data Science] Basic Statistical Description of Data (0) | 2023.03.14 |
| [Data Science] Attribute Types (0) | 2023.03.09 |
| [pandas] [판다스] DataFrame 조작하기, MultiIndex (0) | 2023.02.15 |



