Linear Regression (선형회귀)

선형회귀를 푸는 3가지 방법을 소개한다.

1. 정규방정식(행렬)으로 풀기

2. sci-kit learn으로 풀기

3. Deep Neural Network으로 풀기 (Pytorch)

행렬식으로 표현하기

다음과 같은 linear model이 있다고 하자

$$Y = \beta_0 + \beta_1 x_1 + ... + \beta_k x_k + \epsilon$$

그리고 $n$개의 independent observation, $y_1, y_2, ..., y_n$이 있다고 하자.

우리는 이를 행렬로 표현할 수 있는데 다음과 같다.

선형회귀 데이터를 행렬로 표현할 수 있다.

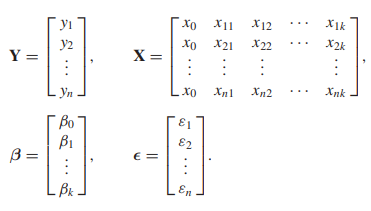
따라서 우리는

$$\mathbf{Y} = \mathbf{X \beta + \epsilon}$$

로 표현할 수 있다.

계수 $\beta$는 역행렬을 이용하여 구한다.

왼쪽에 $X^T$를 곱하면

$$\mathbf{X^TX \beta} = \mathbf{X^TY}$$

왼쪽의 $mathbf{X^YX}의 역행렬을 곱하면$

$$\mathbf{\beta} = \mathbf{(X^TX)^{-1}X^Ty}$$

 

Python 실습

1변수 선형회귀

다음과 같이 5개의 데이터가 있는 1변수 선형회귀를 구하자

1변수 선형회귀 데이터

실습1 풀이

예제1 파이썬 코드

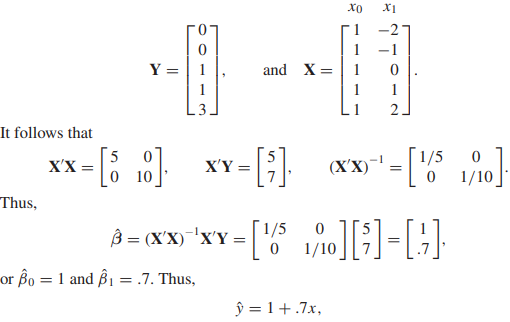
다변수 선형 회귀

Kaggle의 Fish market dataset을 이용하여 연습해보자.

https://www.kaggle.com/datasets/aungpyaeap/fish-market?datasetId=229906&sortBy=voteCount 

Fish market

데이터 읽고 살펴보기

7개의 물고기 종류가 있다.

피처간 분포를 보기 위해 pairplot으로 살펴보자.

sns.pairplot(data=df, kind='scatter', hue='Species', diag_kind='hist', corner=True)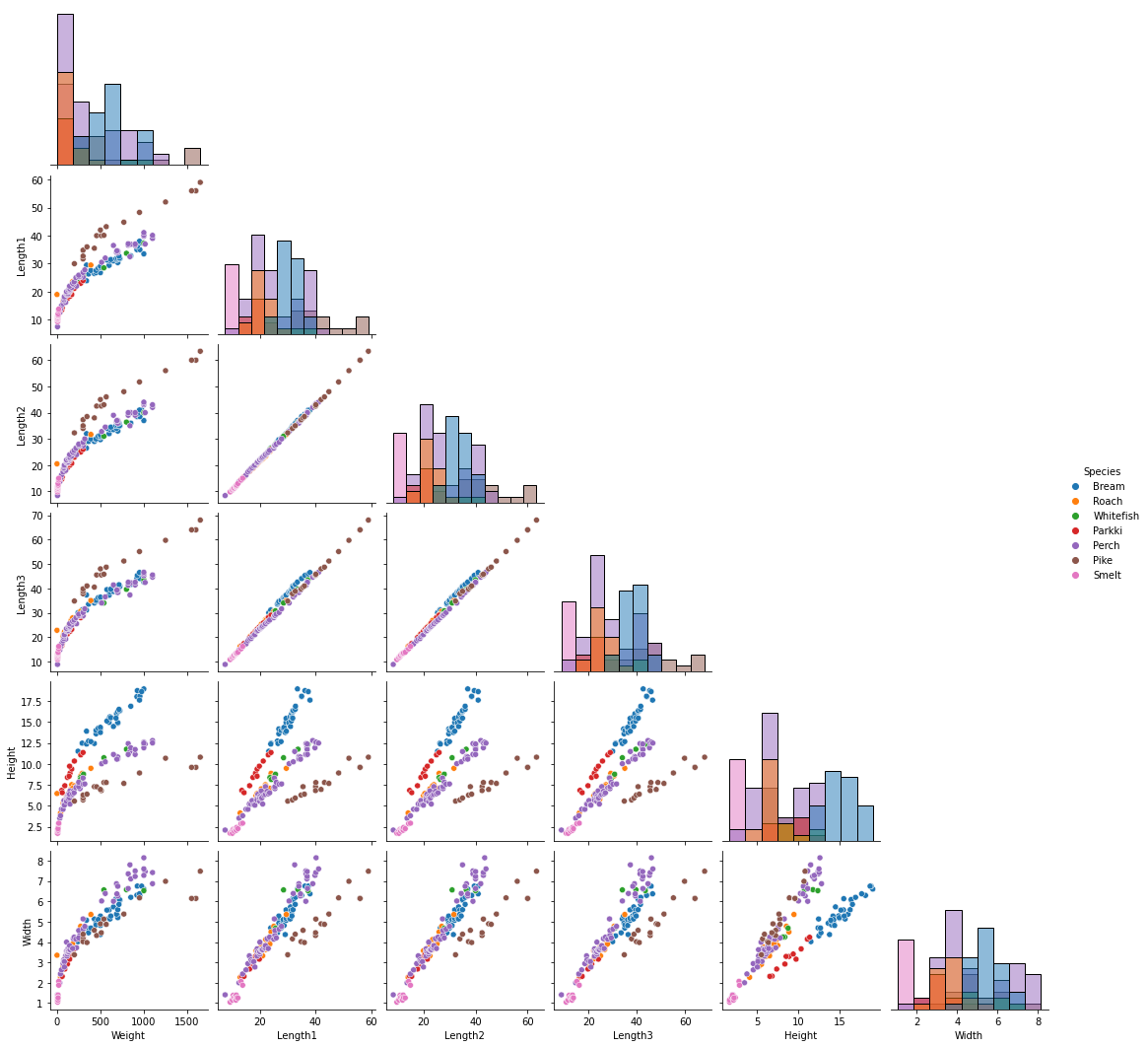

Weight는 5개 변수 Length1, Length2, Length3, Height, Width 모두 선형관계에 있음을 알 수 있다.

(plot의 첫번째 열을 보라)

대회가 아니다보니, 스스로 Weight를 예측하는 문제로 정의하고 시작하자.

 

$y$: Weight

$x_1$: Length1

$x_2$: Length2

$x_3$: Length3

$x_4$: Height

$x_5$: Width

$$y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + \beta_4 x_4 + \beta_5 x_5 + \epsilon$$

y = df['Weight']
X = df.iloc[:, 2:]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ---- 행렬 정규식을 이용한 풀이
# -- train set
X_train_np = X_train.to_numpy()
y_train_np = y_train.to_numpy()
ones = np.empty(X_train_np.shape[0])
ones.fill(1)
ones = ones.reshape(-1, 1)
X_train_np = np.append(ones, X_train_np, axis=1)

# -- test set
X_test_np = X_test.to_numpy()
ones_test = np.empty(X_test_np.shape[0])
ones_test.fill(1)
ones_test = ones_test.reshape(-1, 1)
X_test_np = np.append(ones_test, X_test_np, axis=1)

# -- solve by matrix
beta = solveLinearModel(y_train_np, X_train_np)
beta = beta.reshape(-1, 1)
y_pred_mat = np.matmul(X_test_np, beta)
y_pred_mat

다음은 사이킷런의 LinearRegression을 이용한 방법이다.

model = LinearRegression()
model.fit(X_train, y_train)
print(model.coef_, model.intercept_)
y_pred = model.predict(X_test)
print('MSE:', mean_squared_error(y_pred, y_test))
print('R2-score:', r2_score(y_pred, y_test))

이제 그 결과를 출력해보자

for feature in ['Length1', 'Length2', 'Length3', 'Height', 'Width']:
    plt.scatter(X_test[feature], y_test, label='true', color='b', alpha=0.5)
    plt.scatter(X_test[feature], y_pred, label='pred_sklearn', color='g', alpha=0.5)
    plt.scatter(X_test[feature], y_pred_mat, label='pred_matrix', color='r', alpha=0.5, marker='x')
    plt.xlabel(feature)
    plt.ylabel('Weight')
    
    plt.title(f'{feature}-Weight')
    plt.legend()
    plt.show()

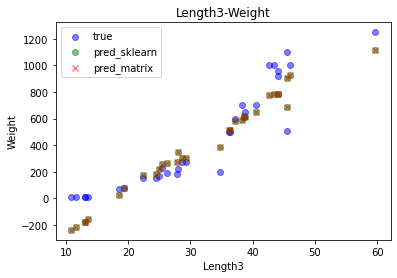
좌하단에 4개의 데이터 포인트는 Weight가 -200으로 음수를 예측한다. 그 외에는 괜찮은 것으로 보인다.

실제 데이터를 보면 Weight가 작은 데이터셋에서 완만한 곡선이 그려지는데, 이를 반영하지 못한 것으로 보인다.

 

Pytorch DNN으로 선형회귀 풀기

먼저 필요한 라이브러리를 import한다.

import numpy
import pandas

import matplotlib.pyplot as plt
import seaborn as sns

import torch
import torch.nn as nn

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

import os
os.environ['KMP_DUPLICATE_LIB_OK']='True'

3변수 선형회귀 데이터를 생성한다.

data_size = 10000
data = pandas.DataFrame({
    'x1': numpy.random.randn(data_size),
    'x2': numpy.random.randn(data_size),
    'x3': numpy.random.randn(data_size),
})
data['y'] = 5 * data['x1'] - 3 * data['x2'] + 2 * data['x3'] + 7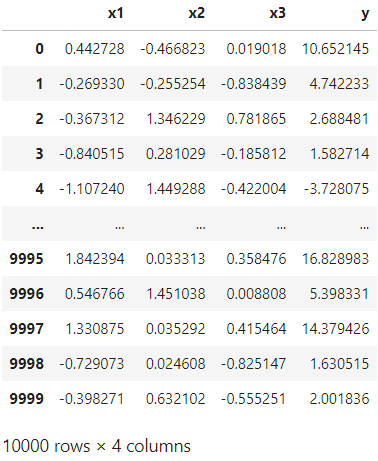

파이토치 모듈로 선형회귀를 해결하는 딥러닝 모델을 설계한다.

class LinearModel(nn.Module):
    def __init__(self, input_size, output_size):
        super().__init__()
        self.linear = nn.Linear(input_size, output_size, bias=True)
        
    def forward(self, x):
        return self.linear(x)

이제 모델을 학습하자.

파이토치는 torch.tensor만 계산할 수 있으므로, numpy로 생성된 데이터를 변환해야한다.

X_train, X_test, y_train, y_test = train_test_split(data[['x1', 'x2', 'x3']], data['y'], test_size=0.2, random_state=SEED)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)

N_EPOCH = 1000

model = LinearModel(3, 1)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
criterion = nn.MSELoss()

X_train_torch = torch.from_numpy(X_train.to_numpy()).float()
X_test_torch = torch.from_numpy(X_test.to_numpy()).float()
y_train_torch = torch.from_numpy(y_train.to_numpy()).reshape(-1, 1).float()
y_test_torch = torch.from_numpy(y_test.to_numpy()).reshape(-1, 1).float()

model.train()


for epoch in range(N_EPOCH):
    optimizer.zero_grad()

    outputs = model(X_train_torch)
    loss = criterion(outputs, y_train_torch)

    loss.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print(f'epoch: {epoch}, loss: {loss.item()}')

이제 테스트셋을 예측해보자

model.eval()
with torch.no_grad():
    pred_torch = model(X_test_torch)
print(pred_torch)

사이킷런이랑 결과를 비교해보자.

LR = LinearRegression()
LR.fit(X_train, y_train)
pred = LR.predict(X_test)
print(pred)

scatterplot으로 얼마나 잘 맞췄는지 보자.

plt.scatter(range(len(y_test)), y_test, color='b', s=10, label='true')
plt.scatter(range(len(y_test)), pred_torch, color='r', s=5, label='DNN')
plt.title('True-Predicted(DNN)')
plt.legend()
plt.show()

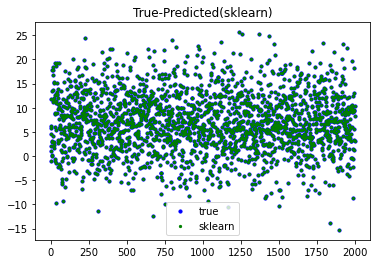
plt.scatter(range(len(y_test)), y_test, color='b', s=10, label='true')
plt.scatter(range(len(y_test)), pred, color='g', s=5, label='sklearn')
plt.title('True-Predicted(sklearn)')
plt.legend()
plt.show()