두 원 사이의 정수 쌍을 math 없이 풀어보자
- 문제 출처: 프로그래머스
- 난이도: level 2
- 참고: 없음
- input size: $1 \le r_1 < r_2 \le 10^6$
- (주관) 자료구조: 없음
- (주관) 알고리즘: 수학, 반복문
- (주관) 예상 시간복잡도: $O(r_1 + r_2)$ 또는 $O(r \sqrt{r})$
"질문하기"에도 다 math 모듈을 이용한 풀이가 힌트로 나와있었다.
원래 코딩테스트는 외부 라이브러리를 사용하지 못하기 때문에, 다른 방법을 찾아보았다.
"진짜 다른 의도는 없는데 이런게 어렵나여..?" 글을 참고하여 math 없이 풀수 있는 힌트를 얻었다.
자료형이 중요한 C/C++/java 에서도 overflow만 주의하면 충분히 정수형으로도 풀 수 있을 것 같다.
long long이 $2^{63}-1 \approx 2^3 \cdot (2^{10})^6 \approx 2^3 \cdot (10^{3})^6$이니까... 되지 않을까?

대칭성을 이용하면 1사분면 위의 점의 개수를 구하기만 하면 된다.
전체 점의 개수는 $4 \times \text{ (1사분면 위의 점) } + \text{ (축 위의 점 개수) }$ 이다.
STEP 1. 1사분면 위의 점들 찾기
1사분명 위의 점의 개수를 찾아보자.
단순히 2중 for-loop를 이용해 찾을 수 있다.
물론 이러면 $O(n^2)$이 되어 시간초과를 받는다.
대칭성을 이용해서 $y \ge x$ 영역의 점의 개수만 센다고 하더라도 시간복잡도는 변하지 않는다.
$x$의 값은 $1, 2, ..., r-1$일 때, $x^2 + y^2 \le r^2$를 만족하는 $y$의 (정수)최댓값을 구하면 곧 $y$의 개수가 된다.
$y_{min} = \bigg\lfloor \sqrt{r_1^2 - x^2} \bigg\rfloor$, $y_{max} = \bigg\lceil \sqrt{r_2^2 - x^2} \bigg\rceil$이니까, floor는 int()를 이용하고 ceil은 내가 직접 만들면 되는거 아닌가? (싱글벙글)
def ceil(x):
# Check if x is already an integer
if int(x) == x:
return int(x)
else:
return int(x) + 1
def solution(r1, r2):
answer = 0
for x in range(r2):
lower = ceil(((r1*r1) - (x*x)) ** (0.5))
upper = int(((r2*r2) - (x*x)) ** (0.5))
#print(x, lower, upper)
if lower == 0:
answer += upper - lower
else:
answer += upper - lower + 1
answer *= 4
return answer당연히 예제 테스트 케이스는 성공이다. 그러나 채점 테스트에서 런타임 에러가 났다.
수치 안정성이 너무 떨어지는 것 같다.
잠시 잊고 있었다. 컴퓨터의 부동소수점 연산은 매우 부정확하다는 것을...
그래서 소수 연산을 하고 싶으면 수치적으로 안정적인 넘파이 같은 모듈을 써야한다는 것을...
그러니까 ceil을 만들고 싶었으면 차라리 처음부터 math 모듈을 쓰는것이 나았다는 의미다.

STEP 2. 정수연산으로 방정식을 풀자.
($x$와 $r$이 고정일 때) $x^2 + y^2 \le r^2$을 만족하는 가장 큰 $y$를 찾는 것이 핵심이었다.
이는 예전에 약수 판정 코드를 배울때 알게된 건데, 루트연산을 이용하지 말고, 제곱을 해서 수학적으로 동일한 식을 정수연산으로 바꾸는 방법이다.
아래 코드는 $x^2 + y^2 \le r^2$를 만족하는 정수 점의 개수이다. (1사분면 한정, 축 위의 점 제외)
당연히 정직하게 2중 루프가 들어가기 때문에 $O(n^2)$가 되어 시간초과를 받는다.
def count_including_points_v0(r):
count = 0
for x in range(1, r):
for y in range(r, 0, -1):
if (x*x + y*y) <= r*r:
count += y
break
return count
def count_excluding_points_v0(r):
count = 0
for x in range(1, r):
for y in range(r, 0, -1):
if (x*x + y*y) < r*r:
count += y
break
return count
def solution(r1, r2):
answer = 0
count1 = count_excluding_points_v0(r1)
count2 = count_including_points_v0(r2)
answer = count2 - count1
# axis
answer += r2 - r1 + 1
# 4-ways
answer *= 4
return answer
STEP 3. 반복문 최적화
반복문을 보니 $x$가 증가하면 $y$의 값은 작아지지 않는가?
그런데 왜 굳이 $r$에서부터 상한을 잡고 $y$의 값을 찾을 필요는 없다.
$r-y_i$만큼의 탐색공간이 낭비되고 있다.
그리고 이는 $x_i$가 커질 수록 더 많이 낭비된다.
이전 단계에서 찾은 $y$에서 부터 상한을 잡아도 된다.
어차치 처음 만나는 정수만 찾으면 되니 시간복잡도는 $O(n)$에 유사하지 않을까 싶다.
(정확한 복잡도 유도는 못하겠다)

최종 코드는 다음과 같다.
def count_including_points(r):
count = 0
upper_bound = r
for x in range(1, r):
for y in range(upper_bound, 0, -1):
if (x*x + y*y) <= r*r:
count += y
upper_bound = y
break
return count
def count_excluding_points(r):
count = 0
upper_bound = r
for x in range(1, r):
for y in range(upper_bound, 0, -1):
if (x*x + y*y) < r*r:
count += y
upper_bound = y
break
return count
def solution(r1, r2):
answer = 0
count1 = count_excluding_points(r1)
count2 = count_including_points(r2)
answer = count2 - count1
# axis
answer += r2 - r1 + 1
# 4-ways
answer *= 4
return answer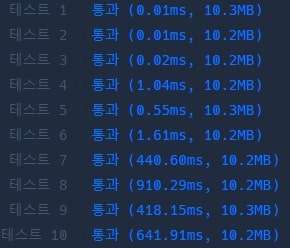
'스터디 > 알고리즘' 카테고리의 다른 글
| [Python] 퍼즐 조각 채우기 (0) | 2024.07.03 |
|---|---|
| [Python] 최고의 집합 (0) | 2024.07.02 |
| [Python] 도넛과 막대 그래프 (0) | 2024.06.17 |
| 시계열 데이터의 상관성 구하기 (time-series correlation) (0) | 2023.02.12 |
| [BOJ 6549] 히스토그램에서 가장 큰 직사각형 (0) | 2022.11.23 |



