Overfitting and Regularization
※ The blog post is based on lecture materials from Xavier Bresson, a professor at the National University of Singapore. The lecture materials can be found on the professor's LinkedIn. You can also found it at [1].
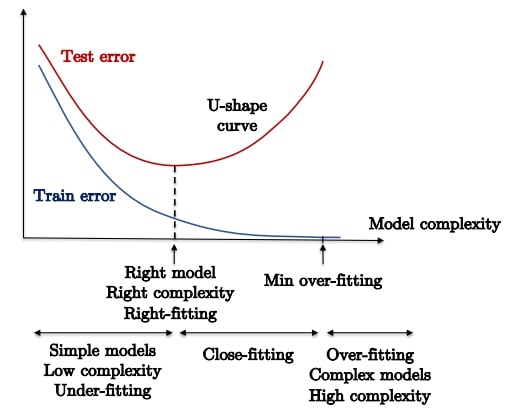
Under-fitting and over-fitting
- Underfitting
- learner가 충분한 표현력을 가지지 못함.
- training set에서 error를 생성.
- training/testing error 모두 높다.
- 방지 방법: learner의 expressivity(또는 complexity)를 증가시킨다.
- Overfitting
- learner가 지나치게 표현력을 가져서 training data에만 있는 패턴까지 학습함. (over-specialized of the training data)
- unseed data에 대하여 extrapolate가 불가능.
- training error는 작지만 test error는 높다.
- 방지 방법: loss regularization, cross-validation, early stopping, SGD, etc.
1. Loss regularizatioin
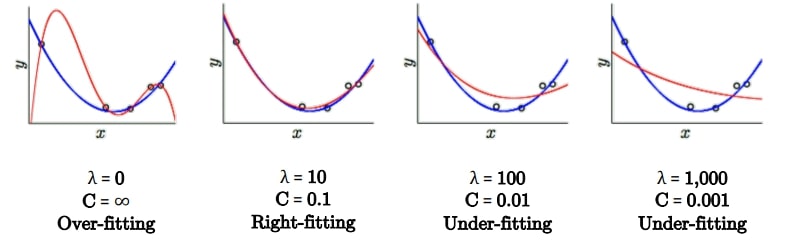
다음의 hypothesis space $\mathcal{H}_{10}$를 어떻게 $\mathcal{H}_{2}$로 줄일수 있을까?
$\mathcal{H}_2 = \{ f_{\theta}(x) = \theta_0 + \theta_1 x + \theta_2 x^2 \}$
$\mathcal{H}_{10} = \{ f_{\theta}(x) = \theta_0 + \theta_1 x + \theta_2 x^2 + \cdots + \theta_{10}x^{10} \}$

regresison에서 MSE optimization은 다음과 같이 정의된다.
\[ \underset{\theta}{\min}L_{\mathcal{H}}(\theta) \cfrac{1}{n} \sum_{i=1}^{n} \left( y^{(i)} - f_{\mathcal{H}}(x^{(i)}) \right)^2 \]
그러므로 $\mathcal{H}_{10}$의 최적화를 $\mathcal{H}_2$의 최적화와 동치시키려면 $\theta_3=\theta_4 = \cdots \theta_{10}=0$이라는 조건이 추가되어야 한다.
\[ \underset{\theta}{\min} L_{\mathcal{H}_{10}}(\theta) \text{ such that } \sum_{i \ge 3}^{d} \theta_i^2 \le C,\ C > 0 \]
$C$가 작으면 $\theta_{i \ge 3}$은 $0$에 가까워지므로 $\mathcal{H}_{10} = \mathcal{H}_2$이다.
$C$가 크면 $\theta_{i \ge 3}$은 $0$이 아닌 값을 가지게 된다.
이를 일반화한 loss regularization은 다음과 같다.
\[ \underset{\theta}{\min}L(\theta) \text{ such that } \sum_{j=0}^{d} \theta_j^2=\theta^T \theta \le C, \ C > 0 \quad \text{(1)}\]
또다른 방법은 lagrange multiplier를 이용한 식을 이용한다. (위 식과 동치이며, 풀기 더 쉽다)
\[ \underset{\theta}{\min}L(\theta) + \lambda \theta^T \theta, \ \lambda > 0 \quad \text{(2)} \]
(1)과 (2)가 동치가 되는 $C$와 $\lambda$가 존재하며, $C \propto 1/\lambda$의 관계를 갖는다.
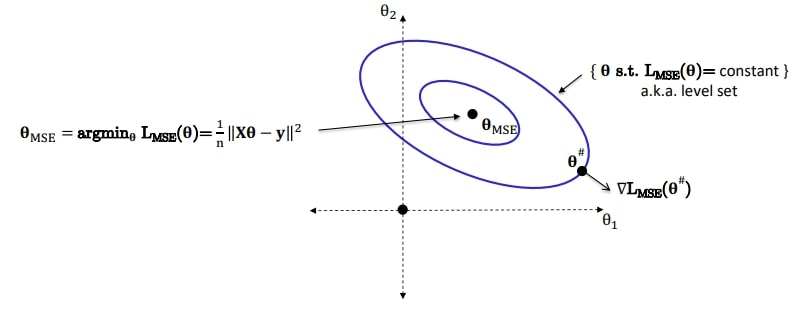
loss를 다음의 2개의 term으로 나누어서 생각해보자.
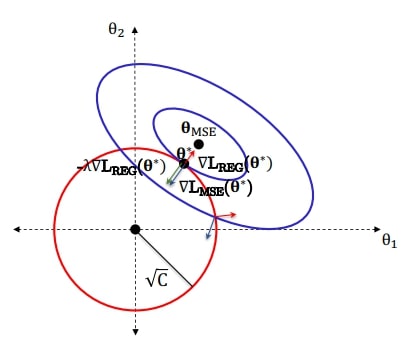
시각화를 위해, 2개의 파라미터를 갖는 MSE loss를 생각해보자. ($\theta = (\theta_1, \theta_2)$)
그리고 정규화 식은 $L_{reg}(\theta) = \theta^T \theta = \| \theta \| ^2$이므로 원점으로부터 $\sqrt{C}$만큼 멀어진 원의 형태가 된다.
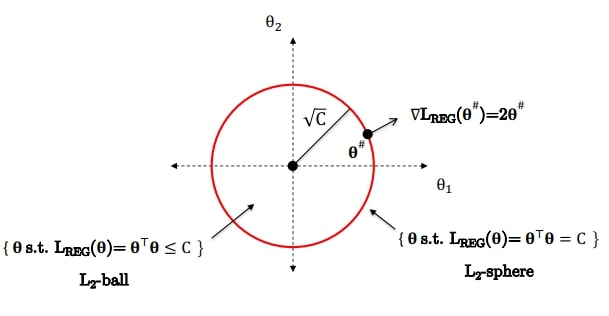
전체 loss의 최솟값을 갖는 파라미터를 $\theta^*$라 하면
\[ \theta^* = \underset{\theta}{\text{argmin}} L_{MSE}(\theta) + \lambda L_{REG}(\theta) \]
$\lambda$는 라그랑주 승수가 되어 두 loss가 접하는 곳의 $\theta$가 $\theta^*$가 된다.
위에서 사용된 정규화는 $L_2$이다. 이를 확장하여 $L_p$로 일반화할 수 있다.
- $L_2$ regularization (weight decay)
- 장점: strictly convex, 미분 가능, 빠른 최적화, robust
- 단점: $\theta_i$의 값이 작아지지만, 그래도 solution이 dense하다. 결국 모든 feature를 사용함
- $L_1$ regularization
- 장점: convex(not strictly), 빠른 최적화, robust, sparse solution이기 때문에 feature selection 가능
- 단점: 원점에서 미분 불가능
- $L_p$ regularization ($0 < p \le 1)$
- 장점: very sparse solution, $L_1$보다 강한 regularization
- 단점: not convex, non-differentiable, solution이 initial condition에 의존
- $L_p$ regularization ($p=\infty)$
- not stable, 실제로 거의 사용되지 않음
2. Cross-validation
위에서 설명한 loss regularization은 분명히 모델의 복잡도를 줄일 수 있다.
그러나 train 뿐만 아니라 test error를 최소화하는 올바른 $\lambda$를 찾아야 한다.
가장 간단한 방법은 training set을 2개로 나누어서 validation set을 만드는 것이다.
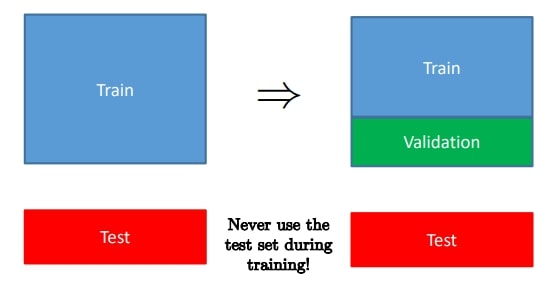
최적의 $\lambda$를 찾기 위해 $p$개의 $\lambda$를 후보라 하자. ($\lambda_1, \dots, \lambda_p$)
그리고 trainset에서 $\lambda$르르 이용하여 모델을 학습시키고, validation set에서 loss를 구한다.
가장 작은 loss를 갖는 $\lambda_j$가 $\lambda^*$가 된다.
수학적으로, $L_{val} = L_{test} \pm O\left( \frac{1}{\sqrt{m}} \right)$이다. ($m$은 validation set 크기, 증명은 [1] 참고)
작은 validation set은 test error의 좋은 estimator를 찾을 수 없다.
현대에는 big dataset을 갖는 경우가 많기 때문에, 작은 비율의 validation set으로도 test set의 분포를 충분이 근사할 수 있다.
그러나 과거 dataset, 혹은 비용 문제로 데이터를 모으기 어렵거나(핵융합 실험 데이터) 데이터가 보호되어 제한된 경우(의료 데이터)가 있다.
$n=1,000$과 같은 limited dataset에서는 위와 같은 방법을 사용할 수 없다.
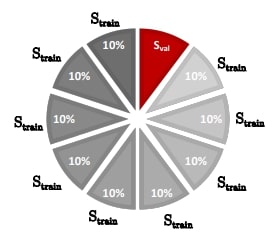
이러한 경우에는 k-fold cross-validation을 사용할 수 있다.
trainingset을 $k$개의 partition으로 나누어 각 fold는 약 $n/k$개의 data point를 갖게한다.
각 fold를 순회하면서, 나머지 $k-1$개의 fold는 train에 사용하고, 나머지 한 개의 fold는 validation set으로 사용한다.
3. Early stopping
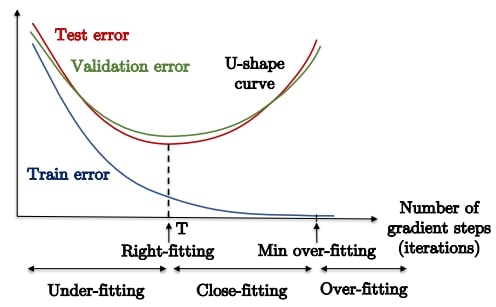
overfitting을 방지하는 가장 빠른 방법이다.
gradient step을 진행하면서 validation error가 증가하기 시작하면 최적화가 끝나지 않았어도 종료하는 방법이다.
수학적으로 최적화 이론에 부합하지는 않지만, 실제 학습 상황에서는 잘 동작한다.
특히 딥러닝을 학습할 때 자주 사용된다.
References
[1] lecture06_overfitting_regularization.pdf (storage.googleapis.com)
[2] Xavier Bresson — Teaching Resources (storage.googleapis.com)
'스터디 > 인공지능, 딥러닝, 머신러닝' 카테고리의 다른 글
| [Bayesian] Bayesian Linear Regression (베이지안 선형 회귀) (0) | 2024.05.08 |
|---|---|
| Double Descent: new approach of bias-variance trade-off (0) | 2024.03.03 |
| Gradients of Neural Networks (0) | 2023.11.27 |
| [Bayesian] Evidence lower bound (ELBO) and EM-algorithm (0) | 2023.11.11 |
| [CS224w, 2018] Network Representation (0) | 2023.10.17 |


