Spectral Clustering: Graph Cut with Eigenvectors
Graph Partitioning
다음과 같은 그래프 $G = (V, E)$에 대하여 우리는 2개의 disjoint group $\{ 1,2,3 \}$와 $\{ 4,5,6 \}$로 partitioning할 수 있다.

그렇다면 어떤게 좋은(good) partition으로 정의할 수 있을까? 어떻게 효율적(efficiently)으로 partition을 구할 수 있을까?
좋은 partition은 1) 같은 그룹끼리의 연결은 최대이며 2) 다른 그룹끼리의 연결은 최소화하는 것이다.
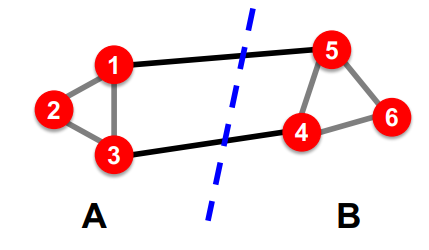
위 그림을 예시로 들면, 그룹 A, B 내부 노드끼리의 connection은 3개이고, A와 B의 connection은 2개이다.
Graph Cuts
partition의 "edge cut"을 함수의 형태로 표현할 필요가 있다. 여기서 Cut은 group내의 단 하나의 노드와 연결된 edge 집합이다. (set of edges with only one vertex in a group)
\[ cut(A, B) = \sum_{i \in A, j \in B}w_{ij} \]
참고로 weighted graph라면 $w_{ij}$는 weight이고, 그렇지 않다면 $w_{ij} = \{ 0, 1 \}$이다.
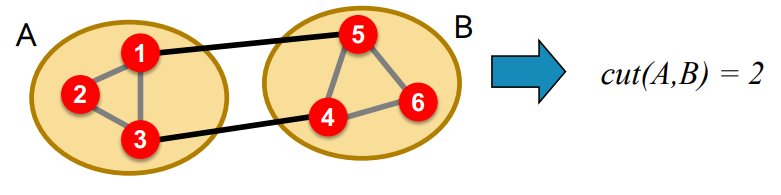
그렇다면 minimum-cut을 찾으면 된다.
\[ \underset{A,B}{\text{argmin }}cut(A,B)\]
Problem
1) 단순히 external cluster connection만 고려한다.
2) internal cluster connectivity를 고려하지 않는다.

Another Criterion: Conductance [Shi-Malik, 1997]
각 group의 상대적 밀도(relative to the density)를 기준으로 한다.
\[ \phi(A, B) = \cfrac{cut(A,B)}{\min (vol(A), vol(B))} \]
$vol(A) = \sum_{i \in A}k_i$: total weighted degree of the nodes in $A$
Problem: best conductane cut을 찾는 것은 NP-hard 이다.
Spectral Graph Partitioning
$G$의 adjacency matrix를 $A$라 하고 $x=(x_1, \dots, x_n) \in \mathbb{R}^n$이라 하자. $x$를 $G$의 노드의 label/value라고 간주하자. 그렇다면 $A\cdot x$는 무엇을 의미할까?
$y=Ax$라 하면 $y_i = \sum_{j=1}^{n} A_{ij}x_j = \sum_{(i,j) \in E}x_j$ 이므로 $y_i$는 $i$의 이웃노드들의 $x_j$의 합계와 동일하다. 이를 하나의 값으로 간주하면 $Ax = \lambda x$와 같이 쓸 수 있다.
Spectral Graph Theory
그래프의 eigenvectors $x^{(i)}$는 eigenvalue $\lambda_i$에 대응한다. $\Lambda = \{ \lambda_1, \dots, \lambda_n \}$
여기서는 $\lambda_1 \le \lambda_2 \le \dots \le \lambda_n$으로 정렬한다. ($\lambda_n$을 가장 큰 값으로 하자)
Example: d-regular graph
$G$의 모든 노드들의 degree가 $d$이고 $G$가 connected라 하자. (모든 노드끼리 연결되어있다.)
$x=(1, 1, \dots, 1)$이라 하면 $Ax = (d, d, \dots, d) = \lambda x$이므로 $\lambda = d$ 이다.
따라서 $A$의 가장 큰 고윳값은 $d$이다. (증명 생략)
Example: Graph on 2 components
$G$가 2개의 component를 가진다고 하자. 즉 각 component는 d-regular이다. component의 이름을 B, C라 하자.

$x'=(1, \dots, 1, 0, \dots, 0)$이라 하면 $Ax' = (d, \dots, d, 0, \dots, 0)$
$x''=(0, \dots, 0, 1, \dots, 1)$이라 하면 $Ax'' = (0, \dots, 0, d, \dots, d)$
두 component 모두 $\lambda=d$이다.

그래프가 오른쪽과 같다면 앞에서 살펴봤듯이 $x_n=(1, \dots, 1)$가 eigenvector이다.
그런데 eigenvector들은 서로 orthogonal하므로 $x_{n} \cdot x_{n-1}=0$
$x_{n-1}$은 노드들을 2개의 group으로 split하므로 $x_{n-1}[i] > 0$이거나 $x_{n-1}[i] < 0$이어야한다.
여기서 알 수 있는 것은 2nd largest eigenvalue가 C-group에 속하는 노드는 양수값을, B-group에 속하는 노드는 음수값을 갖게 한다.
Matrix Representations
$A$는 adjacency matrix이고 $D$는 degree matrix라 하자. 그러면 Laplacian matrix $L$를 다음과 같이 정의한다.
\[ L = D - A \]
$L$은 $n \times n$ symmetric matrix 임을 쉽게 보일 수 있다.
$L$의 trivial eigenpair는 $x=(1, \dots, 1)$, $\lambda_1=0$이다. ($Lx=0$이기 때문이다)
$L$의 eigenvalue는 non-negative real이고 eigenvector는 real & orthogonal 하다.
$\lambda_2$ of Laplacian Matrix
\[ \lambda_2 = \underset{x}{\min}\cfrac{x^\top Lx}{x^\top x} \]
$G$에서 $x^\top Lx$는 어떤 의미를 가지는가?
\begin{align} x^\top Lx &= \sum_{i,j = 1}^{n}L_{ij}x_i x_j \\ &= \sum_{i,j=1}^{n}(D_{ij} - A_{ij})x_i x_j \\ &= \sum_{i=1}^{n}D_{ii}x_i^2 - \sum_{(i,j) \in E} 2x_i x_j \\ &= \sum_{(i,j) \in E}(x_i^2 + x_j^2 -2x_i x_j) \\ &= \sum_{(i,j) \in E}(x_i - x_j)^2 \end{align}
우리는 $x$가 unit vector이고 $x$가 1st eigenvector와 orthogonal하다는 것을 알고 있다.
따라서 $\sum_i x_i^2=1$이고 $sum_i x_i \cdot 1 = \sum_i x_i = 0$ 이다.
Spectral Partitioning Algorithm
크게 3단계의 알고리즘으로 이루어져있다.
- Pre-processing
- 그래프 $G$의 Laplacian matrix $L$를 구한다.
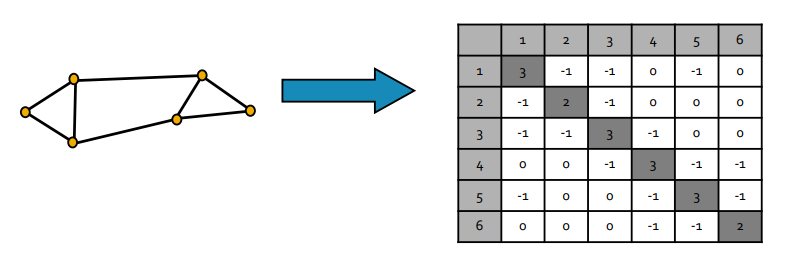
Preprocessing Step (Stanford CS224w, 2018)
- Decomposition
- $L$의 eigenvalue, eigenvector $\lambda$, $x$를 구한다.
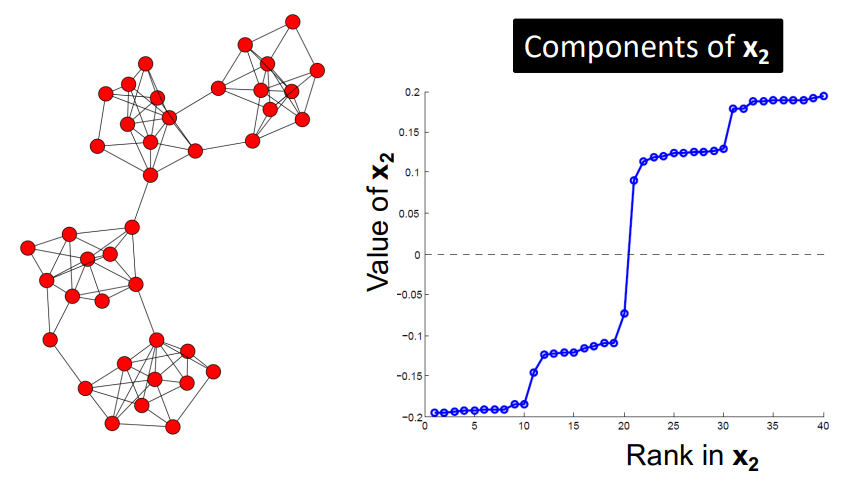
- (2nd smallest eigenvalue에 대응되는) $x_2$의 원소를 각 node에 대응시킨다.
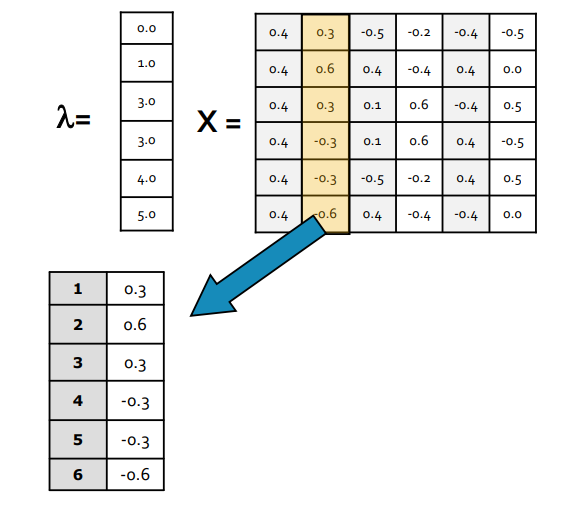
Decomposition Step (Stanford CS224w, 2018)
- Grouping
- component를 정렬한다
- sorted vector를 2개의 cluster로 나눈다.
- Method 1: $0$ 또는 median을 기준으로 두 클러스터로 구분한다.
- Method 2: minimize normalized cut을 구한다.

Example: Spectral Partitioning
아래는 2개의 파티션으로 나눠지는 그래프이다.

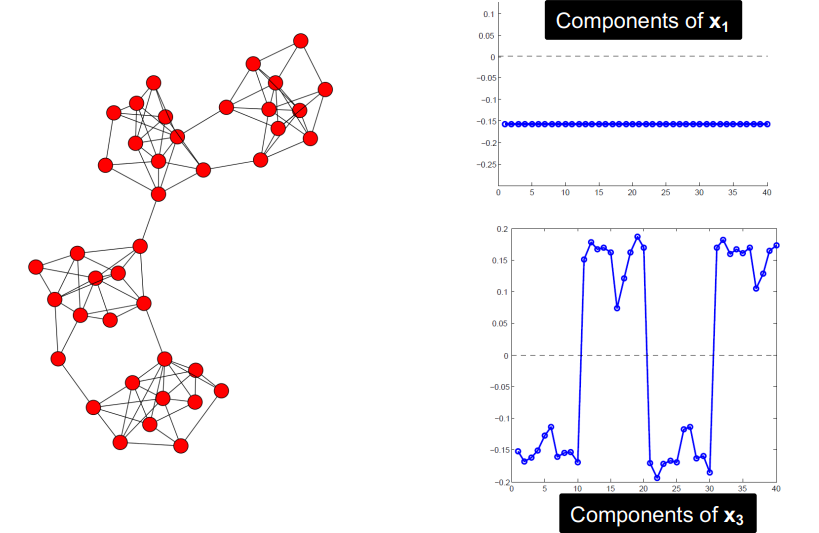
K-Way Spectral Clustering
spectral clustering은 2개의 cluster(partition)을 구하는 알고리즘이다. 그렇다면 $k$개의 클러스터로 구하는 방법은?
Recursive bi-partitioning [Hagen et al., 1992]
재귀적으로 bi-partitioning하여 hierarchical divisive manner로 접근한다.
단점: inefficient, unstable
Cluster multile eigenvectors [Shi-Malik, 2000]
multiple eigenvector로부터 reduced space를 구성한 후 k-mean 등의 알고리즘을 적용한다.
각 노드는 $k$개의 숫자로 표현되고(즉 $k$-dim 이다) clustering algorithm을 통해 클러스터를 구한다.
commonly used in recent papers, preferable approach
How to select $k$? Eigen gap이 가장 큰 $k$를 고른다.
\[ \Delta_k = |\lambda_k - \lambda_{k-1}| \]

'스터디 > 데이터사이언스' 카테고리의 다른 글
| [CS246] Flajolet-Martin (FM) Algorithm: Counting Distinct Elements from Data Stream (0) | 2023.12.22 |
|---|---|
| [CS246] Filtering Data Streams (0) | 2023.12.19 |
| [CS246] Gradient Boosted Decision Trees (GBDT) (0) | 2023.12.04 |
| [CS246] Sampling from a Data Stream (0) | 2023.12.04 |
| [CS246] Mining Data Streams (1) | 2023.12.03 |


