Motivation
실제 세계에서 데이터행렬(data matrix)은 매우 희소하다. (very sparse)
그러나 SVD로 분해하여 얻은 2개의 singular vector $U$, $V$는 sparse 하지 않다.
물론 $\Sigma$는 sparse하지만 $U$와 $V$에 비해 너무 크기가 작기 때문에 메모리 측면에서 별로 도움이 되지 않는다.
이런 이유로 행렬을 sparsity를 유지하면서 (의미있게) 분해할 필요가 있다.
CUR Decomposition
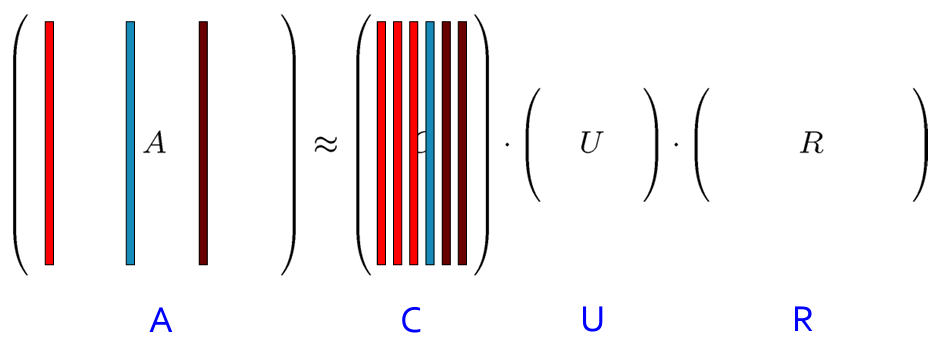
CUR 분해의 목표는 $\| M - CUR \|_F$ 의 값을 최소화 하는 것이다.
$C$는 column에서 랜덤하게 $r$개 뽑은 컬럼벡터, $R$은 row에서 랜덤하게 $r$개 뽑은 로우벡터가 된다.
$U$는 $C$와 $R$의 교집합으로 이루어진 정방행렬($W$)으로부터 계산된다. (아래에서 더 자세히 설명)

Choosing Rows and Columns
원래 데이터 행렬 $M$과 오차가 작아야 하므로, row와 column을 고를때 uniform하게 뽑지 않는다.
row/column의 importance(중요도)는 Frobenius norm의 제곱으로 정의한다.
그리고 각 row/column이 선택될 확률은 importance에 비례하도록 한다.
예를 들어, $[3, 4, 5]$의 중요도는 $3^2 + 4^2 + 5^2 = 50$이고, $[3, 0, 1]$의 중요도는 $3^2 + 0^2 + 1^1 = 10$이므로, 앞의 벡터가 5배 더 자주 선택되도록 한다.
$M$의 Frobenius norm을 $f$라 하자. ($f = \sum_{ij} m_{ij}^2$)
$p_i$와 $q_j$를 각각 $i$번째 row가 선택될 확률, $j$번재 column이 선택될 확률이라 하자. 그러면
\[ p_i = \cfrac{\sum_j m_{ij}^2}{f}, \quad q_j = \cfrac{\sum_i m_{ij}^2 }{f} \]
이다.
$j$번째 컬럼이 선택되었을 때, $j$번재 컬럼이 선택될 기대값의 제곱근으로 나누어서 저장한다. $r$개의 컬럼을 선택해야한다고 할 때, $j$번째 컬럼이 선택될 기댓값은 $rq_j$이므로, $M_j$의 값은 $\sqrt{rq_j}$로 나눈다.
$i$번째 row 역시 마찬가지로 $\sqrt{rp_i}$로 나누어서 저장된다.
Example: Choosing Rows and Columns

CUR 분해에 $r=2$를 이용한다고 하자. 먼저 $f = \| M \|_F^2 = 243$ 을 구한다.
이때 처음으로 Alien(2번째 컬럼, $q_2$), 두번째로 Casablanca를 선택(4번째 컬럼, $q_4$)했다고 하자.
각 컬럼이 선택될 확률을 $q_2,\ q_4$를 구하면 다음과 같다.
$q_2 = (1^2 + 3^2 + 4^2 + 5^2 + 0^2 + 0^2 + 0^2)/243 = 0.210$
$q_4 = (4^2 + 5^2 + 2^2)/243 = 0.185$
따라서 $C$의 첫번째 컬럼은 $[1,3,4,5,0,0,0]^\top$을 $\sqrt{rq_2} = \sqrt{2 \cdot 0.210} = 0.648$로 나눈 값이 된다. 즉 scaled Alien은 $[1.54, 4.63, 6.17, 7.72, 0, 0, 0]^\top$ 이 된다.
마찬가지로 $C$의 두번째 컬럼은 $[0,0,0,0,4,5,2]^\top$을 $\sqrt{rq_4} = \sqrt{2 \cdot 0.185} = 0.608$로 나눈 값이 된다. 즉 scaled Casablanca는 $[0,0,0,0,6.58, 8.22, 3.29]^\top$ 이 된다.
같은 과정으로 row에서 Jenny와 Jack이 순서대로 선택되었다고 하면 $R$ 행렬은 다음과 같다.
\[ R = \begin{bmatrix} 0 & 0 & 0 & 7.79 & 7.79 \\ 6.36 & 6.36 & 6.36 & 0 & 0 \end{bmatrix} \]
Computing the Middle Matrix $U$
$W$은 $C$와 $R$의 교집합 행렬이라 하자. 즉 shape는 $r \times r$ 이다.
※ Why the intersection? 교집합의 숫자들이 (절댓값이) 더 큰 값을 갖는다.

그리고 $W$를 SVD 분해를 한다. $W = XZY^\top$
그리고 $W$의 Moore-Penrose pseudoinverse $W^+$를 구하면 $W^+ = YZ^+ X^\top$ 이다.
마지막으로 $U=Y(Z^+)^2 X^\top$ 을 계산한다.
- $W^{-1} = (Y^\top)^{-1} Z^{-1} X^{-1}$
- $X$와 $Y$는 orthonormal이므로 $X^{-1} = X^\top,\ Y^{-1}=Y^\top$ 이다.
- $Z$는 대각행렬이므로 $Z^{-1} = \text{diag}(1/Z_{ii})$ 이다.
- $W$가 nonsingular하다면 pseudoinverse는 true inverse 이다.
Example: Computing the Middle Matrix
위의 예시에 이어서 컬럼은 Alien, Casablanca 순서로, row는 Jenny, Jack 순서로 선택되었다고 하자.
그러면
\[ W = \begin{bmatrix} 0 & 5 \\ 5 & 0 \end{bmatrix} \]
이다.
$W$를 SVD 분해하면 다음과 같다.
\[ W = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 5 & 0 \\ 0 & 5 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \]
여기서 $\Sigma^+$를 구하면 $\Sigma^+ = \begin{bmatrix} 1/5 & 0 \\ 0 & 1/5 \end{bmatrix}$ 이므로
\[ U = Y (\Sigma^+)^2 X^\top = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1/5 & 0 \\ 0 & 1/5 \end{bmatrix} ^2 \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 1/25 \\ 1/25 & 0 \end{bmatrix} \]
따라서 최종적으로 얻은 CUR은 다음과 같다.
\begin{align} CUR &= \begin{bmatrix} 1.54 & 0 \\ 4.63 & 0 \\ 6.17 & 0 \\ 7.72 & 0 \\ 0 & 6.58 \\ 0 & 8.22 \\ 0 & 3.29 \end{bmatrix} \begin{bmatrix} 0 & 1/25 \\ 1/25 & 0 \end{bmatrix} \begin{bmatrix} 0 & 0 & 0 & 7.79 & 7.79 \\ 6.36 & 6.36 & 6.36 & 0 & 0 \end{bmatrix} \\ &= \begin{bmatrix} 0.39 & 0.39 & 0.39 & 0 & 0 \\ 1.18 & 1.18 & 1.18 & 0 & 0 \\ 1.57 & 1.57 & 1.57 & 0 & 0 \\ 1.96 & 1.96 & 1.96 & 0 & 0 \\ 0 & 0 & 0 & 2.05 & 2.05 \\ 0 & 0 & 0 & 2.56 & 2.56 \\ 0 & 0 & 0 & 1.02 & 1.02 \end{bmatrix} \end{align}
※ 원래 데이터 행렬 $M$과 상당히 다르게 보이는데, 그 이유는 (1) row와 column이 확률에 비례하게 랜덤하게 고른 것이 아니라 임의로 선택했고 (2) $r$의 값이 작기 때문이다.
SVD vs CUR
만약 데이터가 2개의 cloud로 형성되어 있다고 하자.
SVD의 차원(축)은 두 cloud의 분산을 고려하기 때문에 두 데이터 cloud 사이에 위치하지만, CUR은 그렇지 않다.

'스터디 > 데이터사이언스' 카테고리의 다른 글
| [CS246] RecSys (2) - Content-based Approach (0) | 2023.10.13 |
|---|---|
| [CS246] RecSys (1) - Introduction (0) | 2023.10.12 |
| [CS246] Dimensionality Reduction (3) - SVD (0) | 2023.10.10 |
| [CS246] Dimensionality Reduction (2) - PCA (0) | 2023.10.08 |
| [CS246] Dimensionality Reduction (1) - Introduction (0) | 2023.10.07 |



