[CS246] Finding Similar Items (5) - LSH Family

 

Locality-Sensitive Family

Meanings of Sensitivity Values

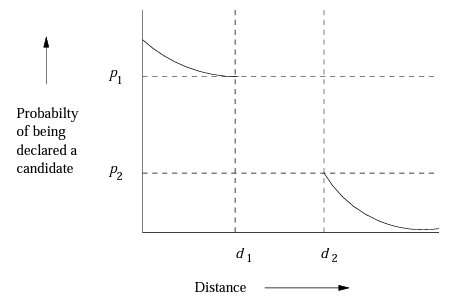
family of $F$ of function은 다음을 만족하면 $(d_1, d_2, p_1, p_2)$-sensitive라고 부른다.

• 모든 함수 $f \in F$와 점 $x,y$에 대하여 
  • $d(x,y) \le d_1$이면, $f(x)=f(y)$일 확률은 최소 $p_1$이다.
  • $d(x,y) \ge d_1$이면, $f(x)=f(y)$일 확률은 최대 $p_2$이다.

Behavior of a $(d_1,d_2, p_1, p_2)$-sensitive function

$d$가 Jaccard distance라면 $d = 1-\text{sim}(x,y)$이므로

$d(x,y) \le d_1 \Rightarrow 1 - \text{sim}(x, y) \le d_1 \Rightarrow 1 - d_1 \le \text{sim}(x,y)$

$d(x,y) \ge d_ 2\Rightarrow 1 - \text{sim}(x, y) \ge d_2 \Rightarrow 1 - d_2 \ge \text{sim}(x,y)$ 이다.

그런데 Jaccard similarity는 곧 minhash 값이 같을 확률과 같으므로 minhashing의 경우 $(d_1, d_2, 1-d_1, 1-d_2)$-sensitive family 이다. (단, $d_1 < d_2$)

 

Amplifying an LSH Family

앞서 band를 이용한 테크닉을 더 일반화하여 S-curve를 더 효과적으로 만들어보자.

AND는 band 내의 row에 적용되고, OR은 many band에 적용된다.

 

AND-construction of F

아래 두 조건을 만족하면 $F'$은 $(d_1, d_2, p_1^r, p_2^r)$-sensitive 라고 한다.

• $F'$의 $f$가 $f \in \{ f_1, \dots, f_r \}$ 이고
• $f(x)=f(y) \text{ iff } f_i(x)=f_i(y) \text{ for all } i=1, 2, \dots, r$

AND-construction은 확률을 작게한다. $r$값을 잘 조정하면 $p_2$는 $0$에 가까이 감소시킬 수 있으면서 $p_1$은 $0$과 충분히 떨어져 있을 수 있다.

OR-construction of F

아래 두 조건을 만족하면 $F'$은 $(d_1, d_2, 1-(1-p_1)^b, 1-(1-p_2)^b)$-sensitive 라고 한다.

• $F'$의 $f$가 $f \in \{ f_1, \dots, f_b \}$ 이고
• $f(x)=f(y) \text{ iff } f_i(x)=f_i(y) \text{ for one or more values of } i=1, 2, \dots, b$

AND-construction은 확률을 크게한다. $b$값을 잘 조정하면 $p_1$는 $1$에 가까이 증가시킬 수 있으면서 $p_2$은 $0$과 충분히 가까이 할을 수 있다.

 

AND-OR Composition

확률 $p$는 $1-(1-p^r)^b$로 변환된다. 

$F$가 minhash function이고, $(0.2, 0.6, 0.8, 0.4)$-sensitivity family라 하자.

$F_2$를 $f_1$으로부터 $r=4$로 얻은 AND-construction이리고, $F_3$을 $F_2$로부터 $b=4$인 OR-construction이라 하자. 그러면 $p$는 $1-(1-p^4)^4$가 된다.

Example: AND-OR Composition (Stanford CS246)

OR-AND Composition

확률 $p$는 $(1-(1-p)^b)^r$로 변환된다.

$F$가 minhash function이고, $(0.2, 0.6, 0.8, 0.4)$-sensitivity family라 하자.

$F_2$를 $F_1$으로부터 $b=4$로 얻은 OR-construction이리고, $F_3$을 $F_2$로부터 $r=4$인 AND-construction이라 하자. 그러면 $p$는 $(1-(1-p)^4)^4$가 된다.

Example: OR-AND Composition (Stanford CS246)

Cascading Constructions

(4,4) OR-AND 를 하고 이어서 (4,4) AND-OR을 적용하면 (0.2, 0.8, 0.8, 0.2)-sensitivity family는 (0.2, 0.8, 0.9999.., 0.0008715)-sensitive family가 된다. (대신에 signature길이는 256이어야 한다.)