Recap: A-Priori
A-Priori 알고리즘은 2-pass 알고리즘이다. pass1에서는 아이템을 스캔하여 개수를 저장하고, pass2에서 candidate frequent pairs ($C_2$)를 찾는다. 각 $C_k$로부터 truly frequent itemsets $L_k$를 찾는 과정을 반복한다.
이렇게 크기가 $k$인 frequent itemsets $L_k$를 통해 association rule을 찾을 수 있다.
그러나 $C_2$ 역시 너무 커서 main memory에 들어가지 않으면?
이 문제를 해결하는 알고리즘이 PCY, multistage, multihash 이다.
PCY Algorithm
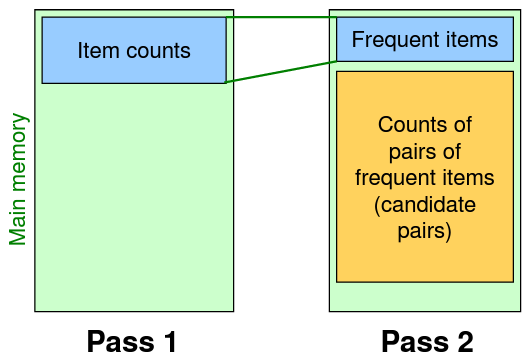
A-Priori의 pass1에서 사용되지 않는 main-memory가 너무 많다. 이렇게 사용되지 않는 main memory의 공간을 활용하여 frequent하지 않을 아이템을 최대한 제거하는 알고리즘이다.
이 주어진 공간을 해시테이블로 만들어 item pair의 빈도수를 저장하는 것이다.
PCY - Pass 1
main memory에 해시테이블을 만든다. (최대한 많은 bucket을 만든다)
bucket은 pair의 개수를 의미한다. item pair가 해싱되어 해당 bucket의 값(count)를 증가시킨다.

PCY - Pass 2
frequent bucket에 있는 pair만 candidate itemsets으로 한다. (truly frequent itemset을 구하기 위해서 support filtering이 필요하다. 이는 후술할 multistage, multihash에서도 마찬가지이다.)
Why PCY works?
PCY알고리즘이 실제 동작하는 원리를 알아보자.
toy example로 5개의 pair, support=3이고 해시테이블은 3개의 bucket ($B_1, B_2, B_3$)을 갖는다고 하자.
pair 중에서 실제 count는 $p_1=3,\ p_2=1,\ p_3=1,\ p_4=1,\ p_5=5$라 하자. ($p_1,\ p_5$만 실제로 frequent pair이다)
그리고 $p_1,\ p_2$는 $B_1$에, $p_3,\ p_4$는 $B_2$, 그리고 $p_5$는 $B_3$으로 각각 해싱된다고 하자.
그러면 각 bucket의 count는 $B_1=4,\ B_2=2,\ B_3=5$가 된다.
pass2에서 $B_1,\ B_3$에 있는 pair만 candidate set $C_2$로 구성하면 된다. (A-priori보다 훨씬 적을 것이다)
toy example을 통해, truly frequent pair는 bucket에 포함되자마자 support를 만족하기 때문에 해당 bucket은 truly frequent pair를 놓치지 않는다. ($B_1,\ B_3$)
반대(대우?)로 bucket count가 support보다 작으면 해당 bucket에 포함된 pair들은 support를 넘지 못하기 때문에 infrequent함을 알 수 있다. ($B_2$)
물론, infrequent pair 역시 frequent pair와 동일한 bucket에 해싱될 수 있다. ($B_1$의 $p_2$). 이는 $L_2$를 만들때 필터링될 때 걸러진다.
Bit-vector: Replacement of Buckets
최대한 infrequent pair가 frequent bucket에 해싱되지 않도록 (즉 해시충돌이 적게 일어나도록) 하려면 bucket의 수를 최대한 많이 늘려야한다. 일반적인 해시테이블처럼 정수로 표현하면 4바이트(32비트 기준)를 차지하게 된다. 그러나 우리는 해당 bucket이 frequent/infrequent 한지(support를 넘는지 안넘는지)만 볼 것이므로 4바이트를 차지할 이유가 없다. (어차피 해당 bucket에 truly frequent pair가 해당되면 bucket은 이미 support를 만족함) 그래서 bucket에 integer가 아니라 비트맵(혹은 bit-vector)를 이용하여 메모리를 더 적게 차지한다. (약 $1/32$배)
또한 pass2에서 비트벡터가 1인 bucket만 고르면 되므로 구현이 간단하다.

※ pass2 에서 더이상 triangular matrix는 사용하지 않는다. 즉 triple (item, item, count)을 사용한다.
Multistage Algorithm: Extension of PCY
※ frequent itemsets모두 해당되는 이야기이지만 메모리 이슈의 대부분을 차지하는 frequent pair에 대해서 다룬다
PCY에서 해시테이블을 통해 우리는 A-priori에서보다 candiate pair의 크기를 더 줄일 수 있었다.
candidate pair를 줄이는 방법은 최대한 truly frequent pair만 걸러내는 것이다.
PCY의 pass 1으로 얻은 frequent bucket에는 false positive가 존재한다. 이제 이 false positive를 최대한 줄여보자.
Multistage 알고리즘은 이런 이유로 pass 3을 도입한다.
pass 1은 PCY의 pass1과 같이 해시테이블을 이용하여 frequent bucket을 bitmap으로 저장한다.
그리고 바로 candidate pair를 구성하는 것이 아니라 두번째 해시테이블을 만들어 두번째 bitmap을 만든다.
이렇게 얻은 2개의 bitmap을 이용하여 candidate pair를 구한다. (구체적 언급은 되지 않았지만, AND bit연산을 이용하여 빠르게 구할 수 있을 것이다.)
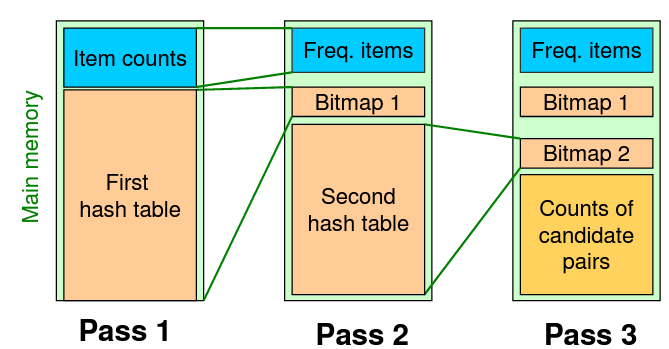
pass1과 pass2의 두 해시함수는 반드시 독립(independent)이어야 한다. (false positive sample이) 첫번째 해시로 frequent하다고 해도, 두번째 해시에서는 infrequent해야하기 때문이다.
Multihash Algorithm: Another extension of PCY
Multihash 알고리즘은 pass1에 두개의 해시테이블(그리고 두개의 해시함수)을 이용하여 한번에 두개의 비트맵(비트벡터)를 만들어 candidate pair를 만드는 방법이다.
Risk: 해시테이블의 bucket의 수가 절반이 되므로 각 bucket의 평균 count는 2배가 될 위험이 있다.

여담
아마 이 논문을 참고한 것으로 보인다.
An Effective Hash-Based Algorithm for Mining Association Rules (Jong Soo Park, Ming-Syan Chen, Philip S. Yu)
https://dl.acm.org/doi/abs/10.1145/568271.223813
이 논문을 쓰신 Yu 교수님은 현재도 University of Illiois Chicago 컴퓨터공학 교수하고 계신다.
'스터디 > 데이터사이언스' 카테고리의 다른 글
| [CS246] Finding Similar Items (1) - Introduction (0) | 2023.09.18 |
|---|---|
| [CS246] Frequent Itemsets: SON, Toivonen Algorithm (0) | 2023.09.15 |
| [CS246] A-Priori Algorithm: Finding Frequent Itemsets (0) | 2023.09.12 |
| [CS246] Frequent Itemsets Mining & Association Rules (0) | 2023.09.11 |
| [CS246] Spark: Extends MapReduce (0) | 2023.09.09 |



