[CS224w] Theory of GNNs (2) - Neighbor Aggregation, GIN (Graph Isomorphism Network)

 

전 포스팅에서는 GNN의 node embedding이 왜 표현력이 좋은지 omputational graph의 관점에서 설명했다.

이번에는 neighbor aggregation의 관점에서 더 살펴보자.

 

Neighbor Aggregation

Neighbor aggregation은 multi-set function과 동일한 구조를 갖는 것에서 시작한다.

aggregation function으로 GCN (ICLR 2017)에서는 mean-pool, GraphSAGE (NeurIPS)에서 max-pool을 제안하였다.

GCN에서는 $\text{Mean}(\{ x_u \}_{u \in N(v)})$

GraphSAGE에서는 $\text{Max}(\{ x_u \}_{u \in N(v)})$

GCN (mean-pool) [ICLR 2017]

element-wise mean을 계산하고, activation function으로 linear/ReLU 등을 통과시킨다.

그러나 GCN의 aggregation function은 서로 다른 multi-set을 구별하지 못할 수 있음이 제기되었다. [ICLR 2019]

Failure case illustration of GCN

GraphSAGE (max-pool) [NeurIPS 2017]

GraphSAGE의 aggregation function (max-pooling) 역시 서로 다른 multi-set을 구별하지 못한다.

Failure case illustration of GraphSAGE

source: How Powerful Are Graph Neural Networks? [ICLR 2019]

중간 요약

GNN의 표현력은 neighbor aggretation function에 달려있다. 그리고 neighbor aggregation은 multi-set을 리턴하는 함수이다. 그러나 GCN와 GraphSAGE에서 사용되는 mean-pool 또는 max-pool은 그렇지 못하다. GCN과 GraphSAGE는 GNN의 최대 표현이 아니다. (not maximally powerful GNNs)

 

따라서 우리는 injective multiset function을 디자인해야한다.

반응형

Injective Multi-Set Function

모든 injective multi-set function은 아래와 같이 표현된다.

Universal Approximation Theorem [Hornok et al. 1989]

hidden layer 차원이 충분히 크고 activation function으로 비선형 함수 $\sigma(\cdot)$를 갖는 1-hidden-layer MLP은 거의 모든 임의의 함수(어떤 함수든)를 근사할 수 있다. 

Note: 무수히 많은 짧은 구간으로 나눈 후, 각 구간마다 sigmoid의 상수배와 덧셈을 적당히 조작하여 함수를 근사할 수 있다. (엄밀한 증명 생략)

이 이론을 이용하여 우리는 MLP를 이용하여 injective multiset function을 만들 것이다. (실제로 hidden dimension은 100~500이면 충분하다고 한다.)

Injective Multi-Set Function of Neural Network

Graph Isomorphism Network (GIN) [ICLR 2019]

GIN의 neighbor aggregation function은 위의 MLP로 만들어서 어떠한 경우에도 aggregation이 실패하는 경우가 없게 하였다. 따라서 GIN은 이전까지 소개한 message-passing GNN 중에서 most expressive GNN이다.

Relation to WL Graph Kernel

Color refinement algorithm in WL kernel

(1) 모든 노드 $v$에 대하여 initial color $c^{(0)}(v)$
(2) 반복적으로 node color를 refine
\[ c^{(k+1)}(v) = \text{HASH} \left( c^{(k)}(v), \{ c^{(k)}(u) \}_{u \in N(v)} \right) \]
(3) $K$ step 이후의 color refinement는 $c^{(K)}(v)$

두 그래프의 노드 색깔 집합 (set of colors)가 같다면 두 그래프는 동형(isomorphic)이다. 

GIN은 injective HASH function으로 neural network를 이용한다

특히, 우리는 injective function을 tuple의 형태로 모델링할 것이다.

최종적으로 모델링한 injective function은 다음과 같다. ($\epsilon$은 learnable 상수이다.)

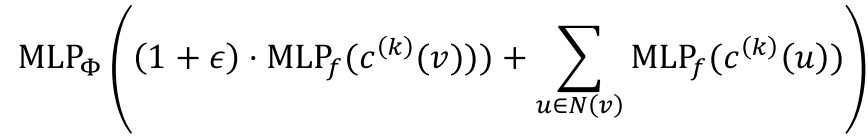
The Complete GIN Model

input feature $c^{(0)}(v)$는 one-hot으로 표현하고, 직접 합계를 계산한다. (direct summation is injective)

GINConv maps different inputs to different embeddings

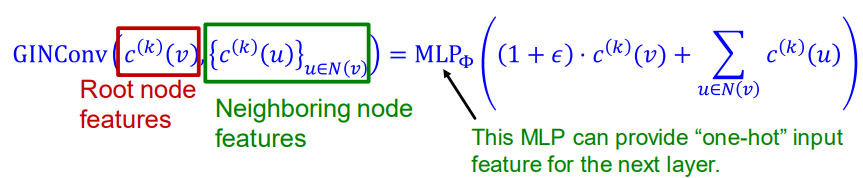
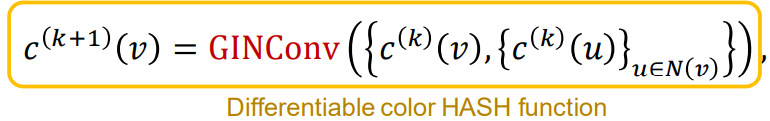
GIN and WL Graph Kernel

GIN은 WL Graph Kernel의 미분가능한 신경망 버전으로 생각할 수 있다.

(GIN can be understood as differentiable neural version of the WL graph kernel)

GIN이 WL graph kernel보다 장점인 점은

(1) 노드 임베딩이 저차원이 가능하므로 fine-grained 작업에 효율적이다.

(2) update function의 파라미터가 learnable하므로 downstream task에 적용가능하다.

Note: (Classification에서) Coarse-grained는 종의 분류라면, Fine-grained는 개의 품종을 분류하는 것으로 비유할 수 있다.

 

두 그래프가 GIN으로 구별 가능하다면(can be distinguished), 두 그래프 역시 WL kernel로도 구별할 수 있다. 그리고 그 역도 가능하다.

따라서 GIN은 대부분의 현실 그래프들을 구별하는데 powerful하다.