
Normal Distribution Theory
정규분포를 따르는 2개의 확률변수의 합은 정규분포임을 알 수 있었다.
이제 이를 확장해서
개의 확률변수 의 합을 라 하면
Proof
mgf를 이용하여 증명한다.
확률변수의 합의 mgf는 각 확률변수의 mgf의 곱과 같으므로
Zero covariance is equivalent to independence
Proof
새로운 확률변수
한편, 공분산은
두 벡터 V, W가 독립이면
이는 (
The Chi-squared Distribution
이 의 i.i.d라 할 때 이라 하면
이다. 이 때은 카이제곱분포의 자유도(degrees of freedom)이라 한다.
카이제곱분포의 기댓값과 분산
카이제곱분포의 합
독립인 두 확률변수
독립인 두 카이제곱분포의 확률변수의 합은 자유도의 합과 같다. 즉
표본평균과 표본분산
이 의 i.i.d라 할 때 표본평균과 표본분산을 각각 이라 하고
그리고 아래 두가지를 만족한다.
Why
https://www2.stat.duke.edu/courses/Fall18/sta611.01/Lecture/lec12_mean_var_indep.pdf
https://trivia-starage.tistory.com/250
표본분산은 왜 n-1로 나눌까? (불편추정량, 자유도)
표본분산은 왜 n이 아니라 n-1로 나눌까?Notation
trivia-starage.tistory.com
표본 분산
따라서
Chapter 5에 나오지만, 위 성질 때문에
The
이고 이고 라고 하자. 그러면
이다.
Note: 독립 조건이 필요하다.

Example
i.i.d인
그러면
표본평균과
i.i.d인
따라서
The
두 카이제곱 확률변수과 이고 이라 하면
이다.
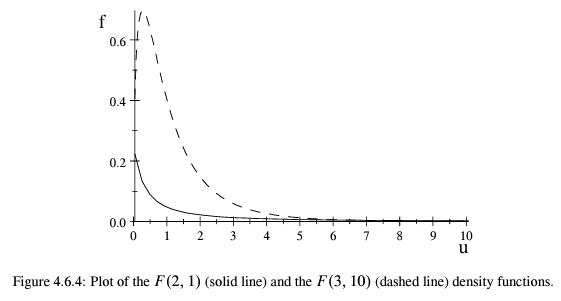
만약
proof



