Why sampling is important?
bayesian inference는 기댓값은 계산하는 방법이다. (discrete한 경우엔 적분이 아니라 합계가 된다.)
\[ \mathbb{E}_{p(\theta | X)}[f(\theta)] = \int f(\theta) p(\theta | X) d\theta \]
그러나 위 정의대로 정확히 계산하는 것은 불가능(exact inference is intractable)한 경우가 많기 때문에, 우리는 Monte Carlo method를 이용하여 기댓값을 근사한다.
\[ \mathbb{E}_{p(\theta | X)}[f(\theta)] \approx \cfrac{1}{m}\sum_{s=1}^{m}f(\theta_s), \quad \theta_1, \dots \theta_m \overset{\text{i.i.d.}}{\sim} p(\theta | X) \]
Monte Carlo 식을 살펴보면, 우리는 $\theta_i$를 $p(\theta | X)$로부터 sampling을 해야한다.
심지어 $p(\theta | X)$를 모르는 경우가 대부분이다!
Sampling methods for elementary distributions
대부분의 프로그래밍 언어 라이브러리나 패키지에는 기본적인 분포의 샘플링 코드가 제공되어있다.
대부분 uniform distribution으로부터 샘플링하는 것을 기초로 한다.
Uniform distribution
uniform random variable은 다음과 같이 구한다.
\[ x = \cfrac{\text{RNG()}}{\text{RNG}_{\text{MAX}}} \overset{d}{=} \text{Unif}(0, 1) \]
즉, 임의의 구간 $(a,b)$에서 uniformly sampling은 다음과 같이 구한다.
\[ x_0 \sim \text{Unif}(0,1),\ x = a + (b-a)x+0,\ x \overset{d}{=}\text{Unif}(a,b) \]
Gaussiasn distribution
가우시안 분포로부터 샘플링하는 알고리즘은 다양하다. 이번 포스트에서는 box-muller 알고리즘만 소개한다.
Box-Muller Algorithm
while True do
Sample $z_1 \sim \text{Unif}(-1, 1)$ and $z_2 \sim \text{Unif}(-1, 1)$
if $z_1^2 + z_2^2 \le 1$ then
Break
end if
end while
Return $x = z_1 \sqrt{(-2\log (z_1^2 + z_2^2)) / (z_1^2 + z_2^2) }$
이렇게 얻은 $x$ 표준정규분포를 따른다. 즉 $x \sim \mathcal{N}(0, 1)$
만약 $\mu, sigma$를 따르게 하고 싶다면 scaling을 하면 된다.
\[ x=\mu + \sigma \epsilon, \quad \epsilon \sim \mathcal{N}(0, 1) \]
multivariate Gaussian으로 sampling하려면 다음과 같다.
\[ x = \mu + L \epsilon,\ (\epsilon_1, \dots, \epsilon_d) \overset{\text{i.i.d.}}{\sim} \mathcal{N}(0, 1),\ \Sigma=LL^\top \]
$L$은 공분산행렬을 촐레스키 분해한 것이다.
Categorical distribution
$k$개의 category가 각각 $\theta$의 확률을 갖는다 하자. 즉 $\theta \in [0, 1]^k$ with $\sum_j \theta_j = 1$
이때 categorical distribution은 다음과 같이 정의한다.
\[ p(x|\theta) \sim \text{Cat}(\theta) \Rightarrow p(x=j) = \theta_j \]
이제 categorical distribution을 샘플링해보자.
Sampling from $\text{Cat}(\theta)$
$\tilde{\theta}$를 누적확률이라 하자. 즉 $\tilde{\theta}_j$는 $j$번째 index 까지의 $\theta$ 누적값이다.
$u \sim \text{Unif}(0, 1)$, $x=1$
while $u > \tilde{\theta}_x$ do
$x \leftarrow x+1$
end while
Return $x$
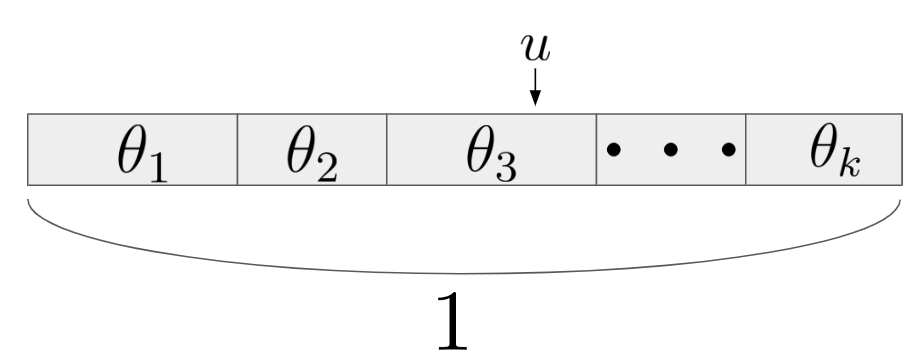
예를 들어, 실제 샘플링된 값이 $\theta_3$ 라 하자. 그러면 $x=1, 2$까지는 $u > theta_1$, $u > \theta_1 + \theta_2$이므로 $x$값을 증가시키고, $x=3$일 때, $u < \theta_1 + \theta_2 + \theta_3$이므로 $x=3$을 반환한다.
naive하게 $\mathcal{O}(k)$의 시간복잡도를 갖고, 이진탐색 등의 알고리즘을 적용하면 $\mathcal{O}(\log k)$ 로 더 빠르게 찾을 수 있다.
Poisson distribution
포아송분포는 비모수 베이지안 모델링에서 자주 사용되므로 간단히 소개한다.
아래 알고리즘은 단순하지만 꽤 비효율적이다. (프로그램 언어 패키지 내부적으로는 효율적으로 구현되어있다.)
Sampling from Poisson distribution $\text{Poisson}(\lambda)$
$x=0$, 그리고 $t \sim \text{Unif}(0, 1)$
while $t > e^{-\lambda}$ do
$x \leftarrow x + 1$
$t \leftarrow t \cdot u$ where $u \sim \text{Unif}(0, 1)$
end while
Return $x$
Gamma, Beta, Dirichlet distribution
대부분의 scientific programming language에는 unit Gamma $\text{Gamma}(a, 1)$을 이용하여 샘플링한다.
감마함수의 샘플링 역시 다양한 방법이 있지만, 여기서는 간단한 버전만 다룬다.
Sampling from Gamma distribution
\[ x' \sim \text{Gamma}(a,1), \quad x:= \cfrac{x'}{b} \overset{d}{=} \text{Gamma}(a,b) \]
Sampling from Beta distribution
\[ x \sim \text{Gamma}(a),\ y \sim \text{Gamma}(b), \quad z:=\cfrac{x}{x+y} \overset{d}{=} \text{Beta}(a,b) \]
Sampling from Dirichlet distribution
\[ x_j \sim \text{Gamma}(\alpha_j, 1) \text{ for } j=1, \dots, k \]
\[ z:= \left[ \cfrac{x_1}{\sum_j x_j}, \dots, \cfrac{x_k}{\sum_j x_j} \right] \overset{d}{=} \text{Dir}(\alpha) \]
Inverse CDF method
inverse CDF method, inverse transform sampling 등으로 불린다.
기초 통계학에서 배우는 그 방법이고, 누적분포함수 $F$의 역함수 $F^{-1}$이 계산가능할 때 적용할 수 있다.
$u \sim \text{Unif}(0, 1)$일 때,
\[ \mathbb{P}(F_x^{-1}(u) \le y) = \mathbb{P}(u \le F_x(y)) = F_x(y) \]
※ $F_x^{-1}$은 $x$의 quantile 이라고도 부른다.
Example of Inverse CDF method: exponential distribution
지수분포의 PDF는 $f(x|\lambda) = \lambda e^{-\lambda x}$이고, CDF는 $F(x) = 1 - e^{-\lambda x}$ 이다.
따라서
\[ F_x(y) = 1 - e^{-\lambda y}, \quad F_x^{-1}=-\cfrac{\log (1-u)}{\lambda} \]
$u \overset{d}{=} 1-u$임을 이용하면
\[ u \text{Unif}(0, 1), \quad x:= -\cfrac{\log u}{\lambda} \overset{d}{=} \text{Exp}(\lambda) \]
'스터디 > 확률과 통계' 카테고리의 다른 글
| [Sampling] Importance Sampling (0) | 2023.09.27 |
|---|---|
| [Sampling] Rejection Sampling (0) | 2023.09.26 |
| Measure Theoretic Probability (4) | 2023.09.06 |
| UMVUE (Uniformly Minimum Variance Unbiased Estimator) (0) | 2023.05.31 |
| Bootstrapping (0) | 2023.05.30 |

